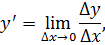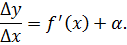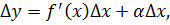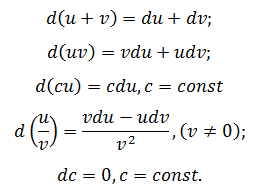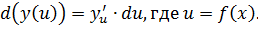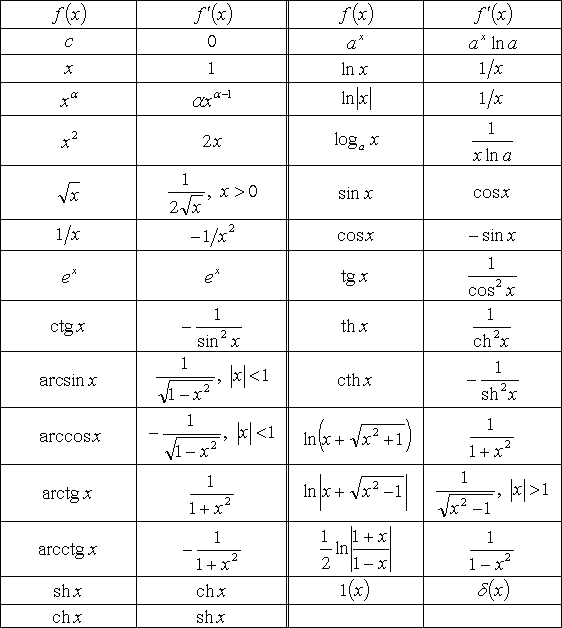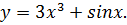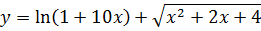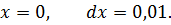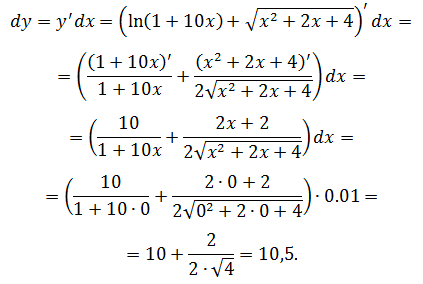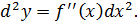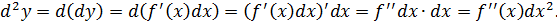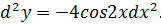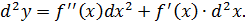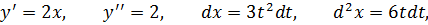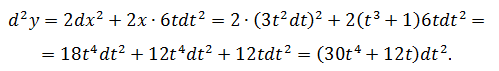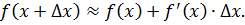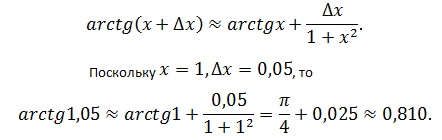дифференцировать функцию что значит

Дифференцирование функции, нахождение производной

Если вам нужно решить задачу, в рамках которой требуется вычислить производную какой-либо функции с одной переменной, советуем внимательно прочесть эту статью. Здесь приводятся общие положения теории дифференцирования, имеющие отношение к вычислению производной. Для этого могут быть использованы разные способы, ведь исходная функция может быть задана явно или неявно, в параметрическом виде, быть элементарной, основной или сложной, значит, в каждой ситуации бывает нужен свой подход.

Таблица дифференцирования функции

Мы собрали всю информацию, которую нужно знать для правильного дифференцирования функции, и представили ее в табличном виде:

Степенная фунция y = x p

y = a x a x ‘ = a x · ln a

В частности, при a = e имеем

log a x ‘ = 1 x · ln a

В частности, при a = e имеем

y = ln x ln x ‘ = 1 x

Производная сложной функции

( f ( g ( x ) ) ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x )

Производная неявно заданной функции

Производная обратной функции

Обратные тригонометрические функции

Производная параметрически заданной функции

y = f ( x ) y ‘ = y · ( ln ( f ( x ) ) ) ‘

Пояснения таблицы

Содержимое таблицы требует небольших пояснений. Например, в наиболее простом случае для дифференцирования нам пригодится определение производной, т.е. вычисление соответствующего предела. Это действие носит название непосредственного дифференцирования.

Если вам приходится работать с основной элементарной функцией, то следует использовать таблицу основных производных. В ней приводятся все готовые значения, доказанные на основании определения. Это очень удобно, и мы советуем вам держать такую таблицу под рукой.

Источник

Дифференцировать функцию что значит

При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.

Производной функции y = f ( x ) по переменной x в некоторой точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, то есть

Производная характеризует скорость изменения функции в достаточно малой окрестности заданной точки.

Приведем таблицу производных основных элементарных функций (без доказательства), которые рассматриваются нами как функции простые и явно заданные.

Следствие. В точках разрыва функция производной не имеет

Существуют такие точки, в которых функция непрерывна, но не дифференцируема. Так, функция y =| x | в точке x =0 непрерывна, но производной не имеет, так как в этой точке к графику функции можно провести бесконечное множество касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к теореме 3.9 неверно.

Среди явных функций особое место занимают обратные функции, производная которых находится с помощью следующей теоремы.

Теорема 3.10. Если строго монотонная функция y = f ( x ) дифференцируема на некотором интервале Х, причем ее производная не обращается в нуль на Х, то обратная к ней функция x = φ ( y ) также дифференцируема на этом интервале, при этом:

По определению производной можно записать:

Среди явных функций выделяют класс сложных функций.

Теорема 3.11. Чтобы продифференцировать сложную функцию необходимо сначала продифференцировать внешнюю функцию по внутренней, считая внутреннюю функцию независимой переменной, затем продифференцировать внутреннюю функцию по независимому переменному и результаты дифференцирования перемножить, то есть

Решение. Согласно формуле (3.31) и с учетом табли чных формул (3.17), (3.19), (3.29) имеем:

где t – параметр. Производную такой функции несложно получить:

Пример 3.9. Найти производную функции .

Решение. Согласно формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:

Помимо таблицы производных имеют место правила дифференцирования.

Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме производных этих функций:

Данная теорема может быть обобщена для произвольного конечного числа функций-слагаемых.

Решение. Согласно формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:

Теорема 3.13. Производная произведения двух дифференцируемых функций равна произведению производной первой функции-сомножителя на вторую функцию плюс произведение первой функции на производную второй функции–сомножителя, то есть

Решение. Согласно формуле (3.34) и с учетом табличных формул (3.22), (3.24) имеем:

Теорема 3.14. Производная частного двух функций равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть

Решение. Согласно формуле (3.35) и с учетом табличных формул (3.17), (3.29) имеем:

Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной произведения, с учетом табличных формул (3.17) и (3.18) имеем:

Дифференциалом функции y = f ( x ) в точке x называется главная часть приращения этой функции, равная произведению производной функции на приращение аргумента:

Формула (3.39) применяется для вычисления приближенных значений функций.

Источник

Дифференцируемая функция

Из Википедии — свободной энциклопедии

Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках.

Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется её дифференциалом (в данной точке).

Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке. [1]

В случае функции комплексной переменной дифференцируемость в точке часто называется моногенностью и существенно отличается от понятия дифференцируемости в вещественном случае. Ключевую роль в этом играет так называемое условие Коши — Римана. Функция, моногенная в окрестности точки, называется голоморфной в этой точке. [2] [3]

В функциональном анализе существует обобщение понятия дифференцирования на случай отображений бесконечномерных пространств — производные Гато и Фреше.

Обобщением понятия дифференцируемой функции являются понятия субдифференцируемых, супердифференцируемых и квазидифференцируемых функций.

Источник

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

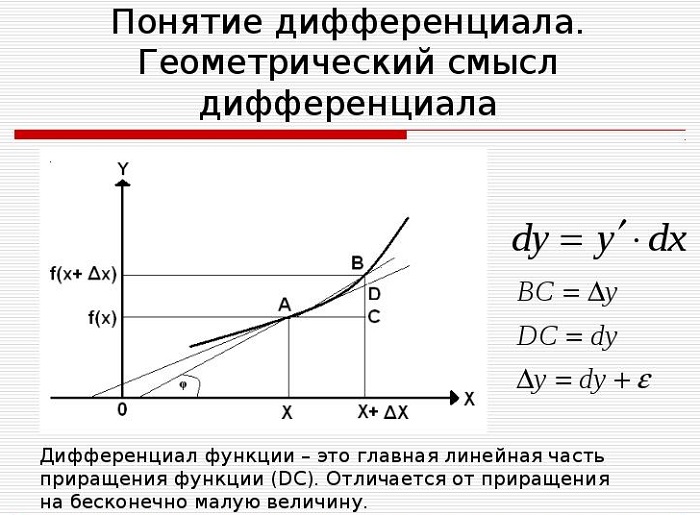
Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Заключение

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник

11. Дифференцируемость функции в точке. Функции, дифференцируемые на интервале и их свойства: Теоремы, Роля, Лагранжа.

Дифференцируемость функции в точке

Пусть функция y=f(x) определена на интервале (a,b), x-некоторая фиксированное значение аргумента из указанного интервала, x-любое приращение аргумента.

Теорема. Для того чтобы функция y=f(x) являлась дифференцируемой в данной точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Док-во: 1) Необходимость: пусть функция y=f(x) дифференцируема в данной точке x, то есть ее приращение y в этой точке представимо в виде y=Ax + x. Предположив, что x#0 поделим это равенство на x. Получим =A+. Из этого равенства вытекает существование производной, т.е.lim(x0)=A

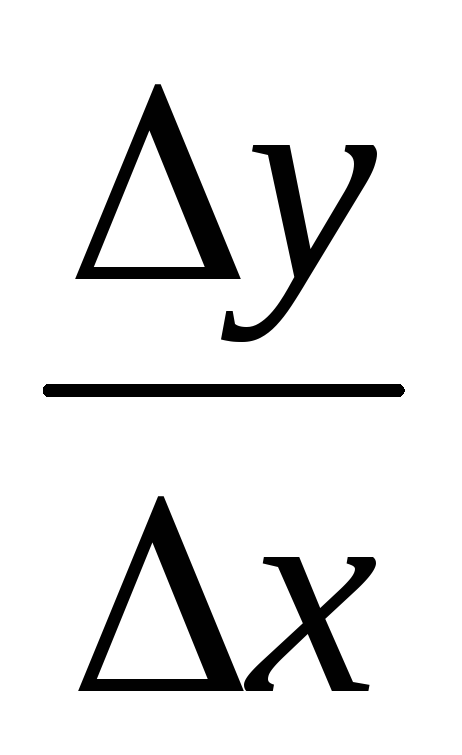
2) Достаточность: пусть функция y=f(x) имеет в данной точке x конечную производную, т.е. существует предельное значение lim(x0) =f ’(x)

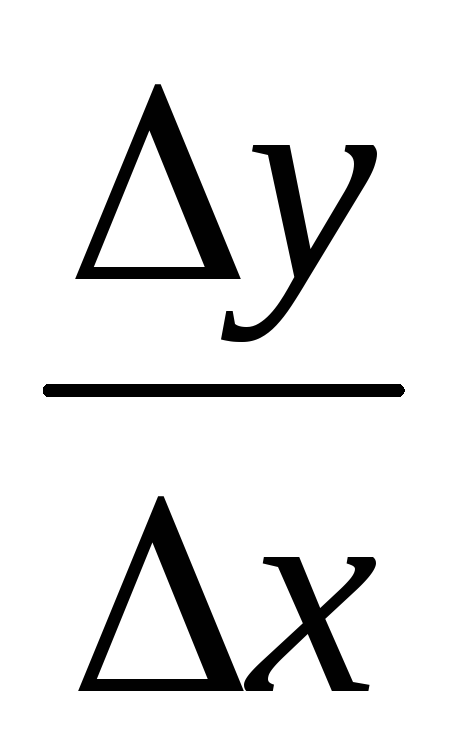
В силу определения предельного значения функция =-f’’(x) аргумента x является бесконечно малой при x0, т.е. y= f’’(x) x +x, где lim(x0)=0. Это представление совпадает с представлениемy=Ax + x, если обозначать через А не зависящее от x число f’’(x). Т.е. функция y=f(x) дифференцируема в точке x.

Теорема. Если каждая из функций u(x) и v(x) дифференцируема в данной точке x, то сумма, разность, произведение и частное этих функций также дифференцируемы в этой точке:

[ u(x) ]’ = u’(x)v’(x),

Опр. Функция y=f(x) называется дифференцируемой на интервале, если она дифференцируема во всех внутренних точках этого интервала.

Теорема Ферма. Если функция y=f(x) дифференцируема в точке c и имеет в этой точке локальный экстремум, то f ’(c)=0.

Опр. локального max(min): Говорят, что функция y=f(x) имеет в точке c локальный max(min), если найдется такая окрестность точки с, в пределах которой значение f(с) является наибольшим (наименьшим) среди всех значений этих функций.

Док-во: По условию теоремы существует конечная производная f ‘(с). Так как функция y=f(x) имеет в точке с локальный экстремум, то она не может в этой точке с не возрастать, ни убывать. Значит в силу леммы о достаточном условии возрастания и убывания функции в точке ( Если функция y=f(x) дифференцируема в точке с и f ’(c) >0 ( f ‘(c) 2 / 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник