диск радиусом 10 см вращается вокруг неподвижной оси так что зависимость угла поворота радиуса диска
Диск радиусом 10 см вращается вокруг неподвижной оси так что зависимость угла поворота радиуса диска
вращается вокруг неподвижной оси
Сравните кинетическую энергию диска, вращающегося вокруг неподвижной оси и катящегося по горизонтальной плоскости. Линейная скорость точек на ободе диска одинакова.
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = At 2 (А = 0,5 рад/с 2 ). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное аτ, нормальное аn и полное а ускорения.
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = At 2 (А = 0,1 рад/с 2 ). Определите полное ускорение а точки на ободе диска к концу второй секунды после начала движения, если линейная скорость той точки в этот момент равна 0,4 м/с.
Сплошной шар диаметром 20 см и массой 35 кг вращается вокруг неподвижной оси, проходящей через его центр, с частотой 5 об/с. На шар подействовал постоянный вращающий момент, вследствие чего шар сделал 200 об за 15 с. Найти величину вращающего момента.
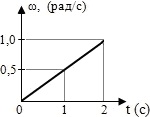
Маховик вращается вокруг неподвижной оси по закону, представленному на графике. Вращающий момент равен 10 Н·м. Определить момент инерции маховика.
1.1 Элементы кинематики
UptoLike
Диск радиусом R = 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = A + Bt3 (A = 2 рад; B = 4 рад/с3).
Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = At + Bt2 (A = 0,3 м/с2; B = 0,1 м/с3). Определите угол α, который образует вектор полного ускорения a с радиусом колеса через 2 с от начала движения.
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt2 (A = 0,1 рад/с2).
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt2 (A = 0,5 рад/с2).
Диск радиусом R = 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота диска от времени задается уравнением φ = A + Bt+ Сt2 + Dt3 (B = 1 рад/с, C = 1 рад/с2, D = 1 рад/с3).
Точка движется по окружности радиусом R = 15 см с постоянным тангенсальным ускорением aτ. К концу четвертого оборота после начала движения линейная скорость точки v1 = 15 см/с. Определить нормальное ускорение an2 точки через t2 = 16 c после начала движения.
Колесо автомобиля вращается равнозамедленно. За время t = 2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
Якорь электродвигателя, имеющий частоту вращения n = 50 с-1, после выключения тока, сделав N = 628 оборотов, остановился. Определить угловое ускорение ε якоря.
Колесо вращается с постоянным угловым ускорением ε = 3 рад/с. Определить радиус колеса, если через время t = 1 с после начала движения полное ускорение колеса равно а = 7,5 м/с2.
Линейная скорость v1 точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость v2 точки, находящейся на 6 см ближе к его оси. Определите радиус диска.