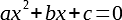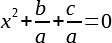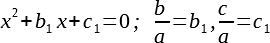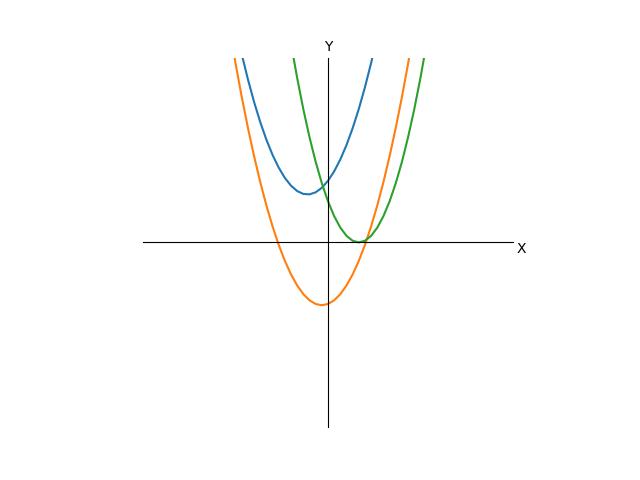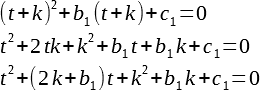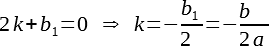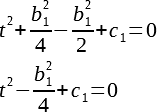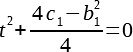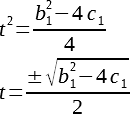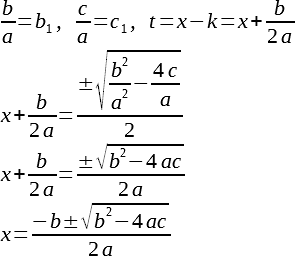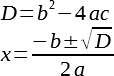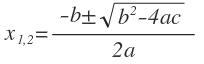дискриминант зачем нужен в жизни
Квадратные уравнения для гуманитариев и школьников.
Ну вот, наконец настало время запилить первый свой познавательный пост.
Все в школе решали квадратные уравнения, там вам рассказывали про дискриминант, что два корня, и все такое, причем, скорее всего, в подробности не вдаваясь. Мне в какой-то момент стало интересно, а почему все так, а не иначе, откуда взялись эти дискриминанты, почему корней два, а не три или сколько-то еще. Вообще, я люблю представлять себя математиком древности, который открывает что-нибудь. Типа, вот раньше чего-то не было, а он взял и вывел. Как это могло происходить?
Конечно, я буду использовать современные достижения математики, которые, возможно, не были известны первооткрывателям тех же квадратных уравнений, но строгости это не уменьшает, поэтому такой подход меня устраивает.
Итак, что же такое квадратное уравнение? Это уравнение вида:
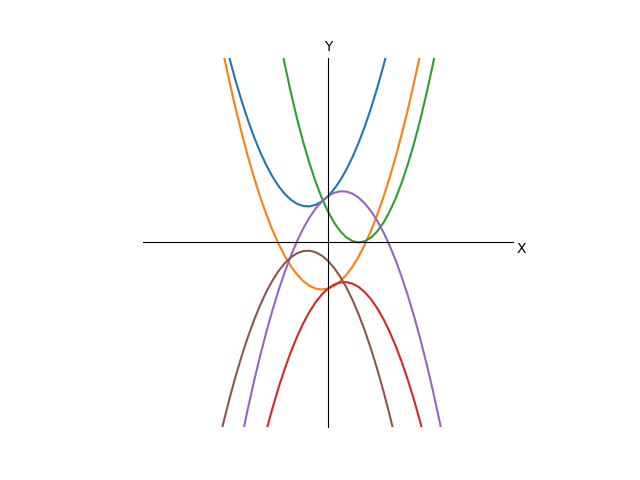
У нас тут общий случай, то-есть неизвестны конкретные значения констант, поэтому честно нарисовать график квадратичной функции сразу мы не можем. Сперва я хотел исследовать функцию всеми доступными методами(дабы аргументированно рисовать график), но потом решил, что, раз для нахождения решения нам нам хватит чисто арифметических действий, лучше не усложнять и не лезть в производные. Поэтому я решил нарисовать несколько графиков, неподходящие из которых мы будем отсеивать по мере продвижения к решению.
Итак, допустим, наша функция будет представлять собой один из графиков, пока мы не знаем, какой.
Теперь, попробуем как-нибудь изменить исходную функцию, чтобы она стала проще, но сохранила свойства исходной. У нас три константы, а это многовато, давайте попробуем избавиться от как можно большего их количества. Для начала, мы можем поделить все уравнение на a. а заведомо не равна нулю, так как если бы была равна, наше уравнение превратилось бы в простое линейное, которое, будем считать, уже всем известно, как решать. Тогда у нас получится новое уравнение:
Чтобы не тащить возможное нагромождение дробей, мы назовем для краткости константы новыми именами, а уравнение преобразуется к виду:
А что там с графиком стало от такого преобразования? По сути, на правую часть уравнения это никак не повлияло, а функция слева сжалась(или растянулась, в зависимости от того, больше модуль а, чем единица, или меньше) пропорционально коэффициенту a к осиX, а если а было отрицательным, то еще и перевернулась вверх ногами. Самое важное здесь для нас то, что пересечение графиков с осью X вообще никак не изменилось, значит, искомое решение уравнения осталось тем же самым. Кроме того, теперь мы можем быть точно уверены, что у новой функции «рога» направлены вверх, ведь х в квадрате теперь с положительным коэффициентом, а значит, при больших по модулю значениях х, как не трудно догадаться, этот член будет положительным и будет расти быстрее, чем оставшиеся два члена.
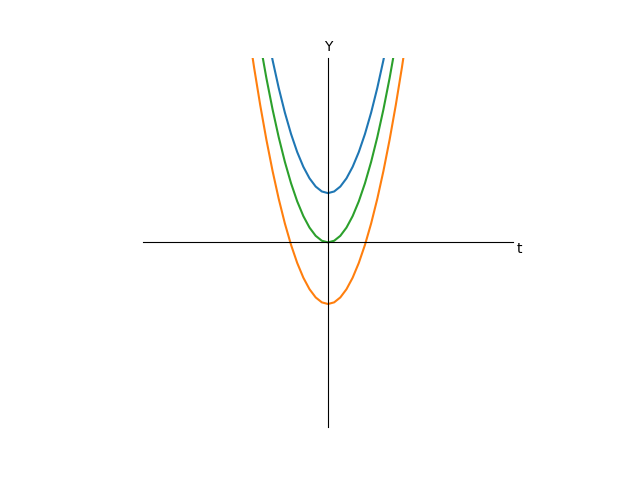
Теперь наши графики буду выглядеть как-то так, мы убрали из них все те, что рогами вниз:
Все внимание на коэффициент перед t в первой степени. Благодаря тому, что мы можем k выбрать произвольно, мы можем сделать так, чтобы этот коэффициент стал равным нулю, а значит, t в первой степени исчезнет из уравнения, и оно еще упростится!
Подставим найденное k в предыдущее выражение, упростим, получим:
Как видно, переменная t осталась только в виде квадрата без коэффициентов, все остальное ушло в одну константу. Но что вообще это преобразование делает с графиком? Оно просто-напросто сдвигает график влево на расстояние k(если k положительное, и в вправо в противном случае). Стало быть, если у нас было пересечение с нулем, то оно и останется, но сдвинется в какую-то сторону, а если не было, то его и не появится. Можно заметить, что если мы поменяем t на -t, то ничего не изменится(квадрат аннигилирует минус), значит, функция стала четной, отражение графика функции от оси Y ничего не меняет, следовательно, преобразование, которое мы сделали, превращает график в симметричный относительно оси Y, причем все линии одинаковые, за исключением того, что находятся на разной высоте.
Рассмотрим повнимательнее последнее выражение, его можно переписать в виде:
Очевидно, что так как t в квадрате может быть только неотрицательным, то минимум функции достигается при t=0. Следовательно, если второе слагаемое(а можно считать, что только его числитель) положительно, то функция до нуля не достанет и решений уравнения, стало быть, нет. Это случай синей кривой на графике. Если нам так повезло, что что слагаемое равно нулю, то очевидным единственным решением будет 0, это зеленая кривая. Если же слагаемое отрицательно, то существуют какие-то решения, это оранжевая кривая. Это три случая, имеют принципиальную разницу, все остальное многообразие возможных уравнений сводится к этим трем. Теперь разберемся, сколько же там корней. Выразим t из последнего выражения(будем считать, что обратную функцию для квадрата мы знаем):
Но мы нашли какое-то t, а нам ведь надо найти х. Для этого, выполним все преобразования, которые мы сделали над уравнением, теперь уже над его решением в обратном порядке, а именно просто подставим все то, что мы назаменяли:
Ой, а что это у нас тут под корнем такое знакомое. Да это же дискриминант!
Ну вот, собственно, и все, решение получено. Хотел еще про правила Виета написать, но, думаю не стоит, пост и так большой, а правила эти весьма просты.
Как найти дискриминант квадратного уравнения
Понятие квадратного уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.
Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Есть три вида квадратных уравнений:
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Чаще всего для поиска дискриминанта используют формулу:
В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:
Эта формула подходит даже для неполных квадратных уравнений.
Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.
Как решать квадратные уравнения через дискриминант
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!
Примеры решения квадратных уравнений с помощью дискриминанта
Ответ: корень уравнения 3.
Нахождение дискриминанта, формула, сравнение с нулём
Квадратный многочлен, как искать его корни
Как это значение показывает наличие вещественных корней:
Варианты расчётов для закрепления материала
Использование дискриминанта в вычислении корней
Эта вспомогательная конструкция не только показывает количество вещественных решений, но и помогает их находить. Общая формула расчёта для уравнения второй степени такова:
Результат приравнивания квадратного выражения к нулю вычисляется согласно алгоритму:
Некоторые частные случаи
В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство. Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:
Если свободный член нулевой, то корни будут
Но есть и другие частные случаи, упрощающие нахождение решения.
Приведенное уравнение второй степени
Важно отметить, что i * w ^ 2 + j * w + k = 0 удастся привести путём деления на «i». Результат будет: w ^ 2 + j1 * w + k1 = 0, где j1 равно j / i и k1 равно k / i.
Чётный второй множитель
Более высокий порядок дискриминанта
Рассмотрим i * w ^ 3 + j * w ^ 2 + k * w + m = 0.
Что такое дискриминант-1
Рисуем графики:
Теперь оставим с одинаковыми, а поиграем с b:
Обнаруживаем, что от b зависит местонахождение вершины параболы, причем координата Х вершины равна -b/2, а сама парабола вроде бы одна и та же, просто сдвигается относительно оси Y.
Теперь попробуем выяснить, на что влияет коэффициент а:
Сразу видно, что и ветки параболы сжимаются при увеличении а, и вершина параболы сдвигается, то есть, тоже зависит от а. Путем несложных подсчетов выясняем, что координата X вершины параболы вычисляется как -b/2a.
От знака коэффициента а зависит, куда смотрят ветки параболы:
При положительных а ветки смотрят вверх, при отрицательных а ветки смотрят вниз, при а=0 парабола превращается в прямую.
А что же дискриминант?
Если в последней картинке рассчитать дискриминанты, то выяснится, что, когда вся парабола выше оси Х, дискриминант будет отрицательным и корней у уравнения не будет, а точнее не будет точек пересечения параболы с осью Х (этого в школе не говорили вроде).
Если дискриминант положительный, то парабола пересекает ось Х в двух точках, и у нас есть два корня уравнения.
Если дискриминант равен нулю, только вершина параболы касается оси Х, и корень уравнения всего один.
Но интереснее случай, когда а=0, и тогда уравнение превращается в линейное, вернее, парабола превращается в линию. Интереснее потому, что формально дискриминант в этом случае можно рассчитать, и линия будет иметь точку пересечения с осью Х, но корень уравнения по школьной формуле вычислить нельзя, потому что в знаменателе дроби будет ноль.
Зачем нужен дискриминант?
Чтобы проще решить уравнение и проверить, есть ли действительные решения.
Если Q = 0, то уравнение имеет 1 действительный и 2 равных действительных корня (или 3 равных).
Могу посоветовать сайт, которым пользуемся мы, когда ищем ответы по математике. Он называется слово, потом точка, потом домен ws (а не ru).
Там постранично отсканирован решебник, просто и понятно изложено. Вот выдержка именно из него:
Там есть и другие решебники, пригодятся ребенку позже.
Есть еще математикус.ру.
Есть сайт алленг.ру, там можно помимо готовых домашних заданий найти учебники (в том числе и для высшего и средне-профессионального образования), их количество постоянно пополняется.
Можно поискать в книжных магазинах.
Если раньше все школы нашей необъятной Родины учились по единому учебнику, то в настоящее время учебников по одному и тому же предмету развелось вагон и маленькая тележка.
Математика на экономических специальностях не слишком сложная, в основном статистика.
Можно попробовать пересчитать. Хотя бы приблизительно.