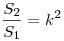если два угла одного треугольника равны двум углам другого то такие треугольники подобны верно

Если два угла одного треугольника равны двум углам другого то такие треугольники подобны верно

Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно по признаку подобия треугольников.

2) «Вертикальные углы равны» — верно, это теорема планиметрии.

3) «Любая биссектриса равнобедренного треугольника является его медианой» — неверно, это утверждение справедливо только для равностороннего треугольника.

Заметим, что признак подобия треугольников в учебнике геометрии сформулирован так: «если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны». В утверждении номер 1 опущено слово «соответственно», что не меняет сути.

Укажите номера верных утверждений.

1) Существует квадрат, который не является прямоугольником.

2) Если два угла треугольника равны, то равны и противолежащие им стороны.

3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Существует квадрат, который не является прямоугольником» — некорректное утверждение, корректное — «Существует прямоугольник, который не является квадратом».

2) «Если два угла треугольника равны, то равны и противолежащие им стороны» — верно, т. к. треугольник, два угла которого равны является равнобедренным, причём равные стороны лежат напротив равных углов.

3) «Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны» — верно, это теорема планиметрии.

Укажите номера верных утверждений.

1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части» — верно по свойству равнобедренного треугольника.

2) «В любом прямоугольнике диагонали взаимно перпендикулярны» — неверно, это утверждение справедливо только для прямоугольника, у которого все стороны равны, то есть для квадрата.

3) «Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу» — верно, т. к. окружность — множество точек, находящихся на заданном расстоянии от данной точки.

Источник

Если два угла одного треугольника равны двум углам другого то такие треугольники подобны верно

Какие из следующих утверждений верны?

1) Площадь треугольника меньше произведения двух его сторон.

2) Средняя линия трапеции равна сумме её оснований.

3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Проверим каждое из утверждений.

1) «Площадь треугольника меньше произведения двух его сторон» — верно, так как площадь треугольника равна где — угол между сторонами и треугольника. Синус угла всегда меньше единицы, поэтому площадь треугольника меньше произведения двух его сторон.

2) «Средняя линия трапеции равна сумме её оснований» — неверно, средняя линия трапеции равна полусумме его оснований.

3) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно, по признаку подобия треугольников.

Источник

Признаки равенства и подобия треугольников

Признаки равенства треугольников

Равными называют треугольники, у которых соответствующие стороны равны.

Теорема (первый признак равенства треугольников).
Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны.

Теорема (второй признак равенства треугольников).
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Теорема (третий признак равенства треугольников).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

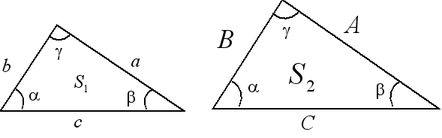
Признаки подобия треугольников

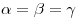
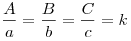
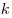
Подобными называются треугольники, у которых углы равны, а сходственные стороны пропорциональны: , , где — коэффициент подобия.

I признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.

II признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

III признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Следствие: Площади подобных треугольников относятся как квадрат коэффициента подобия: .

Источник