если смешанное произведение трех ненулевых векторов равно нулю то такие векторы являются
Вектор. Смешанное произведение векторов.
Также его называют тройным скалярным произведением векторов, скорее всего это связано с тем,
Смешанное произведение векторов — скалярное произведение вектора 
на векторное произведение векторов 
и 
.
Или другими словами:
Смешанным произведением векторов 
является число 
, состоящее из скалярного произведения вектора на векторное произведение векторов и . Смешанное произведение
векторов записывается следующим образом:
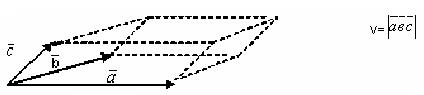
Геометрический смысл смешанного произведения векторов.
Геометрический смысл смешанного произведения векторов: если три вектора 
правые, то их
смешанное произведение равно объему параллелепипеда построенного на них:
.
В случае левой тройки , смешанное произведение указанных векторов равно объему
параллелепипеда со знаком “–“:
.
Если , и компланарны, то их смешанное произведение = 0.
Вывод: объем параллелепипеда, построенного на векторах , и равен модулю смешанного
произведения этих векторов:
Объем пирамиды, построенной на этой тройке этих векторов, находим по формуле:
Геометрические свойства смешанного произведения векторов.
1. Модуль смешанного произведения некомпланарных векторов равен объему 
параллелепипеда, построенного на этих векторах. Произведение 
будет со знаком плюс, если
тройка векторов — правая, и будем иметь отрицательный знак, если тройка — левая,
2. Смешанное произведение =0 тогда и только тогда, когда векторы компланарны:
векторы компланарны.
Алгебраические свойства смешанного произведения векторов.
1. При перемене мест двух множителей смешанное произведение меняет знак на противоположный:
При циклической (круговой) перестановке множителей смешанное произведение остается без изменений:
2. Смешанное произведение линейно по любому множителю.
Первое свойство следует из первого геометрического свойства и свойств ориентации троек векторов, так
как от перестановки двух множителей местами, модуль смешанного произведения остается прежним, а
изменяется только ориентация тройки. При циклической перестановке векторов ориентация тройки
остается без изменений.
Второе свойство следует из линейности скалярного произведения и первого свойства.
Формула вычисления смешанного произведения векторов.
Теорема (формула вычисления смешанного произведения векторов):
Если у векторов в правом ортонормированном базисе 
координаты
, 
,
соответственно, то смешанное произведение их вычисляется по следующей формуле:
Из определения следует:
что и требовалось доказать.
Еще некоторые свойства смешанного произведения векторов.
1. 
2. 
4. Тройка векторов будет правой только если 
. Ежели 
, то векторы, и
создают левую тройку векторов.
5. 
6. 
7. 
8. 
9. 
10. Тождество Якоби: 
Если векторы 
, 
и 
заданы своими координатами, то их
смешанное произведение можно найти по формуле, приведенной ниже:
2.11 Смешанное произведение
Определение. Смешанным произведением трех векторов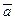 
, 
, 
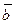
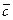
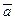
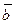
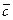
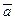
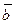
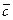
называется число, равное скалярному произведению вектора [´] на вектор , т. е. [´] × .
Свойства смешанного произведения
1.Смешанное произведение трех векторов равно нулю, если:
А) хоть один из перемножаемых векторов равен нулю;
Б) два из перемножаемых векторов коллинеарны;
В) все три вектора параллельны одной и той же плоскости (компланарны).
2. Смешанное произведение не изменится, если в нем поменять местами знаки векторного и скалярного умножения, т. е.
[´] ×· = × [´].
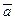
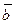
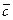
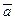
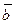
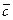
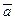
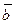
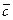
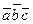
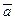
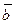
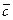
В силу этого свойства смешанное произведение векторов , и принято записывать так: 
. Можно показать, что Смешанное произведение трех векторов , , По модулю равно объему параллелепипеда, построенного на этих векторах. В этом состоит геометрический смысл смешанного произведения и определителя третьего порядка (рисунок 16).
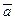
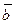
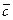
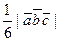
Объем V1 треугольной пирамиды, построенной на векторах , , , вычисляется по формуле V1 = 
.
Из свойств смешанного произведения вытекает следующее: необходимым и достаточным Условием компланарности трех векторов служит условие равенства нулю их смешанного произведения 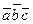= 0 (объем параллелепипеда равен нулю).
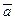
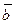
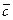
Пусть векторы заданы своими координатами =<A1, A2, A3>, = <B1, B2, B3>, = <C1, C2, C3>.
Тогда их Смешанное произведение можно Вычислить по формуле
(2.29)
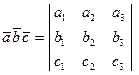
Таким образом, если три вектора лежат в одной плоскости, то
(2.30)
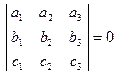
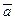
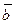
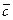
Итак, в случае компланарности векторов один из векторов линейно выражается через другие, то есть векторы , , линейно зависимы.
Отсюда следует свойство определителя: если строки (столбцы) определителя линейно зависимы, то определитель равен нулю.
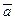
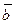
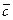
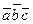
Если векторы , , образуют правую тройку, то их смешанное произведение положительно: > 0 означает, что эти векторы образуют правую тройку.
Вектор. Смешанное произведение векторов.
Также его называют тройным скалярным произведением векторов, скорее всего это связано с тем,
Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и .
Или другими словами:
Смешанным произведением векторов является число , состоящее из скалярного произведения вектора на векторное произведение векторов и . Смешанное произведение
векторов записывается следующим образом:
Геометрический смысл смешанного произведения векторов.
Геометрический смысл смешанного произведения векторов: если три вектора правые, то их
смешанное произведение равно объему параллелепипеда построенного на них:
.
В случае левой тройки , смешанное произведение указанных векторов равно объему
параллелепипеда со знаком “–“:
.
Если , и компланарны, то их смешанное произведение = 0.
Вывод: объем параллелепипеда, построенного на векторах , и равен модулю смешанного
произведения этих векторов:
Объем пирамиды, построенной на этой тройке этих векторов, находим по формуле:
Геометрические свойства смешанного произведения векторов.
1. Модуль смешанного произведения некомпланарных векторов равен объему
параллелепипеда, построенного на этих векторах. Произведение будет со знаком плюс, если
тройка векторов — правая, и будем иметь отрицательный знак, если тройка — левая,
2. Смешанное произведение =0 тогда и только тогда, когда векторы компланарны:
векторы компланарны.
Алгебраические свойства смешанного произведения векторов.
1. При перемене мест двух множителей смешанное произведение меняет знак на противоположный:
При циклической (круговой) перестановке множителей смешанное произведение остается без изменений:
2. Смешанное произведение линейно по любому множителю.
Первое свойство следует из первого геометрического свойства и свойств ориентации троек векторов, так
как от перестановки двух множителей местами, модуль смешанного произведения остается прежним, а
изменяется только ориентация тройки. При циклической перестановке векторов ориентация тройки
остается без изменений.
Второе свойство следует из линейности скалярного произведения и первого свойства.
Формула вычисления смешанного произведения векторов.
Теорема (формула вычисления смешанного произведения векторов):
Если у векторов в правом ортонормированном базисе координаты, ,
соответственно, то смешанное произведение их вычисляется по следующей формуле:
Из определения следует:
что и требовалось доказать.
Еще некоторые свойства смешанного произведения векторов.
1.
2.
4. Тройка векторов будет правой только если . Ежели , то векторы, и
создают левую тройку векторов.
5.
6.
7.
8.
9.
10. Тождество Якоби:
Если векторы , и заданы своими координатами, то их
смешанное произведение можно найти по формуле, приведенной ниже: