если стороны одного угла соответственно параллельны сторонам другого угла то такие углы или равны
Если стороны одного угла соответственно параллельны сторонам другого угла то такие углы или равны
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке докажем две теоремы об углах с соответственно параллельными или перпендикулярными сторонами и рассмотрим задачу на их применение.
Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.
Дано: неразвернутые углы АОВ и МNК, и ОА||NМ, ОВ||NК.
Доказать: либо углы АОВ и МNК равны, либо сумма углов АОВ и МNК равна 180º.
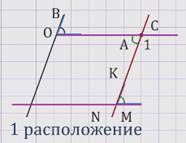
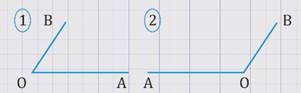
Рассмотрим случаи расположения углов АОВ и МNК (см. рисунок).
Доказательство для первого расположения углов.
Прямая NК пересекает прямую ОА в некоторой точке С.
Параллельные прямые ОВ и NК пересечены секущей ОС, поэтому угол 1 равен углу АОВ – как накрест лежащие углы при параллельных прямых ОВ и NК и секущей ОС.
Параллельные прямые ОА и NМ пересечены секущей NС, поэтому угол 1 равен углу МNК – как накрест лежащие углы при параллельных прямых ОА и NМ и секущей NС.
Из двух равенств получаем, что ∠АОВ = ∠МNК.
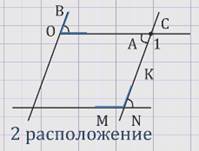
При втором расположении углов:
параллельные прямые ОВ и NК пересечены секущей ОС, поэтому угол 1 равен углу АОВ – как накрест лежащие углы при параллельных прямых ОВ и NК и секущей ОС.
Параллельные прямые ОА и NМ пересечены секущей NС, поэтому сумма угла 1 и угла МNК = 180º, как сумма односторонних углов при параллельных прямых ОА и NМ и секущей NС.
Из двух равенств получаем, что ∠ АОВ + ∠МNК = 180º.
Рассмотрим следующее утверждение.
Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.
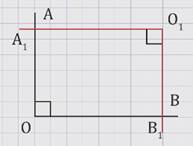
неразвернутые углы АОВ и A1O1B1, луч ОА перпендикулярен лучу O1A1, луч ОВ перпендикулярен лучу O1B1.
либо углы АОВ и A1O1B1 равны, либо сумма углов АОВ и A1O1B1 равна 180º.
здесь необходимо рассмотреть несколько случаев.
Если угол АОВ прямой, то и угол A1O1B1 тоже прямой, поэтому эти углы равны и в сумме составляют 180º.
Остаются варианты, когда угол АОВ меньше 90º и когда угол АОВ больше 90º.
Рассмотрим подробнее первый случай.
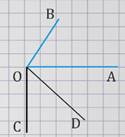
Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными, а точки В и С лежали по разные стороны от прямой ОА.
Теперь проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными, а точки С и D лежали по одну сторону от прямой ОА.
Так как угол АОВ равен 90º минус угол АОD и угол СОD равен 90º минус угол АОD по построению, то из двух этих равенств следует, что угол АОВ равен углу СОD.
Используя утверждение о том, что две прямые, перпендикулярные одной и той же прямой, параллельны, можно прийти к выводу, что стороны угла СОD соответственно параллельны сторонам угла A1O1B1, поэтому либо ∠СОD = ∠A1O1B1, либо сумма углов ∠СОD и ∠ A1O1B1= 180º.
Следовательно, либо ∠АОВ = ∠A1O1B1, либо сумма углов ∠АОВ и ∠A1O1B1= 180º.
Второй случай, когда угол АОВ больше 90º, докажите самостоятельно.
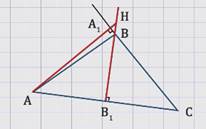
Прямые, содержащие высоты АA1 и ВB1 треугольника АВС, пересекаются в точке Н, угол В – тупой, угол С = 20º.
Так как треугольник тупоугольный, угол В тупой, то высоты АA1 и ВB1 треугольника АВС пересекутся в точке Н за пределами треугольника (см. рисунок).
Рассмотрим углы АНB1 и АСA1.
Стороны угла АНB1 соответственно перпендикулярны сторонам угла АСA1, а по ранее доказанной теореме такие углы равны.
Значит, угол АНВ = 20º.
Итак, в этом уроке мы доказали две теоремы об углах с соответственно параллельными или перпендикулярными сторонами и решили задачу по теме урока.
Углы с соответственно параллельными или перпендикулярными сторонами
Докажем теорему об углах с соответственно параллельными сторонами.
| Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180°. |
Пусть ∠AOB и ∠A1O1B1 — данные углы и ОА || О1А1, ОВ || О1В1. Если угол АОВ развёрнутый, то и угол А1О1В1 — развёрнутый (объясните почему), поэтому эти углы равны. Пусть ∠AOB — неразвёрнутый угол. Возможные случаи расположения углов АОВ и А1О1В1 изображены на рисунке 115, а и б. Прямая О1В1 пересекает прямую О1А1 и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М. Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов, образованных при пересечении прямых О1В1 и ОА (угол 1 на рисунке 115), равен углу АОВ (как накрест лежащие углы). Параллельные прямые ОА и О1А1 пересечены секущей О1М, поэтому либо ∠1 = ∠A1O1B1 (рис. 115, а), либо ∠1 + ∠A1O1B1 = 180° (рис. 115, б). Из равенства ∠1 = ∠AOB и последних двух равенств следует, что либо ∠AOB = ∠A1O1B1 (см. рис. 115, а), либо ∠AOB + ∠A1O1B1 = 180° (см. рис. 115, б). Теорема доказана.
Докажем теперь теорему об углах с соответственно перпендикулярными сторонами.
| Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие утлы или равны, или в сумме составляют 180°. |
Видеоурок «Углы с соответственно параллельными или перпендикулярными сторонами»
§ 1 Теорема об углах с соответственно параллельными сторонами
В этом уроке докажем две теоремы об углах с соответственно параллельными или перпендикулярными сторонами и рассмотрим задачу на их применение.
Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.
Дано: неразвернутые углы АОВ и МNК, и ОА||NМ, ОВ||NК.
Доказать: либо углы АОВ и МNК равны, либо сумма углов АОВ и МNК равна 180º.
Рассмотрим случаи расположения углов АОВ и МNК (см. рисунок).
Доказательство для первого расположения углов.
Прямая NК пересекает прямую ОА в некоторой точке С.
Параллельные прямые ОВ и NК пересечены секущей ОС, поэтому угол 1 равен углу АОВ – как накрест лежащие углы при параллельных прямых ОВ и NК и секущей ОС.
Параллельные прямые ОА и NМ пересечены секущей NС, поэтому угол 1 равен углу МNК – как накрест лежащие углы при параллельных прямых ОА и NМ и секущей NС.
Из двух равенств получаем, что ∠АОВ = ∠МNК.
При втором расположении углов:
параллельные прямые ОВ и NК пересечены секущей ОС, поэтому угол 1 равен углу АОВ – как накрест лежащие углы при параллельных прямых ОВ и NК и секущей ОС.
Параллельные прямые ОА и NМ пересечены секущей NС, поэтому сумма угла 1 и угла МNК = 180º, как сумма односторонних углов при параллельных прямых ОА и NМ и секущей NС.
Из двух равенств получаем, что ∠ АОВ + ∠МNК = 180º.
§ 2 Теорема об углах с соответственно перпендикулярными сторонами
Рассмотрим следующее утверждение.
Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.
неразвернутые углы АОВ и A1O1B1, луч ОА перпендикулярен лучу O1A1, луч ОВ перпендикулярен лучу O1B1.
либо углы АОВ и A1O1B1 равны, либо сумма углов АОВ и A1O1B1 равна 180º.
здесь необходимо рассмотреть несколько случаев.
Если угол АОВ прямой, то и угол A1O1B1 тоже прямой, поэтому эти углы равны и в сумме составляют 180º.
Остаются варианты, когда угол АОВ меньше 90º и когда угол АОВ больше 90º.
Рассмотрим подробнее первый случай.
Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными, а точки В и С лежали по разные стороны от прямой ОА.
Теперь проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными, а точки С и D лежали по одну сторону от прямой ОА.
Так как угол АОВ равен 90º минус угол АОD и угол СОD равен 90º минус угол АОD по построению, то из двух этих равенств следует, что угол АОВ равен углу СОD.
Используя утверждение о том, что две прямые, перпендикулярные одной и той же прямой, параллельны, можно прийти к выводу, что стороны угла СОD соответственно параллельны сторонам угла A1O1B1, поэтому либо ∠СОD = ∠A1O1B1, либо сумма углов ∠СОD и ∠ A1O1B1= 180º.
Следовательно, либо ∠АОВ = ∠A1O1B1, либо сумма углов ∠АОВ и ∠A1O1B1= 180º.
Второй случай, когда угол АОВ больше 90º, докажите самостоятельно.
§ 3 Задача на применение теорем об углах с соответственно параллельными или перпендикулярными сторонами
Прямые, содержащие высоты АA1 и ВB1 треугольника АВС, пересекаются в точке Н, угол В – тупой, угол С = 20º.
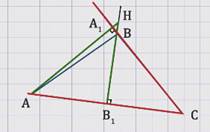
Так как треугольник тупоугольный, угол В тупой, то высоты АA1 и ВB1 треугольника АВС пересекутся в точке Н за пределами треугольника (см. рисунок).
Рассмотрим углы АНB1 и АСA1.
Стороны угла АНB1 соответственно перпендикулярны сторонам угла АСA1, а по ранее доказанной теореме такие углы равны.
Значит, угол АНВ = 20º.
Итак, в этом уроке мы доказали две теоремы об углах с соответственно параллельными или перпендикулярными сторонами и решили задачу по теме урока.
Презентация, геометрия 7 класс по теме: Углы с соответственно параллельными или перпендикулярными сторонами
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Описание слайда:
Углы с соответственно параллельными или перпендикулярными сторонами
Описание слайда:
Теорема:
если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180 градусов
Описание слайда:
Дано: АОВ, А1О1В1, ОАО1А1, ОВО1В1.
Доказать: АОВ = А1О1В1 или АОВ + А1О1В1 = 1800.
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Прямая О1В1 пересекает прямую О1А1 и, следовательно, пересекает параллельную еПй прямую ОА в некоторой точке М (смотри следствие 10 из аксиомы параллельных прямых). Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов (1), образованных при пересечении прямых О1В1 и ОА (Рис.2) равен углу АОВ, т.е. 1 = АОВ (по теореме о накрест лежащих углах). Параллельные прямые ОА и О1А1 пересечены секущей О1М, поэтому 1 = А1О1В1.
Из равенств 1 = АОВ и 1 = А1О1В1 следует, что АОВ =А1О1В1.
Описание слайда:
Описание слайда:
Прямая О1В1 пересекает прямую О1А1 и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М (смотри следствие 10 из аксиомы параллельных прямых). Параллельные прямые ОВ и О1В1 пересечены секущей ОМ, поэтому один из углов (1), образованных при пересечении прямых О1В1 и ОА (Рис.3) равен углу АОВ, т.е. 1 +А1О1В1 = 1800 (по теореме об односторонних углах). Параллельные прямые ОА и О1А1 пересечены секущей О1М, поэтому 1 = А1О1В1.
Из равенств 1 = АОВ и 1 +А1О1В1 = 1800 следует, что АОВ +А1О1В1 = 1800. Что и требовалось доказать.
Второй случай (рис.3)
Описание слайда:
Теорема:
если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы равны, или в сумме составляют 180 градусов.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Международная дистанционная олимпиада Осень 2021
Похожие материалы
Презентация к внеклассному мероприятию «Мир в цифрах»
Материалы для учителя в помощь подготовки к ОГЭ-решение задач по геометрии повышенной сложности
Презентация к внеклассному мероприятию «Математическая шкатулка»
Материалы для учителя в помощь подготовки к ОГЭ-решение задач по геометрии повышенной сложности
Презентация по геометрии 8 класс «Ромб»
Зачет № 2 по геометрии «Признаки параллельности прямых»
Контрольная работа по теме :»Тела вращения»
Презентация к уроку геометрии для 7 класса на тему «Признаки параллельных прямых»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5302926 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Москве запустили онлайн-проект по борьбе со школьным буллингом
Время чтения: 2 минуты
В России выбрали топ-10 вузов по работе со СМИ и контентом
Время чтения: 3 минуты
Путин попросил привлекать родителей к капремонту школ на всех этапах
Время чтения: 1 минута
В Тюменской области продлили на неделю дистанционный режим для школьников
Время чтения: 1 минута
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
Шойгу предложил включить географию в число вступительных экзаменов в вузы
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Признаки равенства треугольников
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.