если значение функции максимально в некоторой окрестности данной точки то такой максимум называется

Максимум и минимум функции

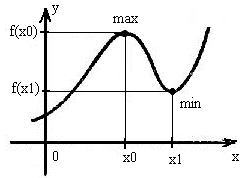
Определение.Точка х₀ называется точкой максимума(точкой минимума) функции , если существует такая δ-окрестность точки х₀, что для всех из этой окрестности выполняется неравенство .

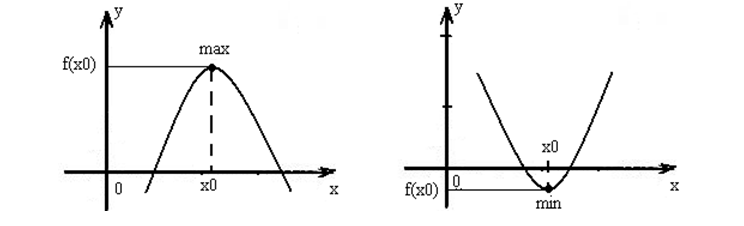
Рисунок 1. – Точка максимума.	Рисунок 2. – Точка минимума.

Определение.Значение функции в точке максимума (точке минимума) называется максимумом (минимумом) функции.

Определение. Максимум и минимум функции называются экстремумами функции.

Теорема(необходимое условие экстремума – НУЭ).

Если дифференцируемая функция имеет экстремум в точке х₀, то ее производная в этой точке равна нулю: .

Геометрически равенство означает, что в точке экстремума дифференцируемой функции касательная к ее графику параллельна оси Ох.

Обратная теорема неверна, т. е. если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Например, производная функция 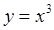точке равна нулю, однако в этой точке функция имеет только перегиб, а не экстремум.

Замечание. Непрерывная функция может иметь экстремум только в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.

Теорема(достаточное условие экстремума – ДУЭ-1).

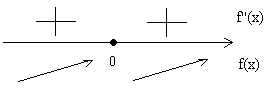
Если непрерывная функция у=f(x) дифференцируема в некоторой окрестности критической точки х₀ (за исключением, быть может, самой точки х₀) и при переходе через нее слева направо производная f ¢ (x) меняет знак с «+» на «–», то х₀ есть точка максимума, а с «–» на «+», то х₀ – точка минимума.

Исследовать функцию на экстремум означает найти все ее экстремумы. Из теорем НУЭ и ДУЭ-1 вытекает следующая схема исследования функции на экстремумы:

1) найти область определения функции;

2) найти производную функции;

3) найти критические точки функции;

4) выбрать из них только те, которые являются внутренними точками области определения функции;

5) исследовать знак производной 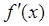слева и справа от каждой из выбранных критических точек;

6) в соответствии с теоремой ДУЭ-1 выписать точки экстремума (если есть);

7) вычислить значение функции в найденных точках экстремума.

Пример.Найти экстремумы функции .

Решение: исследуем функцию по приведенной выше схеме.

1) .

2) .

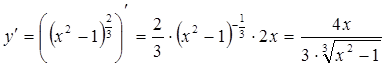
3) Решим уравнение , т.е. . Получим , .

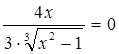
4) Точки, подозрительные на экстремум: , , , т.к. исходная функция определена в точках .

5) Исследуем знак производной:

6) – точки минимума, – точка максимума;

7) , .

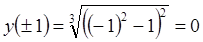
Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.

Теорема (достаточное условие экстремума – ДУЭ-2).

Если в точке первая производная функции равна нулю , а вторая производная в точке существует и отлична от нуля , то при в точке функция имеет максимум и минимум – при .

Источник

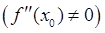
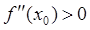
Если значение функции максимально в некоторой окрестности данной точки то такой максимум называется

СГА | АУП | Витте | Курсовые | Тесты | Помощь запись закреплена

Предмет: Методы оптимальных решений 4922.02.01;МТ.02;1

1. Внешнее воздействие на процесс, изменяющее его ход в желаемом направлении, называется воздействием.

2. Допустимое решение, при котором целевая функция минимальна (или максимальна), называется решением.

3. Другое название метода половинного деления – метод

4. Если в задаче поиска экстремума функции на функцию накладывается дополнительные условия, то такая задача называется задачей на экстремум.

5. Если значение функции максимально в некоторой окрестности данной точки, то такой максимум называется

7. Значение функции, максимальное на всей области определения, называется максимумом.

8. Значение функции, минимальное на всей области определения, называется максимумом.

9. Задачи теории принятия решения, в которых входные управляющие параметры не влияют на целевую функцию, называются

10. Концепция, основным положением которой является то, что все люди знают альтернативы, имеющиеся в данной ситуации, и все последствг: которые они вызовут называется концепцией___________

11. Критерий сравнения альтернатив в задачах принятия решения называется (ответ дать словосочетанием).

12. Метод золотого сечения относится к методам оптимизации.

13. Математическая зависимость, позволяющая без экспериментов, зная управляющие воздействия, определить выходные параметры, называет (ответ дать словосочетанием).

14. Методы нелинейного программирования в зависимости от способа задания шага итераций подразделяются на (ответ дайте числом) основных класса

15. Оператор, отражающий зависимость выходных параметров у от входных управляющих параметров, называется

16. Объективное единство закономерно связанных друг с другом предметов и явлений в природе и обществе называется

17. Основной задачей теории принятия решения является нахождение решения.

18. Основным методом решения задач линейного программирования является метод.

19. Область допустимых решений в задаче линейного программирования, содержащей две переменные, в общем случае имеет вид

21. Параметры системы, которые молено изменить в соответствии с нашим желанием, называются (ответ дать словосочетанием).

22. Решение, удовлетворяющее всем ограничениям задачи, называется решением.

23. Решение в задаче линейного программирования в общем случае достигается на области допустимых значений.

24. Согласно методу Лагранжа для решения задач на условный экстремум функции вводятся дополнительные неопределенные множители

25. Совокупность математических дисциплин, относящихся к организационному управлению, составляют теорию принятия решений или исследования______________.

26. С помощью метода прямого сканирования находится экстремум.

27. Условие, состоящее в том, что все главные миноры матрицы коэффициентов являются положительными, называется условием

28. Укажите соответствие:
Хорошо структурированные или количественно сформулированные проблемы в теории принятия решений
Слабо структурированные проблемы
Неструктурированные или качественно выраженные проблемы
Смешанные проблемы

проблемы, в которых количественные зависимости между признаками и характеристиками совершенно неизвестны
проблемы, содержащие как количественные, так и качественные элементы приблизительно в равных пропорциях
задачи теории принятия решений, в которых качественные оценки преобладают
задачи в теории принятия решений, в которых можно получить численные оценки

29. Укажите соответствие:
Задачи, в которых целевая функция и ограничения выражаются линейными функциями, решаются с помощью методов
Классы поисковых задач решаются с помощью методов
Состязательные задачи решаются методами
Задачи календарного планирования решаются с помощью методов

теории игр
теории расписаний
линейного программирования
нелинейного программирования

30. Укажите соответствие:
2-м этапом в процессе выработки решения является
3-м этапом в процессе выработки решения является
4-м этапом в процессе выработки решения является
1-м этапом в процессе выработки решения является

сбор данных об исследуемой системе
построение математической модели управляемой системы
формирование множества решений и оценка результатов
определение целей и критериев эффективности

31. Укажите соответствие:
Подход к принятию решений с точки зрения социальной системы
Подход к принятию решений с точки зрения поведения человека
Эмпирический подход при принятии решений
Подход с точки зрения принятия решения

подход, ориентирующийся на системы, в которых молено описать и рассчитать каждый фактор, которым молено управлять
подход, концентрируемый на человеческом аспекте управления или на здравом смысле
подход, согласно которому решения могут существовать независимо от конкретных ситуаций
подход, учитывающий не только индивидуальные аспекты, но и динамику работы группы, рассматривая при этом

32. Укажите соответствие:
Метод прямого сканирования
Экстремум функции многих переменных
Условный экстремум
Экстремум функции одной переменной

неопределенные множители Лагранжа
интервал неопределенности
критерий Сильвестра
равенство нулю первой производной

33. Укажите соответствие:
Необходимым и достаточным условием отрицательной определенности квадратичной формы для функции двух переменных является
Необходимое условие экстремума функции двух переменных
Необходимым и достаточным условием положительной определенности квадратичной формы для функции двух переменных является
При выполнении необходимого условия экстремума функции двух переменных, достаточным условием минимума функции

положительность четных главных миноров и отрицательность нечетных главных миноров коэффициентов квадратичной формы
положительность главных миноров матрицы коэффициентов квадратичной формы
равенство нулю ее частных производных
положительная определенность квадратичной формы

34. Укажите соответствие:
3-й этап в процессе принятия решений
2-й этап в процессе принятия решений
4-й этап в процессе принятия решений
1-й этап в процессе принятия решений

определение цели принятия решения
выбор из множества возможных решений наиболее эффективного
определение всех возможных способов или путей достижения цели
осознание того состояния или ситуации, в которой находится принимающий решение человек

35. Целевая функция в задаче линейного программирования, содержащей две переменные, имеет вид линии.

Источник

Если значение функции максимально в некоторой окрестности данной точки то такой максимум называется

§5. Экстремум функции. Монотонные функции. Наибольшее и наименьшее значение функции на отрезке

Точки локального максимума и локального минимума называют точками локального экстремума.

Если точка `a` является точкой локального экстремума функции `y=f(x)` и функция `f` имеет производную в этой точке, то `f^'(a)=0`.

Физический смысл: при одномерном движении с возвращением в точке максимального удаления должна быть остановка. Геометрический смысл: касательная в точке локального экстремума горизонтальна.

Из теоремы Ферма следует, что если функция имеет экстремум в точке `a`, то в этой точке производная функции либо равна нулю, либо не существует. Например, функция `y=|x|` имеет минимум в точке `x=0`, а производная в этой точке не существует (см. пример 4.2). Точки, в которых функция определена, а производная равна нулю или не существует, будем называть критическими.

Итак, если у функции имеются точки экстремума, то они лежат среди критических точек (критические точки «подозрительны» на экстремум). Для формулировки условий, обеспечивающих наличие экстремума в критической точке, нам потребуется следующее понятие.

Напомним, что под промежутком понимается интервал (конечный или бесконечный), полуинтервал или отрезок числовой прямой.

Пусть функция `y=f(x)` определена на промежутке `I`.

1) Функция `y=f(x)` возрастает на `I`, если для любых `x,yinI`, `x f(y)`.

Если функция возрастает или убывает на `I`, то говорят, что функция монотонна на промежутке `I`.

Условия монотонности. Пусть функция `y=f(x)` определена на промежутке `I` с концами `a`, `b`, дифференцируема на `(a, b)` и непрерывна в концах, если они принадлежат `I`. Тогда

1) если `f^'(x)>0` на `(a, b)`, то функция возрастает на `I`;

Исследовать функцию `y=x^3-3x` на монотонность и экстремумы на области определения.

Рассмотрим важный класс задач, в которых используется понятие производной – задачи нахождения наибольшего и наименьшего значения функции на отрезке.

Найти наибольшее и наименьшее значение функции `y=x^3-3x` на отрезке: а) `[-2;0]`; б) `[1;3]`.

б) Так как на луче `[1,+oo)` функция возрастает, то `y(1)

Отметим, что непрерывная на отрезке функция всегда имеет наибольшее и наименьшее значение.

Найти наибольшее и наименьшее значение функции `y=x^3-12|x+1|` на отрезке `[-4;3]`.

Отметим, что функция непрерывна на всей числовой прямой. Обозначим `f_1(x)=x^3+12(x+1)`, `f_2(x)=x^3-12(x+1)`. Тогда `y=f_1(x)` при `-4 0` на `(-4;-1)`, `y^'(x)=f_2^'(x) 0` на `(2;3)`. Запишем все исследования в таблице:

Источник

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.

\(- 9\): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является \(-2\).

Источник

Максимум и минимум функции

Вы будете перенаправлены на Автор24

Одним из этапов исследования функции является нахождение экстремумов заданной функции, другими словами, максимума и минимума функции.

Точки экстремума показаны на рис.

Экстремум параболы, рассматриваемой на всей области определения, совпадает с ее вершиной (рис.).

Значения заданной функции в точках минимума и максимума называются соответственно минимумом и максимумом заданной функции.

Экстремумы функции делятся на:

Определения 1 и 2 относятся к локальным экстремумам: локальный минимум и локальный максимум.

Наименьшее и наибольшее значения заданной функции на некотором промежутке являются глобальными экстремумами.

Глобальные экстремумы могут достигаться либо в точках локального экстремума, либо на концах отрезка.

Необходимое условие экстремума определяется следующей теоремой.

Готовые работы на аналогичную тему

Достаточные условия экстремума определяются следующими теоремами.

Алгоритм исследования заданной функции на экстремум включает следующие этапы:

Найдем критические и стационарные точки:

График заданной функции приведен на рис.

Найдем критические и стационарные точки:

$y(-3)=2\cdot (-3)^ <2>+12\cdot (-3)=2\cdot 9-36=18-36=-18$

Источник