евклидово пространство простыми словами что такое

Что такое Евклидово пространство?

Если заглянуть в справочники или энциклопедии, то можно найти следующий ответ на сформулированный выше вопрос: «Евклидово пространство – в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии» [1].

Действительно, в АКСИОМЕ 9 Евклид упоминает вскользь слово «пространство» [2]: «И две прямые не содержат пространства».

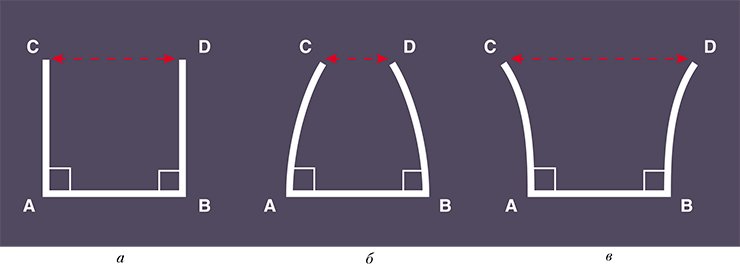
Фактически же, здесь, как и в во всех прочих аксиомах, речь идёт не о пространстве, а о плоскости, которая является лишь слоем пространства, толщиной в одну точку. Туманную формулировку 9-й аксиомы можно интерпретировать следующим образом [3]: «два отрезка не могут сходиться в двух различных точках – то есть ограничивать некоторую фигуру конечной площади» (см. рисунок слева).

Примечательно, что это единственное (!) упоминание слова «пространство» Евклидом. Больше мы не встретим даже намёка на пространство ни среди других аксиом, ни среди постулатов, ни среди определений его 15-томного труда.

Таким образом, согласно энциклопедиям, ЕВКЛИДОВО ПРОСТРАНСТВО (в изначальном смысле) – это плоскость, которую не содержат две прямые. 🙂

P.S. Из правого рисунка видно, что так называемые «пространства» Евклида, Лобачевского или Римана на самом деле являются лишь поверхностями с разными геометрическими свойствами.

1. Евклидово пространство: Материал из Википедии. – https://ru.wikipedia.org/wiki/Евклидово_пространство

2. Начала Евклида. Книги I-XV. Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при участии М. Я. Выгодского и И. Н. Веселовского. – Гос. изд-во технико-теоретич. лит-ры, М.-Л.: 1950. – 1299 с.

Источник

Евклидово пространство

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно -мерное евклидово пространство обозначается , хотя часто используется не вполне приемлемое обозначение .

1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

,

в простейшем случае (евклидова норма):

где (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:

,

где и .

Содержание

Связанные определения

Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

Более абстрактный пример:

Вариации и обобщения

См. также

Ссылки

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называется n мерное векторное пространство, в котором определено скалярное произведение … Большой Энциклопедический словарь

Евклидово пространство — пространство, свойства которого описываются аксиомами евклидовой геометрии. Упрощенно можно определить евклидово пространство, как пространство на плоскости или в трехмерном объеме, в которых заданы прямоугольные (декартовы) координаты, а… … Начала современного естествознания

Евклидово пространство — [Eu­c­lidean space] см. Многомерное (n мерное) векторное пространство, Векторное (линейное) пространство … Экономико-математический словарь

евклидово пространство — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN Cartesian space … Справочник технического переводчика

евклидово пространство — пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называют n мерное векторное пространство, в котором определено скалярное произведение. * * * ЕВКЛИДОВО ПРОСТРАНСТВО ЕВКЛИДОВО… … Энциклопедический словарь

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства к рого изучаются в евклидовой геометрии. В более широком понимании Е. п. наз. n мерное векторное пространство, в к ром определено скалярное произведение … Естествознание. Энциклопедический словарь

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства к рого описываются аксиомами евклидовой геометрии. В более общем смысле Е. п. конечномерное действительное векторное пространствоRn со скалярным произведением( х, у), х, к рое в надлежащим образом выбранных координатах… … Математическая энциклопедия

Евклидово пространство — (в математике) пространство, свойства которого описываются аксиомами евклидовой геометрии (См. Евклидова геометрия). В более общем смысле Е. п. называется n мepное Векторное пространство, в котором возможно ввести некоторые специальные… … Большая советская энциклопедия

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Евклидово пространство

Одной из важнейших задач геометрии является задача измерения расстояния между двумя объектами. В произвольном линейном пространстве мы пока не можем определить насколько «близки» между собой объекты. В настоящем разделе понятие расстояния между двумя векторами — элементами линейного пространства — будет вводиться посредством скалярного произведения векторов. Насколько обоснован такой порядок введения понятий:

Определения

Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:

Свойства

Теорема. Имеет место неравенство Коши–Буняковского:

С помощью скалярного произведения, введенного в предыдущем пункте, можно доказать справедливость интегральной формы неравенства:

Теорема. Имеет место неравенство треугольника

Пример. Найти расстояние между полиномами

Теперь прокомментируем последний пример. В разделе, посвященном полиному одной переменной, имеется теорема о непрерывной зависимости корней полинома от его коэффициентов. Смысл этого результата в следующем: если коэффициенты полиномов

Подводя итог приведенным рассуждениям, можно только повторить: метод, выбираемый для оценки близости между объектами, может зависеть от поставленной задачи. Микроскоп не пригоден для наблюдения за большими объектами, а телескоп — за малыми.

Следующий результат также имеет название, взятое из планиметрии, где он формулируется так: сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.

Теорема. В евклидовом пространстве имеет место равенство параллелограмма

Ортогонализация

Чему равно расстояние между двумя векторами ортонормированного базиса?

Пример. Ортогонализовать систему векторов

Пример. Пусть в пространстве полиномов скалярное произведение задается формулой

Следующая теорема устанавливает связь между двумя ортонормированными базисами в одном и том же пространстве.

Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.

Матричный формализм алгоритма Грама-Шмидта: QR-разложение

Пример. Для матрицы из предыдущего примера имеем:

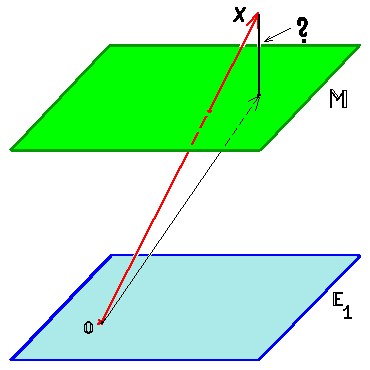
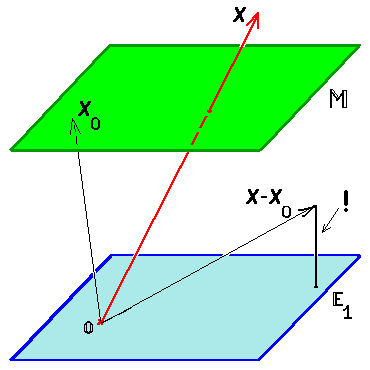
Расстояние от точки до многообразия

Пример. Множество

Доказать, что в пространстве квадратных матриц со скалярным произведением, заданным формулой

Вычисление расстояния

Альтернативный способ вычисления расстояния от точки до линейного многообразия, заданного системой линейных уравнений ☞ ЗДЕСЬ.

Доказательство ☞ ЗДЕСЬ.

Подводя итог: определители Грама полностью решают задачу о вычислении расстояния от точки до линейного подпространства в любом евклидовом пространстве; этот результат легко обобщается на произвольное линейное многообразие.

Вычисление расстояния между линейными многообразиями (и некоторыми другими объектами, заданными алгебраическими уравнениями) ☞ ЗДЕСЬ.

Угол между вектором и линейным многообразием

Эта теорема сводит задачу к решенной в предыдущих пунктах задаче вычисления расстояния от вектора до подпространства, только теперь интерес смещается от ортогональной составляющей вектора к его ортогональной проекции.

Свойства матрицы Грама

Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.

Доказательство ☞ ЗДЕСЬ

Матрица Грама линейно независимой системы векторов является положительно определенной. Матрица Грама произвольной системы векторов является положительно полуопределенной.

Дальнейшие свойства матрицы и определителя Грама ☞ ЗДЕСЬ

Задачи

Источник

Материалы этого раздела составлены на основе книги

Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969

Источник

Евклидовы пространства

Определение евклидова пространства

0\quad \forall \mathbf\ne \mathbf

\forall \lambda\in \mathbb\,;\\[5pt] &\bold<4.>\quad \langle\mathbf,\mathbf\rangle>0\quad \forall \mathbf\ne \mathbf

Линейные операции над векторами евклидова пространства удовлетворяют аксиомам 1–8 линейного пространства, а операция скалярного умножения векторов удовлетворяет аксиомам 1–4 скалярного произведения. Можно сказать, что евклидово пространство — это вещественное линейное пространство со скалярным произведением. Поскольку евклидово пространство является линейным пространством, на него переносятся все понятия, определенные для линейного пространства, в частности, понятия размерности и базиса.

Простейшие следствия из аксиом скалярного произведения

1. Аксиомы 2 и 3 скалярного произведения можно заменить одним условием линейности скалярного произведения по первому сомножителю:

\forall \alpha,\beta\in \mathbb.[/math]

2. Условие линейности скалярного произведения по первому сомножителю в силу симметричности (аксиома 1) справедливо и для второго сомножителя, т.е. скалярное произведение линейно по любому сомножителю.

3. Линейность скалярного произведения по любому сомножителю распространяется на линейные комбинации векторов:

для любых векторов [math]\mathbf_i,\,\mathbf_j[/math] и действительных чисел [math]\alpha_i,\,\beta_j,

4. Если хотя бы один сомножитель — нулевой вектор, то скалярное про изведение равно нулю:

Неравенство Коши-Буняковского

Для любых векторов [math]\mathbf[/math] и [math]\mathbf[/math] евклидова пространства [math]\mathbb[/math] выполняется неравенство Коши-Буняковского :

В самом деле, для любого действительного числа [math]\lambda[/math] и любых векторов [math]\mathbf[/math] и [math]\mathbf[/math] справедливо неравенство:

Примеры евклидовых пространств

Определяя для элементов линейного пространства операцию скалярного произведения, получаем евклидово пространство. Если скалярное произведение можно ввести разными способами в одном и том же линейном пространстве, то и получаемые евклидовы пространства будут разными. Приведем примеры евклидовых пространств, соответствующих рассмотренным ранее примерам линейных пространств.

3. В пространстве [math]\mathbb^n[/math] скалярное произведение столбцов [math]x= \beginx_1&\cdots&x_n\end^T[/math] и [math]y=\begin y_1&\cdots&y_n\end^T[/math] можно задать формулой:

Значит, выполняются аксиомы 2 и 3. Аксиома 4 также выполняется, так как квадратичная форма [math]\langle x,x\rangle= x^TAx[/math] положительно определенная. Таким образом, пространство [math]\mathbb^n[/math] со скалярным произведением (8.26) является евклидовым пространством. В частности, если в качестве матрицы [math]A[/math] взять единичную матрицу, формула (8.26) примет вид:

Приведем примеры формул, которые не задают скалярного произведения в [math]\mathbb^2:[/math]

1) [math]\langle x,y\rangle= |x_1|\cdot|y_1|+|x_2|\cdot|y_2|[/math] — аксиомы 1, 4 выполняются, а аксиомы 2, 3 — нет;

2) [math]\langle x,y\rangle=x_2\cdot y_2[/math] — аксиомы 1, 2, 3 выполняются, а аксиома 4 — нет.

4. Пространство [math]\[/math] решений однородной системы [math]Ax=o[/math] линейных уравнений со скалярным произведением (8.27) является евклидовым пространством.

6. В пространстве [math]P(\mathbb)[/math] многочленов с действительными коэффициентами скалярное произведение можно задать формулой (8.28), так как многочлены являются непрерывными функциями.

В пространстве [math]P_3(\mathbb)[/math] определим произведение формулой:

В силу симметричности и линейности правой части (8.30) по значениям многочленов, заключаем, что аксиомы 1-3 выполняются. Проверим выполнение аксиомы 4. Приравняв скалярный квадрат нулю, получаем

Длина вектора и угол между векторами в евклидовом пространстве

Углом между ненулевыми векторами [math]\mathbf[/math] и [math]\mathbf[/math] евклидова пространства [math]\mathbb[/math] называется число

Из неравенства Коши-Буняковского (8.25) следует неравенство треугольника :

то есть [math]|\mathbf+\mathbf|^2\leqslant (|\mathbf|+ |\mathbf|)^2

Пример 8.17. Даны векторы евклидовых пространств:

y=\begin0\\1\end[/math] — элементы пространства [math]\mathbb^2[/math] со скалярным произведением (8.27): [math]\langle x,y\rangle=x_1y_1+x_2y_2[/math] ;

y=\begin0\\1\end[/math] — элементы пространства [math]\mathbb^2[/math] со скалярным произведением (8.26):

q(x)=x+2[/math] — элементы пространства [math]P_2(\mathbb)[/math] со скалярным произведением (8.29): [math]\langle p,q\rangle= a_2b_2+a_1b_1+a_0b_0[/math] ;

q(x)=x+2[/math] — элементы пространства [math]P_2(\mathbb)[/math] со скалярным произведением (8.30):

В каждом пространстве найти длины двух данных векторов и угол между ними.

Решение. а) Находим скалярные произведения:

б) Находим скалярные произведения:

в) Находим скалярные произведения:

г) Находим скалярные произведения:

\langle p,q\rangle= 1\!\cdot\!0+(-2)\!\cdot\!1+1\!\cdot\!2=0;

\langle q,q\rangle= 0\!\cdot\!0+1\!\cdot\!1+2\!\cdot\!2=5.[/math]

д) Находим скалярные произведения:

\langle p,q\rangle= 0\!\cdot\!3+1\!\cdot\!4+4\!\cdot\!5=24;

\langle q,q\rangle= 3\!\cdot\!3+4\!\cdot\!4+5\!\cdot\!5=50.[/math]

Источник

Трехмерный мир, в котором мы не живем

Еще древние греки превратили математику из эмпирической науки в дедуктивную, потребовав вывода доказательств ее утверждений из основных понятий и исключив ссылку на опыт в качестве аргумента.

Чистая математика исследует формы и отношения в отвлечении от материального содержания. Ее непосредственным предметом оказываются, например, не те или иные тела шарообразной формы, а «идеальный шар», не те или иные совокупности предметов и даже не отдельные числа, а целые числа вообще и т. п.

Однако при всей абстрактности этой науки никто из математиков, по-видимому, не сомневался в том, что все их понятия, теоремы и формулы выражают реальные количественные и пространственные отношения. Математическая геометрия была теорией реального пространства, как позже механика явилась теорией движения

Математика — наука, изучающая
количественные и пространственные
формы и отношения действительности
Академик А. Д. Александров

Окружающий нас мир трехмерен. Мы привыкли к этой мысли с рождения — каждый человек знает, что такое высота, длина и ширина, три основных измерения окружающего нас пространства. В зависимости от традиций, принятых в разных странах, размеры предметов измеряют в метрах, футах, ли, лье и других эталонных единицах длины. Для наших дальнейших рассуждений выберем немного необычную единицу длины. Ею будет служить один световой год (1 св. г.), т. е. расстояние, проходимое лучом света за один календарный год. В традиционных мерах длины это составляет невообразимую величину — примерно 9,46•10 12 километров.

Если из окружающего нас пространства мысленно вырезать куб с ребром, равным 1 св. году, то внутри благополучно разместится дом, в котором мы живем, земной шар, Солнечная система… В общем, все, что необходимо для нормальной жизни человека. Для удобства назовем рассмотренный нами куб единичным кубом. А теперь отметим следующий очевидный факт. Несмотря на громадные размеры, наш единичный куб — лишь мельчайшая частица окружающего мира.

Кстати сказать, в этом определении размеры самого куба не задаются — вовсе не обязательно использовать кубы больших размеров. С таким же успехом можно утверждать, что каждая точка содержится в кубе, ребро которого не превосходит по длине, скажем, один микрон (10 —6 см).

Все сказанное выше кратко можно выразить следующими словами: окружающий нас мир является трехмерным евклидовым многообразием. А теперь попробуем ответить на следующий вопрос: как устроен мир за пределами единичного куба, в котором находится наш дом — наша Солнечная система?

Трехмерный тор и другие

Если на минуту вообразить, что окружающее нас пространство бесконечно по всем направлениям, то ответ на вопрос о строении окружающего нас мира даст следующая теорема Адамара:

«Бесконечно протяженное по всем направлениям трехмерное евклидово многообразие М 3 совпадает с евклидовым пространством E 3 ».

Евклидово пространство Е 3 с прямоугольной системой координат всем хорошо известно, поэтому не будем подробно останавливаться на изучении его свойств.

Для того же, чтобы сделать наши рассуждения более содержательными и интересными, предположим другой вариант: окружающий нас мир замкнут, т. е. имеет конечные размеры и не имеет края. Другими словами, зададимся вопросом, как устроены замкнутые трехмерные евклидовы многообразия, или, другими словами, евклидовы формы. Полный ответ на этот вопрос дает теорема, доказанная Дж. Вольфом (1982):

Существует ровно десять трехмерных евклидовых форм. Причем шесть из них представляют собой ориентируемые, а остальные четыре — неориентируемые многообразия.

Все евклидовые формы строятся схожим образом, единственное — для построения некоторых из них нужно использовать куб, а для других — правильную шестиугольную призму.

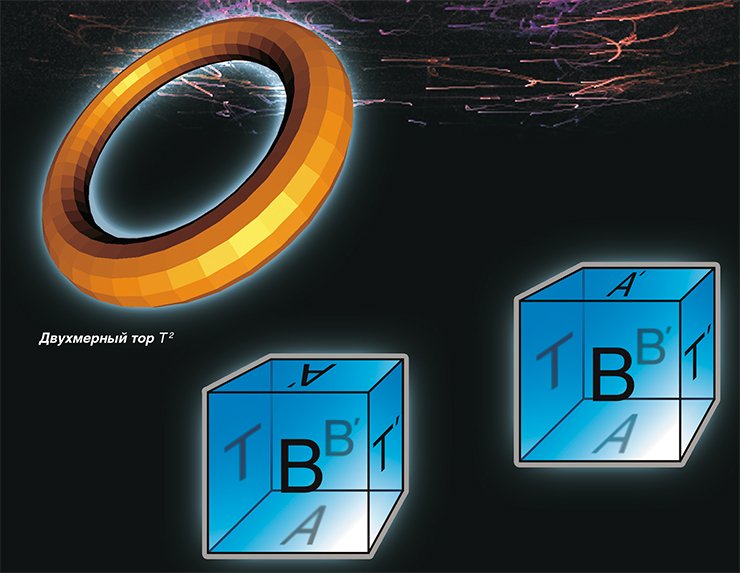
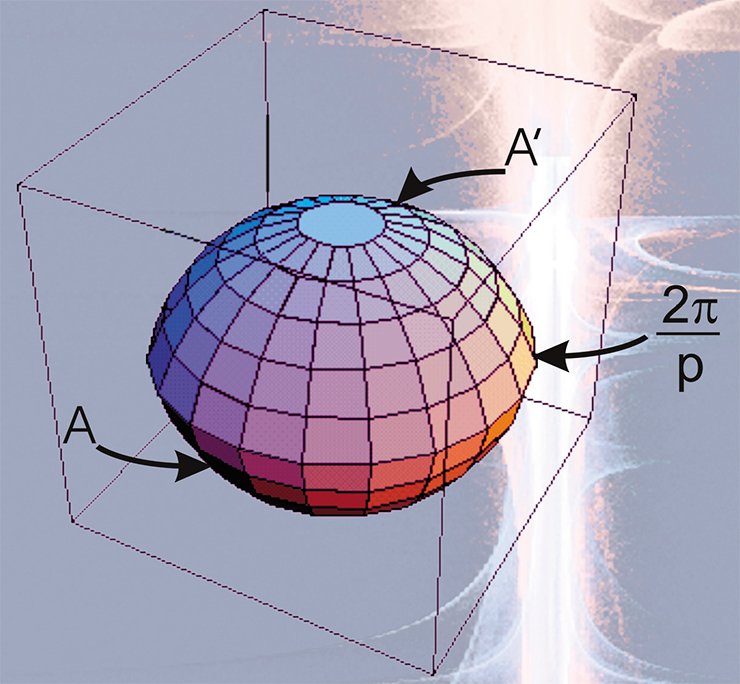
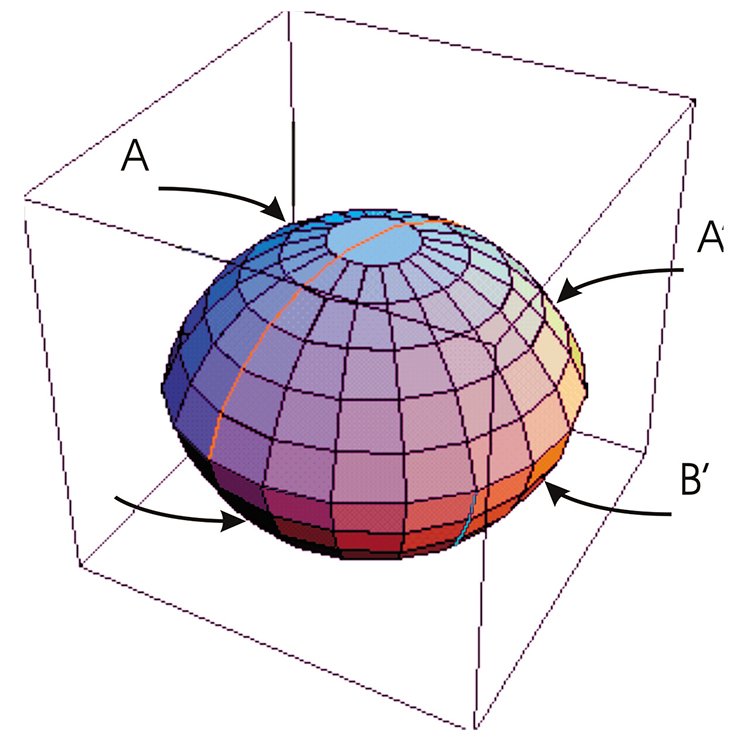
Для этого в центре грани А трехмерного тора поместим космический корабль, летящий со скоростью света, и заставим его стартовать в вертикальном направлении. Ровно через год космический корабль, продолжая двигаться по прямой, вернется в исходную точку. Теперь эта точка будет находиться в центре грани А’, которая, по условию, отождествлена с гранью А. В результате эксперимента обнаружим, что в трехмерном торе Т 3 существует замкнутая прямая линия l длиной в один световой год.

Поставим еще один аналогичный эксперимент. Заставим космический корабль стартовать из точки у, лежащей в грани А на расстоянии 1 км от ее центра. Через год корабль благополучно вернется в точку у. Вывод из второго эксперимента — через точку у проходит замкнутая прямая длиной 1 световой год, параллельная прямой l.

Многообразные многообразия

Как уже было замечено, все рассмотренные выше многообразия обладают евклидовой геометрией. Что это означает и какие еще геометрии существуют?

Наиболее известными и употребимыми в общечеловеческой практике являются евклидова, сферическая и гиперболическая геометрии. Напомним, что сферическую геометрию иногда называют геометрией Римана, а гиперболическую — геометрией Лобачевского. В трехмерном пространстве, кроме трех указанных, существует еще пять так называемых синтетических геометрий.

В соответствии с тем, какие геометрические законы действуют на трехмерном многообразии, будем называть его соответственно евклидовым, сферическим, гиперболическим или синтетическим.

Евклидовы многообразия мы уже рассмотрели выше. Что до остальных, то более двадцати лет назад У. Терстон (1978) доказал замечательную теорему: почти все трехмерные многообразия являются гиперболическими, то есть подчиняются законам геометрии Лобачевского. За этот результат в 1983 году он был удостоен Филдсовской премии — самой престижной награды для математиков.

Сферические многообразия бывают как трехмерные, так и многомерные (Вольф, 1982). В пространстве любой размерности существует конечное число типов таких многообразий. Синтетических многообразий очень мало (Thurston, 1978; Dunbar, 1981; Терстон, 2001) в отличие от оставшегося класса гиперболических многообразий. Последний неисчерпаемо широк и классификация его к настоящему времени не завершена.

Сферические многообразия

Все трехмерные сферические многообразия — ориентируемы. Это означает, что по какой бы замкнутой траектории не летал космический корабль с непрерывно вращающимся пропеллером, по возвращении в точку старта его пропеллер вращается в ту же сторону, что и в момент старта.

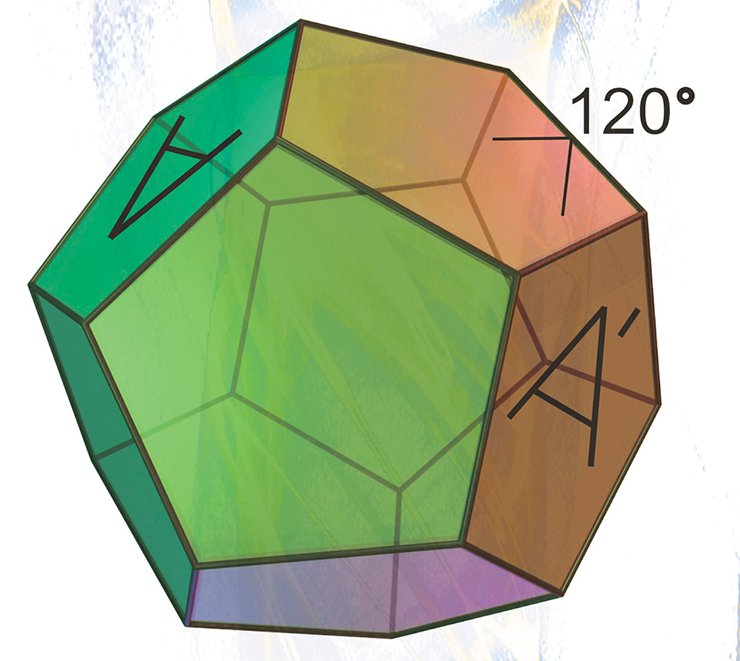
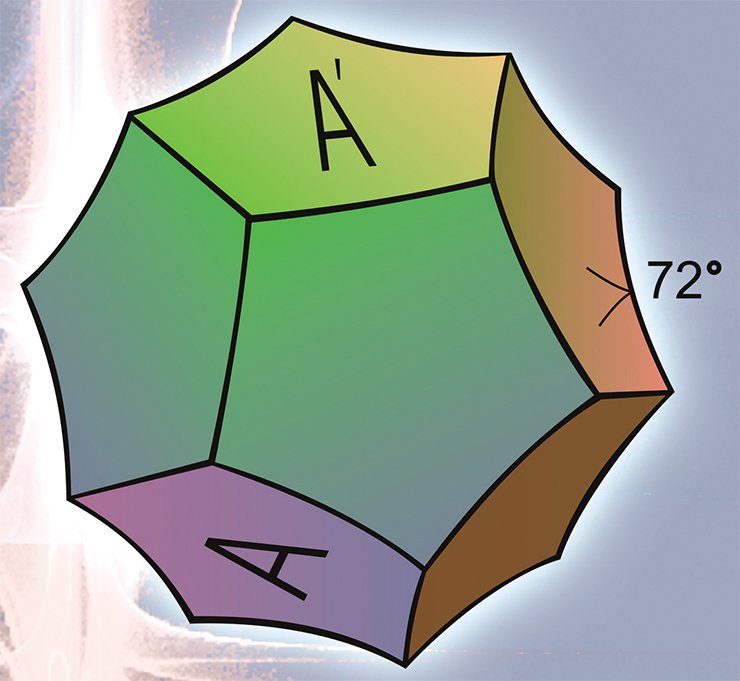
Третий, и пожалуй, самый нетривиальный пример сферического многообразия — сферическое пространство додекаэдра Пуанкаре или, для краткости, сфера Пуанкаре.

Сфера Пуанкаре удивительным образом связана с самыми различными разделами математики — геометрией, топологией, теорией групп, теорией катастроф, теорией узлов и другими (Кирби, Шарлеман, 1982).

Все остальные сферические многообразия, получаемые по единой схеме, представляют собой так называемые линзовые и призматические пространства.

Гиперболические многообразия

Первое трехмерное замкнутое гиперболическое многообразие было построено немецким математиком Ф. Лебеллем в 1931 г. Однако построение его было достаточно сложным, поэтому двумя годами позже Х. Зейферт и К. Вебер предложили элегантную конструкцию гиперболического пространства додекаэдра.

С точки зрения математики наиболее сложная часть проблемы построения состоит в доказательстве существования этого гиперболического додекаэдра в пространстве Лобачевского. Положительный ответ на этот вопрос дает фундаментальная теорема Е. М. Андреева (1970), в которой сформулированы необходимые и достаточные условия для существования выпуклых гиперболических многогранников. Эта теорема служит одним из краеугольных камней современной теории гиперболических многообразий, созданной У. Терстоном.

Конструируем многообразия из многогранников

Рассмотрим прямоугольный многогранник Р, все двугранные (и плоские) углы которого равны 90°. В евклидовом пространстве в качестве такого многогранника можно взять куб, в сферическом — тетраэдр, а в гиперболическом — шестиугольную призму Лебелля, боковая поверхность которой состоит из 12-ти пятиугольников.

Из теоремы Андреева следует, что любой многогранник, у которого нет треугольных и четырехугольных граней, а в каждой вершине сходится ровно по три ребра, может быть реализован как прямоугольный многогранник в пространстве Лобачевского. Шестиугольная призма Лебелля, очевидно, удовлетворяет этим условиям.

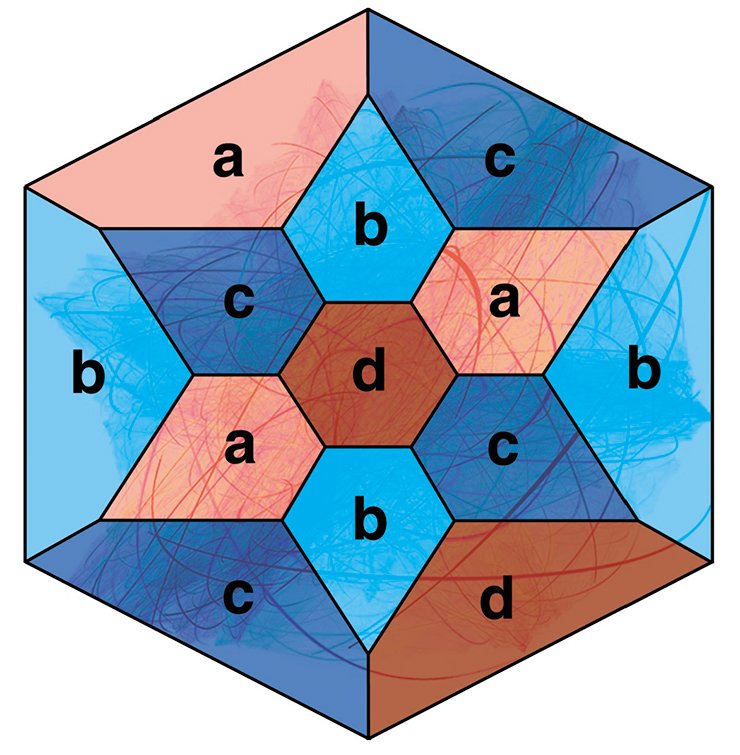
Для построения гиперболических многообразий используется способ, заключающийся в окраске смежных граней многогранника в разные цвета и последующего отождествления соответствующих граней, окрашенных в один цвет, у нескольких одинаковых экземпляров многогранников. Такой способ построения многообразий был впервые реализован Ф. Лебеллем (Loebell, 1931) для шестиугольной призмы, японским математиком М. Такахаши (Takahashi, 1985) — для правильного прямоугольного додекаэдра и А. Ю. Весниным (1987) — для произвольного прямоугольного многогранника Р.

При этом отметим, что все многообразия, построенные по окраске многогранника в четыре цвета, ориентируемы. Однако доказано, что окрашивая грани многогранника Р в пять, шесть или семь цветов, по аналогичной схеме можно построить и неориентируемые многообразия (Mednykh, 1992).

Остановимся еще на одном свойстве прямоугольных многогранников. Пусть D — правильный прямоугольный додекаэдр в пространстве Лобачевского. Испанский математик Х.-М. Монтезинос (Hilden et al., 1987) доказал следующую замечательную теорему:

«Любое замкнутое трехмерное многообразие может быть получено из конечного числа экземпляров многогранника D попарным отождествлением их граней».

Отметим, что в теореме Монтезиноса все грани склеенных многогранников — конгруэнтны, а все ребра имеют одинаковую длину. При этом каждое ребро окружено четырьмя, двумя или одним додекаэдром. Первую ситуацию легко представить: четыре прямоугольных додекаэдра склеены друг за другом вокруг общего ребра и образуют суммарный угол, равный 4•90° = 360°. Во втором случае пара смежных граней одного додекаэдра отождествляется с парой смежных граней другого додекаэдра. Суммарный двугранный угол вокруг ребра, принадлежащего двум додекаэдрам, в этом случае равен 2•90° = 180°. Третий вариант легко создать, отождествляя смежные грани одного додекаэдра поворотом на угол 90°.

Наличие ребер второго и третьего типа превращает многообразие в многообразие с особенностями, или орбифолд. В этом случае указанные ребра образуют сингулярное множество орбифолда. Заметим, что всюду, кроме сингулярных ребер, многообразие обладает геометрией Лобачевского.

Трехмерные орбифолды

Евклидовы орбифолды

Для всякого трехмерного евклидова орбифолда существует фундаментальное множество — криволинейный многогранник, из которого заданный орбифолд можно получить, попарно отождествляя (склеивая) определенные его грани.

Примерами евклидовых орбифолдов могут служить так называемые Борромеевы кольца или трехмерная сфера с сингулярным множе­ством узел «восьмерка».

Всего существует 230 замкнутых трехмерных евклидовых орбифолдов — по числу кристалло­графических групп, открытых в конце прошлого века русским ученым Е. С. Федоровым. Строение евклидовых орбифолдов было полностью описано в докторской диссертации У. Данбара, защищенной в 1981 г. в Принстонском университете — крупнейшем математическом центре мира.

Сферические орбифолды

Сингулярным множеством сферических орбифолдов может служить так называемый рациональный узел или зацепление. Им может оказаться также заузленный граф, из каждой вершины которого выходит по три ребра. В частности, сингулярным множеством сферического орбифолда будет являться скелет тетраэдра (ребра + вершины), расположенный в трехмерной сфере.

q > l. В сферическом пространстве S ³ рассмотрим линзу с углом, равным π/р и поделим ее ребро точками 1,2. 2р на 2р равных частей. Соединим пары точек <р, 2р>и сферическими дугами, лежащими по разные стороны линзы. Поворотами на 180° в построенных дугах отождествим половины граней линзы A,A’ и B,B’. В случаях p/q = 2/1 мы получим, соответственно, зацепление Хопфа, состоящее из двух сцепленных окружностей; в случае p/q = 3/1 — узел «трилистник»; при p/q = 5/3 — уже описанный узел «восьмерка»» border=»0″ alt=»Пусть p/q — несократимая дробь с условием p > q > l. В сферическом пространстве S ³ рассмотрим линзу с углом, равным π/р и поделим ее ребро точками 1,2. 2р на 2р равных частей. Соединим пары точек <р, 2р>и сферическими дугами, лежащими по разные стороны линзы. Поворотами на 180° в построенных дугах отождествим половины граней линзы A,A’ и B,B’. В случаях p/q = 2/1 мы получим, соответственно, зацепление Хопфа, состоящее из двух сцепленных окружностей; в случае p/q = 3/1 — узел «трилистник»; при p/q = 5/3 — уже описанный узел «восьмерка»» />

При этом следует иметь ввиду, что сильные заузливания тетраэдра могут испортить сферическую геометрию и заставить орбифолд обладать евклидовой, гиперболической или одной из синтетических геометрий.

Недавно австралийцами профессором К. Ходжсоном и его учеником Д. Хеардом создана компьютерная программа, позволяющая вычислять объемы заузленных графов, вложенных в трехмерную сферу (Hodgson and Heard, 2005). Полная классификация трехмерных орбифолдов во всех геометриях, кроме гиперболической, сделана в работах У. Данбара. Как и в случае многообразий, гиперболическая геометрия является наиболее богатой, и полное описание орбифолдов в ней до сих пор не получено.

Гиперболические орбифолды

Из теоремы Монтезиноса следует, что каждое трехмерное многообразие может быть превращено в гиперболический орбифолд, если внутрь его поместить подходящее сингулярное множество. Поскольку существует бесконечно много различных многообразий, отсюда следует, что существует также бесконечно много гиперболических орбифолдов.

Один из простейших гиперболических орбифолдов — трехмерная сфера с сингулярным множеством Борромеевы кольца с индексом сингулярности 4. Другой пример — сильно заузленный тетраэдр, все ребра которого имеют индекс сингулярности два. Доказательство таких фактов обычно достаточно сложно и может быть проведено с помощью теорем о геометризации, полученных У. Терстоном, его учениками и последователями. Общий принцип доказательства состоит в следующем: если орбифолд не является евклидовым, сферическим или синтетическим и удовлетворяет некоторым простым геометрическим условиям, то он — гиперболический.

Изменения, произошедшие в математике за последние более чем полтора века, не только необозримо расширили ее содержание, но и изменили его принципиально. В предмет математики сейчас входит любая структура, которую можно исследовать путем логического рассуждения с достаточной строгостью и богатством выводов. Найдет ли она применение и прообраз в действительности — это уже вопрос не к математике.

Понятно, что фактически наибольшее развитие получают те теории, которые находят существенные применения в самой математике и тем более за ее пределами. Хотя опыт развития науки уже достаточное число раз показал, как самые отвлеченные теории находили потом чрезвычайно существенные приложения. Но для самой чистой математики это в принципе безразлично. Лучше всего творческое кредо новой математики выразил создатель теории множеств Г. Кантор, гордо зявив: «Сущность математики. в ее свободе».

Винберг Э. Б. О неевлидовой геометрии, Соросовский образовательный журнал, № 3, 1996, С. 104—109.

Тёрстон У. Трехмерная геометрия и топология, М: МЦНМО, 2001 (Перевод с англ. под ред. О. В. Шварцмана).

Hodgson C., Heard D. Computer program “Orb”, August 2005, http://www.ms.unimelb.edu.au/

Работа поддержана грантом РФФИ (№ 06-01-00153) и INTAS (№ 03-01-3663)

Автор и редакция выражает искреннюю благодарность Н. В. Абросимову (вед. инженеру Института математики им. С. Л. Соболева СО РАН, студенту 6-го курса НГУ), оказавшему неоценимую помощь при подготовке публикации

Источник