Как сделать поверхность в excel
Excel 3D Plot
Excel 3D Plot (Содержание)
3D-график в Excel
Как построить 3D-графики в Excel?
Построение 3D-графиков в Excel очень просто и полезно, когда мы хотим преобразовать данные, круговые диаграммы, графики в 3D-формат. Давайте разберемся, как строить 3D-графики в Excel на нескольких примерах.
Доступ к 3D-графику можно получить из меню « Вставка» в разделе «Графики ».
У нас есть данные о том, где мы измерили расстояние, пройденное некоторыми спортсменами в метрах. Расстояние покрыто экземпляром почасовой оплаты. В течение 5 часов каждый спортсмен преодолевал некоторую дистанцию, и в конце наибольшего пройденного расстояния он выигрывает игру. Таким образом, увидев данные, мы можем не прийти к выводу или даже не можем сравнить. Если мы нанесем эти данные на трехмерные графики, то будет легко проверить ситуацию.
Теперь создаем 3D-график для вышеуказанного набора данных, сначала выберите данные.
Затем перейдите на вкладку меню Вставка и под диаграммой выберите столбчатую диаграмму. Как только мы нажмем на него, мы получим раскрывающееся меню. Оттуда выберите 3D-столбец, как показано ниже.
После выбора опции 3D Column мы получим трехмерный график с колонкой, как показано ниже. Здесь мы можем добавить метки данных, заголовки осей, заголовок и даже изменить дизайн 3D-столбцов.
Как видно из приведенного выше графика, все данные отображаются в столбцах, и эти столбцы параллельно обрамлены данными. Высота столбцов сопоставлена, а параметры высоты показаны выше для каждого столбца.
Давайте снова отобразим эти данные на другом трехмерном графике. Теперь мы будем строить 3D-график. Для этого сначала выберите данные, а затем перейдите на вкладку меню « Вставка », в разделе «Диаграммы» выберите « Водопад», «Фондовая», «Поверхность» или «Радар», как показано ниже. (И для других версий Excel выберите опцию Other Charts )
Как только мы это сделаем, мы получим 3D-график поверхности, как показано ниже.
Приведенные выше данные показывают расстояние, пройденное атлетами по гребню и впадине, а область разного цвета представляет диапазон расстояний. Таким образом, мы можем попробовать еще несколько 3D-графиков, доступных в Excel, в соответствии с нашим использованием.
Теперь для построения трехмерного графика для приведенного выше примера сначала выберите полные данные. Затем перейдите в меню «Вставка» и в разделе «Графики» выберите столбчатую диаграмму, как показано ниже. Как только мы нажмем на него, мы получим раскрывающееся меню. Оттуда выберите 3D-столбец, как показано ниже.
После выбора опции 3D Column мы получим трехмерный график с колонкой, как показано ниже.
Как мы видим, здесь есть несколько огромных башен и несколько плоских блоков. Построение данных такого рода в трехмерных диаграммах дает возможность увидеть, где в процессе наблюдаются пики и спады. Мы можем добавить метки данных здесь.
Давайте построим еще один 3D-график на тех же данных. Для этого выберите данные и перейдите в меню «Вставка», в разделе «Диаграммы» выберите « Линия» или « Диаграмма площади», как показано ниже.
После этого мы получим выпадающий список линейных графиков, как показано ниже. Оттуда выберите 3D Line chart.
После нажатия на него мы получим график графика 3D Line, как показано ниже.
Это самый выполнимый, простой 3D-сюжет. И это очень легко понять. Поскольку данные в этом сюжете достаточно разделены друг с другом. И изменения в данных также хорошо видны. Использование графика 3D Line хорошо, когда у нас есть данные, где мы можем легко увидеть разделение.
Выше приведен пример некоторых из категории 3D-графики. Мы можем создать трехмерный график для круговой диаграммы, диаграммы площади, линейчатой диаграммы и комбинированной диаграммы, если имеющиеся у нас данные позволяют нам по-разному представлять требуемые виды.
Если мы создадим круговую диаграмму для данных, которые мы рассмотрели для приведенных выше примеров, то мы не сможем получить желаемый вид на трехмерном графике. Поэтому лучше сначала понять, что мы хотим видеть, а затем мы можем сопоставить его с желаемым трехмерным графиком.
Плюсы 3D-сюжета в Excel
То, что нужно запомнить
Рекомендуемые статьи
Диаграмма поверхности в Excel
Диаграмма поверхности Excel (график)
Поверхностная диаграмма — это трехмерная диаграмма Excel, на которой точки данных отображаются в трех измерениях. Вы можете видеть сетку поверхности, которая помогает нам найти оптимальную комбинацию между двумя типами точек данных. Типичная поверхностная диаграмма состоит из трех переменных точек данных, назовем их «X, Y и Z». Из этих трех доступных переменных мы можем разделить их на два набора, то есть независимые и зависимые переменные. Две переменные будут независимыми переменными, а одна — зависимой переменной.
Таким образом, диаграмма поверхности показывает взаимосвязь между точками данных через поверхность сетки.
Примеры создания диаграммы поверхности (графика) в Excel
Пример # 1
Рассмотрите приведенные ниже данные, чтобы создать свою первую диаграмму поверхности в Excel.
Выполните следующие шаги, чтобы создать поверхностную диаграмму в Excel.
Шаг 1: Сначала откройте электронную таблицу Excel.
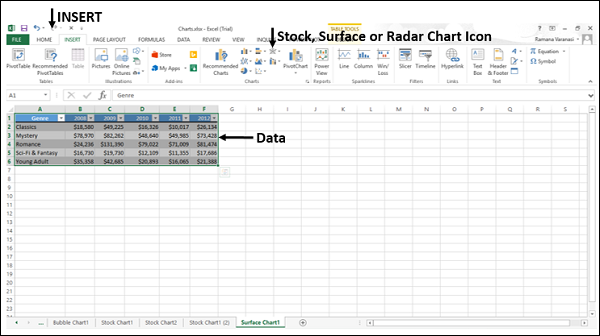
Шаг 2: Скопируйте приведенную выше таблицу данных на один из рабочих листов. И выберите диапазон данных.
Шаг 3: Теперь на вкладке ленты выберите опцию «ВСТАВИТЬ».
Шаг 4: На вкладке INSERT вы можете увидеть раздел «Диаграмма». В этом разделе в Excel выберите Stock, Surface или Radar Chart. В этой категории диаграмм выберите «3D-поверхность» диаграмма.
Шаг 5: Как только вы нажмете на «3D-диаграмму поверхности», вы увидите приведенную ниже диаграмму поверхности по умолчанию на своем рабочем листе.
Шаг 6: Это не окончательная поверхностная диаграмма конечного пользователя. Нам нужно настроить диаграмму, чтобы это было лучше видно.
Шаг 7: В этой ОБЛАСТИ ФОРМАТИРОВАНИЯ ДИАГРАММЫ вы можете изменить цвет сетки, настройку горизонтальной и вертикальной оси, а также многое другое.
Чтобы изменить цвет сетки, вы можете сделать это на самой вкладке ДИЗАЙН. Выбрав диаграмму, вы увидите две вкладки «Работа с диаграммами», то есть «Дизайн и формат».
Выберите вкладку «Дизайн», перейдите в «Изменить цвет» и выберите цвет по своему усмотрению.
Как видите, я выбрал четвертый, и я вижу предварительный просмотр моей диаграммы с правой стороны. Как и в этом месте, курсор на каждом из разных наборов цветов для предварительного просмотра диаграммы перед окончательной комбинацией цветов.
Шаг 8: Следующее, что нам нужно сделать, это «Переключить строку / столбец». Поскольку во время вставки диаграммы Excel предполагает, что горизонтальные объекты — это ряды данных, а вертикальные — категории.
Поэтому нам нужно изменить строку / столбец на вкладке «Дизайн».
Как только вы выберете эту опцию, наша диаграмма изменится автоматически, и теперь она выглядит так, как показано ниже.
Пример # 2
Теперь давайте посмотрим еще на один пример Surface Chart. Для этого рассмотрим набор данных ниже.
Скопируйте данные на рабочий лист.
Выбрав данные, выберите опцию вставки диаграммы.
Теперь мы можем видеть диаграмму ниже.
Теперь на вкладке «Дизайн» выберите «Быстрый макет» и выберите «Макет 5».
Теперь наша диаграмма выглядит так.
Таким образом, мы можем создать в Excel сетчатую диаграмму поверхности.
Диаграммы Excel — Поверхностная диаграмма
Поверхностные диаграммы полезны, когда вы хотите найти оптимальные комбинации между двумя наборами данных. Как и на топографической карте, цвета и узоры указывают области, которые находятся в одном диапазоне значений.
Чтобы создать диаграмму поверхности, убедитесь, что категории и серии данных являются числовыми значениями.
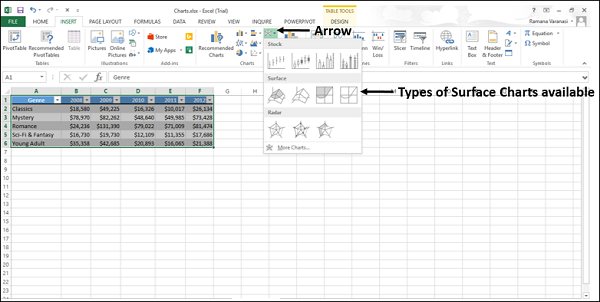
Шаг 1 — Расположите данные в столбцах или строках на листе.
Шаг 2 — Выберите данные.
Шаг 3 — На вкладке ВСТАВИТЬ в группе Диаграммы щелкните значок Лента, Поверхность или Радар на ленте.
Вы увидите различные типы доступных карт поверхностей.
Диаграмма поверхности имеет следующие подтипы —
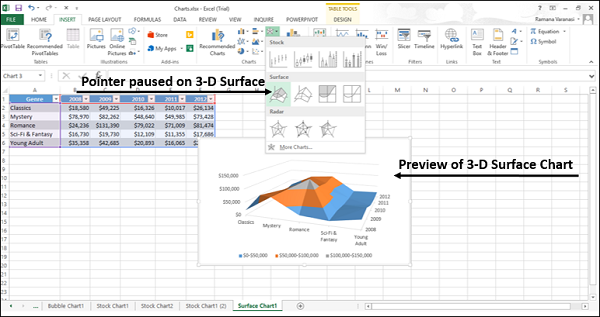
Шаг 4 — Наведите указатель мыши на каждый из значков. Предварительный просмотр этого типа диаграммы будет показан на листе.
Шаг 5 — Дважды щелкните тип диаграммы, который соответствует вашим данным.
В этой главе вы поймете, когда каждый из типов диаграмм Surface полезен.
3-D поверхность
Трехмерная диаграмма поверхности показывает трехмерное представление данных, которое можно представить в виде резинового листа, натянутого на трехмерную диаграмму столбца. Обычно он используется для отображения взаимосвязей между большими объемами данных, которые в противном случае может быть трудно увидеть.
Поверхностная диаграмма в Excel и пример ее построения
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
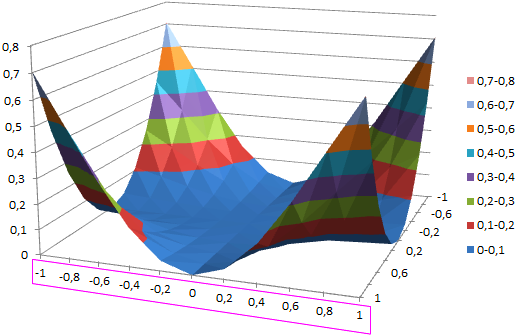
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
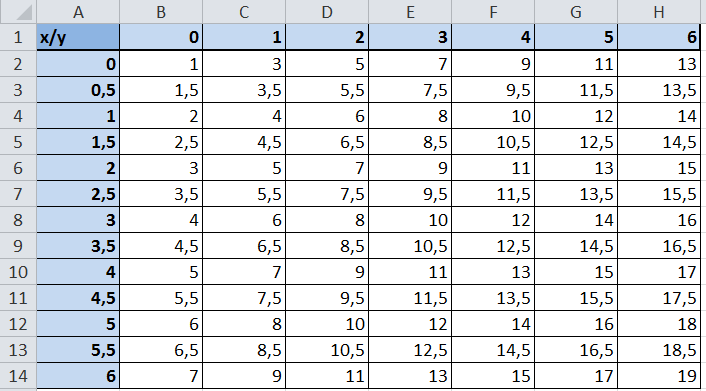
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
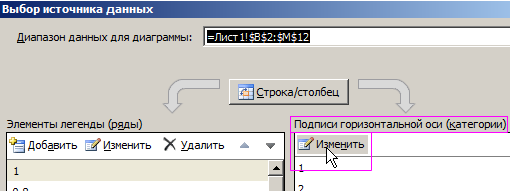
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
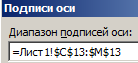
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
Построение поверхностей второго порядка в excel
Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.
Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.
В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение
определяет плоскость, проходящую через начало координат.
Если А=О, то уравнение
определяет плоскость, параллельную оси Ох; если А=D =, то уравнение
определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение
определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение
Cz = 0 (или z = 0) определяет координатную плоскость Оху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:
где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку 
В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.
Пример1. Рассмотрим построение плоскости в Excel на примере уравнения 
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
В результате должна быть получена следующая таблица (рис. 1).
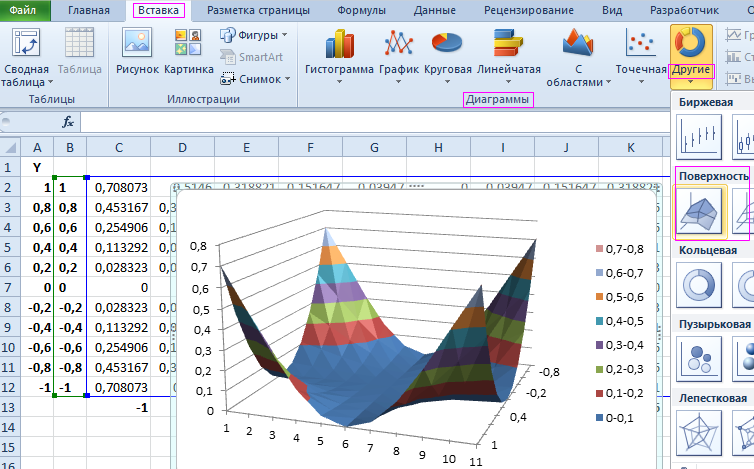
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведите вид получившейся диаграммы как показано на рисунке:
Упражнения
1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.
2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.
3. Построить плоскость, проходящую через точки М(3,3,1), М2(2,3,2), М3(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.
Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.
Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.
Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
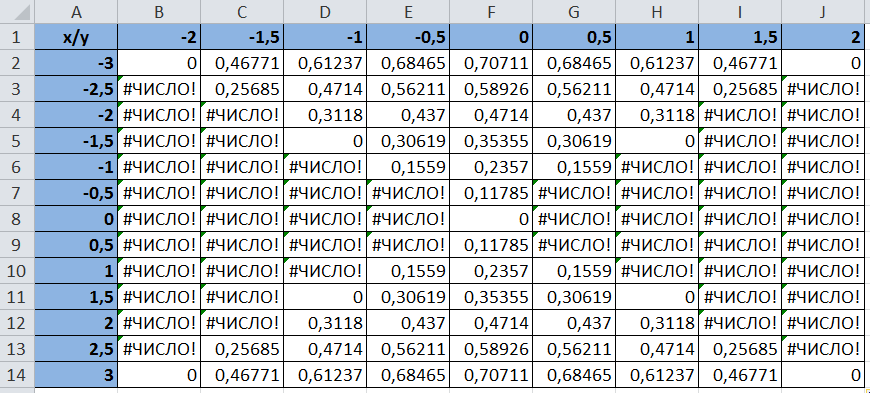
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример3. Рассмотрим построение двухполостного гиперболоида вида
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Пример 4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.
В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.
Упражнения
1. Построить верхнюю часть эллипсоида:
Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.
2. Построить верхнюю часть однополостного гиперболоида:
Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.
3. Построить эллиптический параболоид:
Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.
4. Построить верхнюю часть конуса
Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.
| | | следующая лекция ==> |
| | | Решите задачи с использованием диаграммы Эйлера-Венна. |
Дата добавления: 2017-02-25 ; просмотров: 2062 | Нарушение авторских прав
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
by Ирина Кяршис
ГЛАВА 1. Возможности табличного процессора Microsoft Excel
1.1.Ввод данных в Excel
Электронная таблица – это программа, позволяющая автоматизировать табличные расчеты. Документ Microsoft Ехсел является рабочей книгой, состоящей из листов. Таблица состоит из 65536 строк и 256 столбцов. Строки нумеруются числами, столбцы – буквами латинского алфавита (А, В …, Z, АА, АВ …). На пересечении строки и столбца расположена ячейка, которая имеет адрес, состоящий из имени столбца и номера строки (А4). Одна из ячеек всегда является активной.
Прямоугольная группа смежных ячеек называется диапазоном ячеек. Примеры диапазонов – А2: С4, В2: К40.
Ячейки могут содержать данные трех типов:
1) Текстовые данные – это строка текста произвольной длины.
2) Числовые данные – это отдельное число. Может быть целым, дробным (зап.). Если ширина ячейки мала, то число записывается в экспоненциальной форме, например 125 000 000 → 1,25Е + 8 или вместо числа ставятся символы ###. При этом число сохраняется.
Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.
1.2.Типы диаграмм
В зависимости от типа диаграммы данные отображаются на ней разным способом.
Можно отметить несколько стандартных типов:
Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.
Подробнее о типах диаграмм здесь
1.3 Основы построения диаграмм в Excel
Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.
Совокупность этих элементов определяет макет диаграммы.
Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).
Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.
Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.
ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2.1 Уравнения поверхностей второго порядка и их графики
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.
Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.
Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=1, где a и b – действительные полуоси, с – мнимая полуось.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=-1,где с – действительная полуось, a и b – мнимые полуоси.