Как сделать поверхность в матлабе
Иллюстрированный самоучитель по MatLab
Построение поверхности с окраской
Особенно наглядное представление о поверхностях дают сетчатые графики, использующие функциональную закраску ячеек. Например, цвет окраски поверхности z(x, у) может быть поставлен в соответствие с высотой z поверхности с выбором для малых высот темных тонов, а для больших – светлых. Для построения таких поверхностей используются команды класса surf (…):
Команды axis, caxis, color-map, hold, shading и view задают координатные оси и свойства поверхности, которые могут использоваться для большей эффектности показа поверхности или фигуры.
Ниже приведен простой пример построения поверхности – параболоида:
Соответствующий этому примеру график показан на рис. 6.25.

Рис. 6.25. График параболоида с функциональной окраской ячеек
Можно заметить, что благодаря функциональной окраске график поверхности гораздо более выразителен, чем при построениях без такой окраски, представленных ранее (причем даже в том случае, когда цветной график печатается в черно-белом виде).
В следующем примере используется функциональная окраска оттенками серого цвета с выводом шкалы цветовых оттенков:
В этом примере команда colormap(gray) задает окраску тонами серого цвета, а команда shading Interp обеспечивает устранение изображения сетки и задает интерполяцию для оттенков цвета объемной поверхности. На рис. 6.26 показан вид графика, построенного в этом примере.

Рис. 6.26. График поверхности с функциональной окраской серым цветом
Обычно применение интерполяции для окраски придает поверхностям и фигурам более реалистичный вид, но фигуры каркасного вида дают более точные количественные данные о каждой точке.
Как сделать поверхность в матлабе
Обычная графика MATLAB
Построение графиков точками и отрезками прямых
Графики в логарифмическоми полулогарифмическом масштабе
Гистограммы и диаграммы
Графики специальных типов
Создание массивов данных для трехмерной графики
Построение графиков трехмерных поверхностей, сечений и контуров
Средства управления подсветкой и обзором фигур
Средства оформления графиков
Одновременный вывод нескольких графиков
Управление цветовой палитрой
Окраска трехмерных поверхностей
Двумерные и трехмерные графические объекты
Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.
Описанию графических функций и команд посвящена обширная электронная книга в формате PDF. Объем материала по графике настолько велик, что помимо вводного описания графики в уроке 3 в этой книге даются еще два урока по средствам обычной и специальной графики. Они намеренно предшествуют систематизированному описанию большинства функций системы MATLAB, поскольку графическая визуализация вычислений довольно широко используется в последующих материалах книги. При этом графические средства системы доступны как в командном режиме вычислений, так и в программах. Этот урок рекомендуется изучать выборочно или выделить на него не менее 4 часов.
Построение графиков отрезками прямых
Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.
Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.
plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
Приведенный ниже пример иллюстрирует построение графиков двух функций — sin(x) и cos(x), значения функции которых содержатся в матрице Y, а значения аргумента х хранятся в векторе X:
На рис. 6.1 показан график функций из этого примера. В данном случае отчетливо видно, что график состоит из отрезков, и если вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.
Рис. 6.1. Графики двух функций в декартовой системе координат
plot(Y) — строит график у(г), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y). imag(Y)). Во всех других случаях мнимая часть данных игнорируется.
Вот пример использования команды plot(Y):
Соответствующий график показан на рис. 6.2.
Рис. 6.2. График функции, представляющей вектор Y с комплексными элементами
plot(X.Y.S) — аналогична команде plot(X.Y), но тип линии графика можно задавать с помощью строковой константы S.
Значениями константы S могут быть следующие символы.
Построение трехмерных графиков в MATLAB
Построение трехмерных графиков в MATLAB.
График функции двух переменных в MATLAB – это поверхность, расположенная над областями определения функции. Поэтому для прорисовки такого графика требуется использование трехмерного изображения.
Простейшим инструментом, способным отобразить график функции дыух переменных, является
plot3( X, Y, Z )
где X, Y и Z – матрицы со значениями функции (точками z) в наборах (x, y).
В системе MATLAB имеется специальная функция для получения двумерных массивов X и Y по одномерным массивам x, y.
В MATLAB существует функция построения двумерных массивов X и Y по одномерным x, y.
Пусть по оси x задан вектор
а по оси y диапазон
Для получения матриц X и Y, содержащих значения точек в этой прямоугольной сетке, используется функция:
[ X, Y ] = meshgrid( u, v )
Вычислим теперь на полученной прямоугольной сетке значение функции exp:
Теперь применим функцию plot3, которая была описана выше, и получим следующий график:
Чтобы построить трехмерные линии, заданные параметрически, применяется другая форма вызова функции plot3:
plot3( x, y, z )
Следующий пример позволяет построить винтовую линию:
t = 0 : pi/50 : 10*pi ;
x = sin( t );
y = cos( t );
plot3( x, y, t );
grid on
Причем следует отметить, что функции по обработке графиков, допустимые в двумерном случае, работают и для трехмерных изображений.
Кроме этой простейшей функции построения графиков в MATLAB есть набор инструментов, позволяющий сделать отображаемые объекты более наглядными. Это функции mesh, surf и surfl.
Функция mesh соединяет вычисленные соседние точки поверхности графика отрезками прямых и показывает в графическом окне системы MATLAB плоскую проекцию такого объёмного «каркасно-ребристого» ( по-английски зовётся wireframe mesh) тела. Вместо ранее показанного при помощи функции plot3 графика функции
Mesh соединяет соседние вычислительные точки отрезками, причем невидимые линии при отображении скрываются. Если же такие линии для отображения необходимы, нужно воспользоваться командой.
Для примера рассмотрим использование функции mesh в случае построения того же графика функции
позволяет получить следующее изображение, представляющее собой поверхность, а не набор линий.
Раскрашивание отдельных элементов поверхности в этом случае производится автоматически. Если же раскрасить их необходимо по-другому, лучше всего воспользоваться функцией surfl.
Эта функция воспринимает построенную поверхность как материальную, обладающую определенными свойствами. По умолчанию она задает некоторый источник света, после чего рассчитывает траектории отраженных от поверхности лучей. Таким образом, если задать условные параметры материала поверхности, например:
colormap( copper ) ,
то есть набор цветов (colormap), соответствующий меди (copper), то после вызова функции
surfl( X, Y, Z )
мы получим следующий график:
Убрать черные линии и добиться более лпавного света позволяет команда
Документация
Представление данных как поверхность
Функции для графического изображения сеток данных
MATLAB ® графика задает поверхность z-координатами точек выше прямоугольной сетки в x-y плоскости. График формируется путем присоединения смежных точек с прямыми линиями. Объемные поверхностные диаграммы полезны для визуализации матриц, которые являются слишком большими, чтобы отобразиться в числовой форме и для функций построения графика двух переменных.
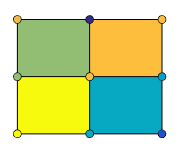
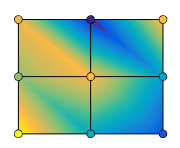
MATLAB может создать различные формы объемных поверхностных диаграмм. Сетчатые графики являются каркасными поверхностями, которые окрашивают только линии, соединяющие определяющие точки. Объемные поверхностные диаграммы отображают и соединительные линии и полигоны поверхности в цвете. Эта таблица приводит различные формы.
Используемый, чтобы создать
Объемная поверхностная диаграмма
Объемная поверхностная диаграмма с контурным графиком ниже его
Объемная поверхностная диаграмма с графиком занавеса (базовая плоскость)
График плоской поверхности (значение пропорционально только, чтобы окрасить),
Объемная поверхностная диаграмма освещается от заданного направления
Низкоуровневая функция (на котором высокоуровневые функции базируются) для создания поверхностных графических объектов
Функции для Gridding и Interpolating Data
Эти функции полезны, когда необходимо реструктурировать и интерполировать данные так, чтобы можно было представлять эти данные как поверхность.
Используемый, чтобы создать
Прямоугольная сетка в 2D и трехмерном пространстве
Интерполируйте данные, имеющий разброс
Interpolant для данных с координатной сеткой
Интерполируйте данные, имеющий разброс
Сетчатые графики и объемные поверхностные диаграммы
mesh и surf команды создают 3-D объемные поверхностные диаграммы матричных данных. Если Z матрица для который элементы Z(i,j) задайте высоту поверхности по базовому (i,j) сетка, затем
генерирует цветное, каркасное представление поверхности и отображает его в 3-D представлении. Точно так же
генерирует цветное, фасетное представление поверхности и отображает его в 3-D представлении. Обычно, фасеты являются четырехугольниками, каждый из которых является постоянным цветом, обрисованным в общих чертах с черными линиями mesh, но shading команда позволяет вам устранять линии mesh ( shading flat ) или выбрать интерполированную штриховку через фасет ( shading interp ).
Свойства объекта подложки обеспечивают дополнительное управление общим видом поверхности. Можно задать стили линии ребра, маркеры вершины, окраску поверхности, подсветку характеристик, и так далее.
Функции визуализации двух переменных
Отобразить функцию двух переменных, z = f ( x,y ), сгенерируйте X и Y матрицы, состоящие из повторных строк и столбцов, соответственно, по области функции. Вы будете использовать эти матрицы, чтобы оценить и изобразить функцию в виде графика.
Матричный R содержит расстояние от центра матрицы, которая является источником. Добавление eps предотвращает деление нулем (на следующем шаге), который производит Inf значения в данных.
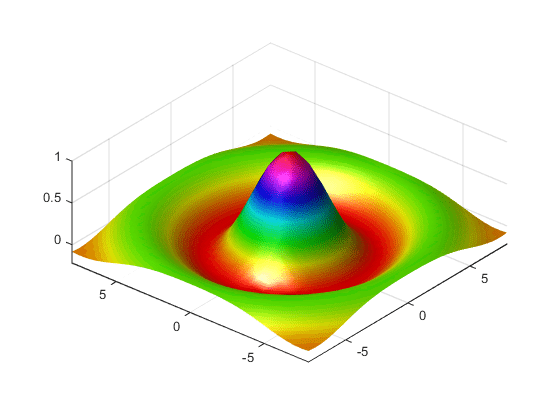
Формирование sinc функция и графический вывод Z с mesh результаты на 3-D поверхности.
Удаление невидимой линии
По умолчанию MATLAB удаляет линии, которые скрыты от представления в сетчатых графиках, даже при том, что поверхности графика не заполнены. Можно отключить удаление невидимой линии и позволить поверхностям сетчатого графика быть прозрачными с hidden команда:
Подчеркивание поверхностной формы
Смотрите surf функция для получения дополнительной информации об объемных поверхностных диаграммах.
Объемные поверхностные диаграммы неоднородно выборочных данных
Можно использовать meshgrid создать сетку однородно выборочных данных указывает, в котором можно оценить и изобразить в виде графика sinc функция. MATLAB затем создает объемную поверхностную диаграмму путем соединения соседних элементов матрицы, чтобы сформировать сетку четырехугольников.
Чтобы произвести объемную поверхностную диаграмму из неоднородно выборочных данных, используйте scatteredInterpolant интерполировать значения в однородно расположенных с интервалами точках, и затем использовать mesh и surf обычным способом.
Пример – отображение неоднородных данных по поверхности
Этот пример оценивает sinc функционируйте наугад указывает в определенной области значений и затем генерирует однородно выборочные данные для отображения как объемная поверхностная диаграмма. Процесс включает эти задачи:
Использование linspace сгенерировать равномерно распределенные значения в области значений ваших неравномерно выборочных данных.
Используйте функцию построения графика, чтобы отобразить данные.
Сгенерируйте неравномерно выборочные данные в области значений [-8, 8] и используйте ее, чтобы выполнить функцию:
linspace функция обеспечивает удобный способ создать однородно распределенные данные с желаемым числом элементов. Следующие операторы производят векторы в области значений случайных данных с тем же разрешением как сгенерированный-8:.5:8 оператором в предыдущем sinc пример:
Теперь используйте эти точки, чтобы сгенерировать однородно расположенную с интервалами сетку:
Ключ к этому процессу должен использовать scatteredInterpolant интерполировать значения функции в однородно расположенных с интервалами точках, на основе значений функции в исходных точках данных (которые случайны в этом примере). Этот оператор использует линейную интерполяцию по умолчанию, чтобы сгенерировать новые данные:
Постройте интерполированный и неоднородные данные, чтобы произвести:
Изменение данных
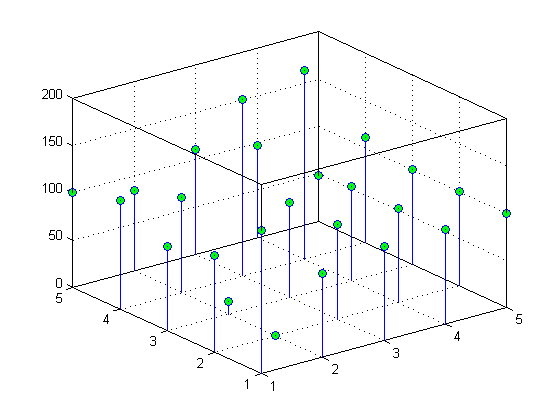
Предположим, что у вас есть набор данных со следующим (X, Y, Z) триплеты:
| X | Y | Z |
|---|---|---|
| 1 | 1 | 152 |
| 2 | 1 | 89 |
| 3 | 1 | 100 |
| 4 | 1 | 100 |
| 5 | 1 | 100 |
| 1 | 2 | 103 |
| 2 | 2 | 0 |
| 3 | 2 | 100 |
| 4 | 2 | 100 |
| 5 | 2 | 100 |
| 1 | 3 | 89 |
| 2 | 3 | 13 |
| 3 | 3 | 100 |
| 4 | 3 | 100 |
| 5 | 3 | 100 |
| 1 | 4 | 115 |
| 2 | 4 | 100 |
| 3 | 4 | 187 |
| 4 | 4 | 200 |
| 5 | 4 | 111 |
| 1 | 5 | 100 |
| 2 | 5 | 85 |
| 3 | 5 | 111 |
| 4 | 5 | 97 |
| 5 | 5 | 48 |
Изменение результатов в трех массивах 5 на 5:
Можно теперь представлять значения Z относительно X и Y. Например, создайте 3-D график основы:
Параметрические поверхности
описывает поверхность mesh с вершинами, имеющими цветной C(i,j) и расположенный в точках
где x соответствует столбцам Z и y к его строкам.
описывает поверхность mesh с вершинами, имеющими цветной C(i,j) и расположенный в точках
Документация
Примитивная объемная поверхностная диаграмма
Синтаксис
Описание
В отличие от этого, surf функция, примитив surface функция не вызывает newplot прежде, чем построить и не уважает значение NextPlot свойство для фигуры или осей. Вместо этого это добавляет объемную поверхностную диаграмму в текущую систему координат, не удаляя другие графические объекты или сбрасывая свойства осей.
Примеры
Создание объемной поверхностной диаграммы
Создайте три матрицы, одного размера. Затем постройте их как поверхность. Поверхность использует Z и для высоты и для цвета.
По умолчанию появитесь отображения в осях с помощью двумерного представления. Измените оси в 3D представление.
Определение цветов палитры для объемной поверхностной диаграммы
Изменение внешнего вида объемной поверхностной диаграммы
Используйте s получить доступ и изменить свойства объекта подложки после того, как это создается. Например, скройте ребра путем установки EdgeColor свойство.
Изображение на дисплее вдоль объемной поверхностной диаграммы
Создайте поверхность и отобразите изображение вдоль него.
Создайте три матрицы, одного размера.
Входные параметры
Можно использовать meshgrid функция, чтобы создать X и Y матрицы.
Пример: X = 1:10
Пример: X = [1 2 3; 1 2 3; 1 2 3]
Пример: [X,Y] = meshgrid(-5:0.5:5)
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Можно использовать meshgrid функция, чтобы создать X и Y матрицы.
Пример: Y = 1:10
Пример: Y = [1 1 1; 2 2 2; 3 3 3]
Пример: [X,Y] = meshgrid(-5:0.5:5)
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
z- в виде матрицы. Z должен иметь по крайней мере две строки и два столбца.
Z задает высоту объемной поверхностной диаграммы в каждом x— y координата. Если вы не задаете цвета, то Z также задает поверхностные цвета.
Пример: Z = [1 2 3; 4 5 6]
Пример: Z = sin(x) + cos(y)
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Чтобы использовать цвета палитры, задайте C как матрица. Для каждого узла решетки на поверхности, C указывает на цвет в палитре. CDataMapping свойство объекта подложки управляет как значения в C соответствуйте раскрашивает палитру.
Чтобы использовать цвета истинного цвета, задайте C как массив триплетов RGB.
Для получения дополнительной информации смотрите Различия Между Палитрами и Истинным цветом.
CData свойство объекта подложки хранит цветовую гамму. Для дополнительного управления окраской поверхности используйте FaceColor и EdgeColor свойства.
ax — Оси, чтобы построить в
объект осей
Оси, чтобы построить в в виде axes объект. Если вы не задаете оси, то surface графики в текущую систему координат.
Аргументы name-value
Пример: surface(X,Y,Z,’FaceAlpha’,0.5,’EdgeColor’,’none’) создает полупрозрачную поверхность без чертивших ребер.
Примечание
Цвет линии ребра в виде одного из значений, перечисленных здесь. Цвет по умолчанию [0 0 0] соответствует черным ребрам.
Используйте заданный цвет для всех ребер. Эта опция не использует значения цвета в CData свойство.
Триплеты RGB и шестнадцатеричные цветовые коды полезны для определения пользовательских цветов.
Кроме того, вы можете задать имена некоторых простых цветов. Эта таблица приводит опции именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Название цвета | Краткое название | Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ‘red’ | ‘r’ | [1 0 0] | ‘#FF0000’ |
| Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|
| [0 0.4470 0.7410] | ‘#0072BD’ | |
| ‘none’ | Никакая линия | Никакая линия |
Цвет поверхности в виде одного из значений в этой таблице.
Используйте заданный цвет для всех поверхностей. Эта опция не использует значения цвета в CData свойство.
Триплеты RGB и шестнадцатеричные цветовые коды полезны для определения пользовательских цветов.
Кроме того, вы можете задать имена некоторых простых цветов. Эта таблица приводит опции именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.