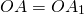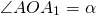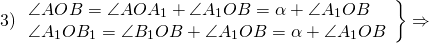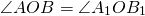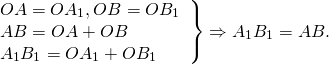Как сделать поворот в геометрии

Поворот

Отметим на плоскости точку O — центр поворота. Зададим угол α — угол поворота.

Поворот плоскости вокруг точки O на угол α — это отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, что

При этом точка O остаётся на месте (отображается сама в себя), а все остальные точки поворачиваются вокруг точки O в одном и том же направлении — либо по часовой стрелке, либо против часовой стрелки.

Поворот является движением

(то есть отображением плоскости на себя, сохраняющим расстояние).

Если точки A, O и B не лежат на одной прямой.

Пусть точка O — центр поворота, α — угол поворота. При повороте вокруг точки O на угол α против часовой стрелки точка A отобразится в точку A1, точка B — в точку B1.

Проведём отрезки AB и A1B1.

Рассмотрим треугольники AOB и A1OB1.

2) OB=OB1 (по определению поворота).

Следовательно, треугольники AOB и A1OB1 равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1.

Если точки A, O и B лежат на одной прямой.

При повороте в направлении по часовой стрелке все рассуждения аналогичны.

Равенство A1B1=AB означает, что при повороте расстояние между точками сохраняется, а значит, поворот является движением.

Источник

Параллельный перенос и поворот

Вы будете перенаправлены на Автор24

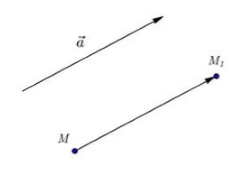
Параллельный перенос

Рисунок 1. Параллельный перенос

Введем следующую теорему.

Параллельный перенос является движением.

Доказательство.

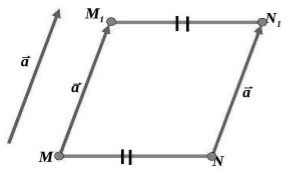
Рисунок 2. Иллюстрация теоремы 1

Теорема доказана.

Поворот

Готовые работы на аналогичную тему

Введем следующую теорему.

Поворот является движением.

Доказательство.

Рисунок 4. Иллюстрация теоремы 2

Теорема доказана.

Примеры задач на параллельный перенос и поворот

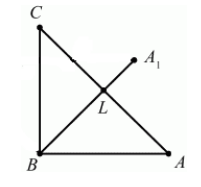
Решение.

\[\angle CBC_1=<45>^0,\ \ BC=BC_1\]

Решение закончено.

Решение.

Решение закончено.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15 04 2021

Источник

Что такое движения плоскости: параллельный перенос, поворот. Преобразование подобия. Гомотетия

Если каждой точке плоскости ставится в соответствие некоторая точка из этой же плоскости, и если при этом любая точка плоскости оказывается сопоставленной определенной точке, то говорят, что это отображение плоскости на себя. Любое отображение плоскости на себя, при котором остаются неизменными расстояния между точками, называют движением плоскости.

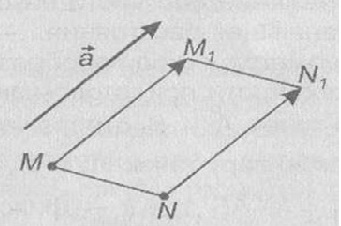
Параллельный перенос. Пусть а — данный вектор. Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в точку М₁, что вектор MМ₁ равен вектору а.

Параллельный перенос является движением, поскольку представляет собой отображение плоскости на себя, сохраняющее расстояния. Наглядно это движение можно представить как сдвиг всей плоскости в направлении данного вектора а на его длину.

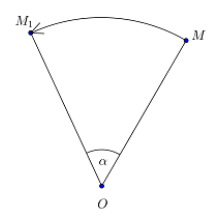
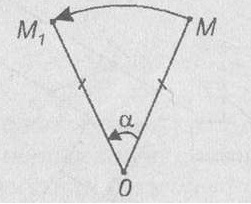
Поворот. Обозначим на плоскости точку О (центр поворота) и зададим угол α (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в точку М₁, что ОМ = ОМ₁ и угол MOМ₁ равен α. При этом точка О остается на своем месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одинаковом направлении — по часовой стрелке или против часовой стрелки (на рисунке изображен поворот против часовой стрелки).

Поворот является движением, поскольку представляет собой отображение плоскости на себя, при котором сохраняются расстояния.

Геометрическое преобразование плоскости, при котором любая пара точек А и В отображается на такую пару точек А₁ и В₁, что А₁ В₁ = k∙АВ, где k — фиксированная для данного преобразования положительная константа, называется преобразованием подобия. Число k называется при этом коэффициентом подобия.

Очевидно, что движения плоскости — частный случай подобия (с коэффициентом 1).

Свойства преобразования подобия.

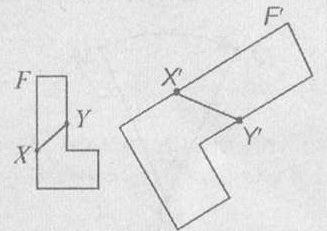
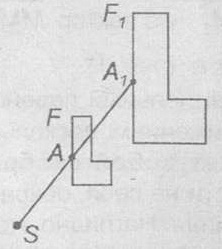
Геометрическое преобразование плоскости с неподвижной точкой S, которое всякой точке А, отличной от S, ставит в соответствие такую точку А₁, что SА₁ = k∙SA, где k ≠ 0 — наперед заданное число, называется гомотетией с центром S и коэффициентом k. Если фигура F₁ получена из фигуры F с помощью гомотетии, то фигуры F и F₁ называются гомотетичными.

Свойства гомотетии.

Источник

Геометрия. 9 класс

Отметим на плоскости точку О – центр поворота и зададим угол α – угол поворота. Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁ и угол МОМ₁ равен α. Этот вид отображения плоскости на себя называется поворотом.
Задачи на построение:
Задача 1. Построим поворот точки М на угол в 600 по часовой стрелке вокруг точки О.
1. Отметим точки О и М.
2. Проведем луч ОМ.
3. Отложим с помощью транспортира угол в 600.
4. На проведенном луче циркулем отложим отрезок, равный ОМ.
5. Поставим точку М₁.

При этом точка М отображается в точку М₁.
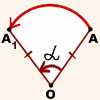
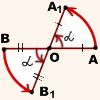
Задача 2. Построим отрезок, в который переходит отрезок АВ при повороте на 120° против часовой стрелки около точки О.

1. Проведем луч ОА.
2. От него против часовой стрелки отложим ∠АОА₁ = 120°.
3. ОА = ОА₁;
4. Проведем луч ОВ.
5. От него против часовой стрелки отложим ∠ВОВ₁ = 120°.
6. ОВ = ОВ₁, А₁В₁ – образ отрезка АВ при повороте вокруг точки О на 120° против часовой стрелки.
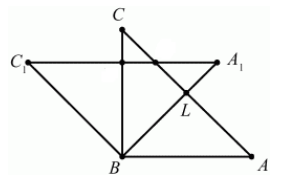
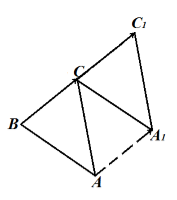
Задача 3. Построим треугольник ABC и зададим некоторый угол поворота α. Повернем каждую из точек А, В, С на угол α против часовой стрелки.

При этом точка А отображается в точку А₁, точка отображается в точку В₁, точка С отображается в точку С₁.
Соединим отрезками точки А₁, В₁, С₁. Треугольник АВС отображается на треугольник А₁В₁С₁ при повороте на угол α.
Выделение существенных признаков поворота.
1. Отображение плоскости на себя.
2. Каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁
3. ∠МОМ₁ = α.
Сравним данную фигуру и её отображение. Что общего в них?
Является ли поворот движением – отображением плоскости на себя, сохраняющим расстояние?
Доказательство: пусть при повороте на угол α точки А и В отображаются в точки А₁ и В₁.Треугольники ОАВ и ОА₁В₁ равны по двум сторонам и углу между ними: ОА = ОА₁, ОВ = ОВ₁ и ∠АОВ = ∠А₁ОВ₁ значит АВ = А₁В₁. Т.е расстояние между точками А и В равно расстоянию между точками А₁ и В₁.
Отметим следующие свойства.
При повороте
1) отрезок переходит в равный ему отрезок;
2) угол переходит в равный ему угол;
3) окружность переходит в равную ей окружность;
4) любой многоугольник переходит в равный ему многоугольник;
5) параллельные прямые переходят в параллельные прямые;
6) перпендикулярные прямые переходят в перпендикулярные прямые.
Чтобы задать поворот достаточно задать центр поворота, угол поворота, направление поворота.
Поворот на 180° по часовой стрелке совпадает с поворотом этой же точки на 180° против часовой стрелки и является центральной симметрией.

Источник

Поворот

Отметим на плоскости точку О (центр поворота) и зададим угол а (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁ и угол МОМ₁ равен α (рис. 330). При этом точка О остаётся на месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении — по часовой стрелке или против часовой стрелки. На рисунке 330 изображён поворот против часовой стрелки.

Поворот является движением, т. е. отображением плоскости на себя, сохраняющим расстояния.

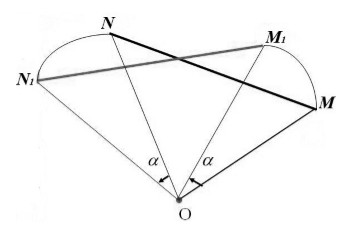
Докажем это. Пусть О — центр поворота, α — угол поворота против часовой стрелки (случай поворота по часовой стрелке рассматривается аналогично). Допустим, что при этом повороте точки М и N отображаются в точки М₁ и N₁ (рис. 331). Треугольники OMN и ОМ₁N₁ равны по двум сторонам и углу между ними: ОМ = ОМ₁, ON = ON₁ и ∠MON = ∠M₁ON₁ (для случая, изображённого на рисунке 331, каждый из этих углов равен сумме угла α и угла M₁ON). Из равенства этих треугольников следует, что MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М, и N, (случай, когда точки О, М и N расположены на одной прямой, рассмотрите самостоятельно). Итак, поворот сохраняет расстояния между точками и поэтому представляет собой движение. Это движение можно представить себе как поворот всей плоскости вокруг данной точки О на данный угол α.

Источник