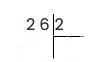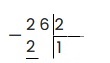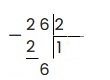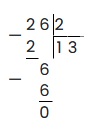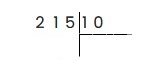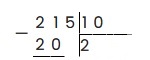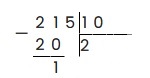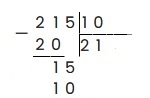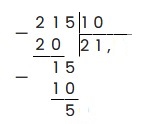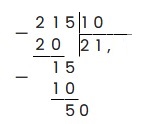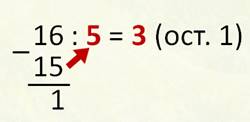Как сделать проверку деления столбиком
Деление в столбик
Сегодня мы рассмотрим вопрос, касающийся деления в столбик. Познакомимся с алгоритмом и закрепим материал на конкретных примерах.
Алгоритм деления в столбик
Делить столбиком гораздо проще, чем считать в уме. Для этого необходимо воспользоваться простым алгоритмом:
Примеры
Рассмотрим несколько примеров на закрепление алгоритма деления в столбик.
Пример 1: Разделить 26 на 2.
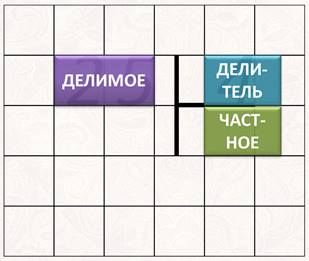
Слева записываем делимое, справа делитель, рисуем уголок.
Делимое у нас — 26, делитель — 2. Наименьшее число, которое можно взять из делимого и разделить на 2, будет двойка. 2 делим на 2, получаем 1. 2 умножить на 1 получится 2. Записываем это:
2 — 2 = 0, ноль писать не обязательно, поэтому исходя из алгоритма скидываем следующую цифру из делимого — 6
6 делим на 2 получаем 3, записываем в частное. 3 умножаем на 2 получаем 6. 6 — 6 = 0
Пример 2: Разделить 215 на 10.
Аналогично предыдущему примеру записываем условие уголком:
Наименьшее число, которое можно выделить из 215 и разделить на 10 — это 21. 21 делим на 10, и записываем в частное целую часть — 2. 2 умножаем на 10 — получаем 20:
21 — 20 = 1, записываем в остаток:
Сбрасываем из делимого оставшуюся цифру — 5, получаем 15. Аналогично делим 15 на 10 и получаем целую часть 1. 1 умножаем на 10, получаем 10, записываем:
15 — 10 = 5, записываем в остаток. 5 нацело на 10 не делится. Возвращаемся к 7 пункту алгоритма и ставим запятую в частном:
А, к остатку добавляем 0:
Теперь 50 мы легко можем разделить на 10 без остатка:
Деление в столбик
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.
Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза.
Проверяем: 4 × 7 = 28, а 28
Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся двойку и продолжаем размышлять.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Как выглядит деление в столбик с остатком
Это такое же деление, только в результате получается неровное число, как получилось в примере выше.
Примеры на деление в столбик
Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!
Деление в столбик.
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида 
Например, если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.
Как делить в столбик лучше всего объяснить на примере. Вычислить :
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2) ).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое «промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Значит, 1976 : 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Десятичные дроби онлайн. Перевод десятичных дробей в обычные и обычных дробей в десятичные.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить поразрядное деление и получить в частном десятичную дробь.
Например, 64 разделим на 5.
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего, меньшего разряда и продолжать деление.
Деление с остатком столбиком. Проверка деления с остатком
Урок 36. Математика 3 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Деление с остатком столбиком. Проверка деления с остатком»
Привет, друзья! А вот и я.
Опять буду знакомить вас с новой темой. Я надеюсь, вы уже уверенно научились выполнять деление с остатком? Помните, как мы шестнадцать делили на пять?
Вспоминаем таблицу умножения и деления с числом пять. Находим число, которое делится на пять без остатка и на числовом луче находится ближе остальных к числу шестнадцать. Это пятнадцать. Пятнадцать делим на пять, получается три, а разницу между шестнадцатью и пятнадцатью – один, записываем в остаток.
Вы уже знаете, что знак умножения может записываться по-разному – иногда точкой, иногда косым крестиком, а на клавиатуре компьютера или мобильного телефона – звёздочкой. Но и знак деления тоже может выглядеть по-разному: в тетрадях вы обычно пишете двоеточие, иногда этот знак выглядит как горизонтальная черта, а над ней и под ней по точке. Но для письменного деления многозначных чисел используют знак деления, который похож на лежащую на боку букву Т. И сегодня мы воспользуемся таким знаком деления для того, чтобы выполнять деление с остатком столбиком.
Вот посмотрите, допустим, нам надо разделить число двадцать пять на четыре.
Как это записать, я покажу на разлиновке в клеточку. Ведь при таком способе решения, как и при сложении и вычитании столбиком, очень важна аккуратность записи. Итак, пишу делимое – число двадцать пять. Справа от него, отступив одну клеточку, пишу делитель – четыре. Между ними ставлю знак деления – вертикальная черта длиной в две клетки, а от неё – горизонтальная. Вот она, буква Т. Вот делимое, вот делитель. Под чертой место для частного.
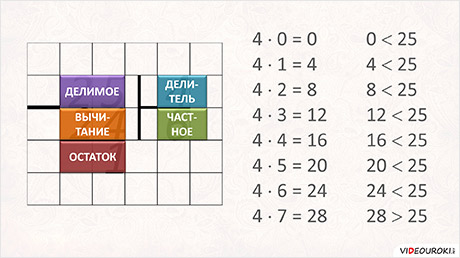
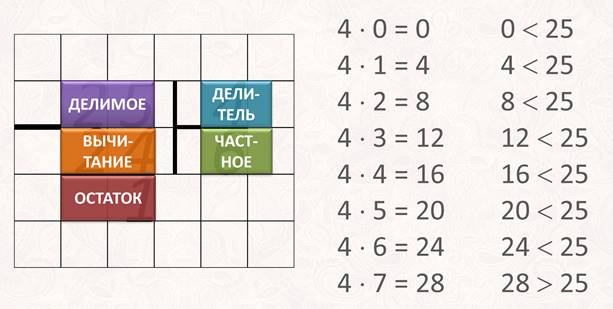
Сначала выясним, сколько раз число четыре содержится в двадцати пяти. Четыре умножаем на нуль, равно нуль. Нуль меньше двадцати пяти. Так что нуль в качестве частного нам уж точно не подходит.
Четыре умножаю на один. Четыре. Это число тоже меньше двадцати пяти и тоже нас не устраивает. Четыре умножаю на два – шесть. Оно тоже меньше двадцати пяти. Четыре умножаю на три – двенадцать, четырежды четыре – шестнадцать, четырежды пять – двадцать. Четыре умножить на шесть – двадцать четыре. На семь – двадцать восемь. А двадцать восемь не меньше, а больше двадцати пяти.
Стоп! Теперь получилось число, которое больше нашего делимого. Но это недопустимо. Возвращаемся к шестёрке. Итак, четыре содержится в числе двадцать пять шесть раз. Записываю в частном число шесть. А под делимым – то число, которое получилось при умножении делителя и частного – двадцать четыре.
А теперь вычитаю из делимого это полученное число двадцать четыре. Видите, получилось вычитание столбиком. А результат вычитания – это остаток. Я надеюсь, вы не забыли, что остаток обязательно должен быть меньше делителя. В этом примере остаток один. Он меньше четырёх. Значит, деление выполнено верно.
Запомните, как расположены компоненты деления. Делимое и делитель находятся на одной строчке, между ними пропускается одна клеточка. Частное расположено под делителем, а под делимым – действие вычитания и остаток.
Конечно, у нас получилось очень длинное вычисление. Методом проб и ошибок, начиная с нуля, мы нашли нужное нам число. Но, если вы хорошо знаете таблицу умножения, подбор нужного числа не будет столь долгим и утомительным.
Вот, к примеру, надо сорок пять разделить на шесть. Вспомнив таблицу умножения числа шесть, мы можем сказать, что ближайшими числами к делимому, которые делятся на шесть, являются числа сорок два и сорок восемь. Сорок восемь получится в результате умножения шести на восемь. Но число сорок восемь больше сорока пяти, и оно нам не подойдёт.
Сорок два получится в результате умножения шести на семь. Сорок два меньше сорока пяти. Значит, шесть содержится в сорока пяти семь раз. А остаток три. Наш остаток меньше делителя, значит, деление выполнено верно.
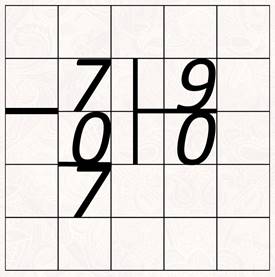
Ну а если, к примеру, надо число семь разделить на девять. Сколько раз число девять содержится в семи? Ну конечно, нуль раз. В частном записываем нуль. Нуль умножили на девять, тоже получился нуль, вычитаем. Остаток семь.
Если делимое меньше делителя, то в ответе получится нуль, а остаток будет равен делимому.
Ребята, а вы знаете, несмотря на то, что вы вроде бы всё правильно делаете, при делении с остатком случаются и ошибки. Как же проверить, правильно ли было выполнено деление?
Ну конечно обратными действиями. Мы выполняли деление и, чтобы найти остаток, вычитание. Значит, для проверки нам понадобится умножение и сложение.
Давайте сейчас разделим число сорок три на одиннадцать. Запишем решение в строчку. Сколько раз одиннадцать содержится в числе сорок три? Ну понятно, что не нуль и не один раз. Если взять два, получится число двадцать два. Оно меньше сорока трёх. Если взять три раза – это тридцать три. Оно тоже меньше сорока трёх. Возьмём число четыре – получится сорок четыре. Оно больше сорока трёх. Стоп! Возвращаемся к числу три. Число одиннадцать содержится в сорока трёх три раза и остаток десять.
Вроде бы всё правильно. Но убедиться в этом мы сможем, только выполнив проверку. Сравниваем остаток с делителем. Десять меньше одиннадцати. Это правильно. Теперь деление и вычитание проверяем умножением и сложением.
Делитель, одиннадцать, умножаем на частное, три, и к результату прибавляем остаток, десять. Одиннадцать умножить на три – тридцать три, и плюс десять – сорок три.
Ну, вроде бы всё рассказал. Ну, а если что-то по рассеянности пропустил, вам обязательно расскажет это ваш мудрый учитель.
А теперь я предлагаю вам повторить то, о чём мы сегодня говорили.
* Деление с остатком можно записывать как в строчку, так и столбиком.
* При записи столбиком делимое и делитель находятся на одной строчке, между ними пропускается одна клеточка, в которой записывается знак деления, похожий на букву Т, лежащую на боку. Частное расположено под делителем, а под делимым – действие вычитания и остаток.
Если делимое меньше делителя, то в ответе получится нуль, а остаток будет равен делимому.
Деление с остатком можно проверить.
1. Для этого сначала сравниваются остаток с делителем.
Важно! Остаток должен быть меньше делителя!
После сравнения остатка с делителем выполняем второй этап проверки.
2. Умножить частное на делитель и к полученному произведению прибавить остаток.
Ну вот и пришло время нам сегодня попрощаться. Хороших вам отметок, ребята! До свидания!
разделить столбиком
Как разделить столбиком, правило деления столбиком, примеры как делить делить два числа столбиком, онлайн деление столбиком. Разделить любое число на любое онлайн в столбик.
О делении двух чисел столбиком.
Правило деления столбиком
Правило деления в столбик звучит так :
Алгоритм деления столбиком пошагово!
Если вы еще не изучали десятичные дроби. То здесь мы останавливаемся.
Результат деления двух чисел столбиком :
При делении двух чисел 23 на 4 получили результат : неполное частное(или целое) равно 5.
Но и 3 далее можно было продолжить делить, но мы бы перешли в зону десятичных. См. пример деления с десятичными.
Как называются числа при делении столбиком!?
При делении столбиком, чтобы оперировать к каждому участнику данного математического действия у него есть собственное название:
Формула деления числа столбиком
Как таковой формулы деления столбиком не существует, есть несколько правил деления столбиком. И которые рассматривать отдельно, гипотетически глупо! Если вы никогда не делили столбиком, то вы никогда этого не поймете!
Поэтому. для понимания деления столбиком надо рассмотреть пример деления столбиком:
Как называются числа при делении в строке
Кроме названий чисел при делении столбиком, у нас есть еще запись деления в строку.
И там названий чуть поменьше.
Как называются числа при делении
Числа при делении называются так :
Первое число при делении называется «делимое«.
Второе число при делении называется «делитель«.
Третье число при делении называется «частное«.
Как запомнить «как называются числа при делении».
Есть огромное количество способов запомнить «как называются числа при делении«, вы их можете найти в интернете.
У меня есть свой способ.
Пример деления столбиком
Предположим, что нам нужно разделить число 102 на 4
Разберем это на картинке :
От 10 отняли 8 и ставим его под черту под цифру 8 и если это число получилось меньше 4, то значит нод был найден верно! И нодом нам придется пользоваться много раз, поэтому нужно научиться его находить!
Теперь, у нас в самом верху еще осталась одна двойка, её сносим ниже к двойке, которая получилась отниманием от 10 восьмерки, получается число 22.
5 заносим его под черту, ставим его после первого найденого нода.
Сносим наш ноль до остатка, что получается 20.
Заносим 5 под черту рядом с запятой.
Умножаем 4 на 5 = 20.
Ставим его под нашим остатком и нулем.
Итого результат деления столбиком:
Если разделить 102 на 4 столбиком, то мы получим 25.5, как впрочем и на калькуляторе, будет тоже самое.
Деление столбиком с остатком
Если мы разберем выше приведенный пример, то если мы возьмем картинку до добавления нуля, когда мы создали число 1020, то и полуим деление числа с остатком, остаток в данном случае равен двум:
Деление столбиком без остатка
Деление столбиком если делимое меньше делителя
Как разделить столбиком, если делитель больше делимого!
Предположим, что вам нужно разделить 4 на 5.
Располагаем стандартно наши числа слева делимое, справа делитель.
Ясно, что делитель больше делимого 5 > 4.
Поэтому, рядом с число 4 пишем ноль(выделено зеленым) и одновременно, этот же ноль записываем под делителем и добавляем точку.
Разберем второй пример :
Предположим, что нам нужно разделить 4 на 50.
Располагаем стандарно, наши числа для деления столбиком.
Ясно, что 4 меньше 50.
Пишем ноль рядом с 4, и одновременно ноль пишем под чертой ставим точку.
Далее аналогичные действия, что производили в первом варианте.
Зачем для примера были выбраны такие простые примеры!?
Числа выбраны простые намеренно, чтобы вам было понятно, как происходит деление, когда делитель больше делимого!