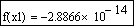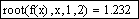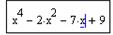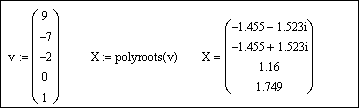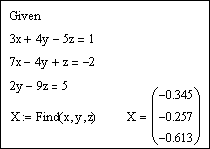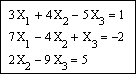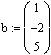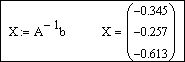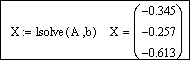Как сделать проверку в маткаде

Решение систем уравнений в MathCad

Для решения уравнений в Mathcad можно воспользоваться двумя способами. Эти способы были частично рассмотрены в разделе «Решение уравнений»:

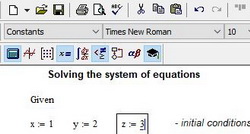
В рабочем поле mathcad записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения системы уравнений численными методами.

Затем указывается начальное приближение для искомых переменных. Это нужно для увеличения скорости и точности решения системы. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю для всех переменных, при этом, если окажется, что система имеет несколько решений, то есть риск не определить все корни. Поэтому лучше всегда задавать приближение

Рис. 1. Ввод исходных данных в поле mathcad

Далее вводятся уравнения. Их можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)

Рис. 2. Панели Boolean и Calculator

Рис. 3. Ввод функции Find()

Для того чтобы увидеть результат решения системы уравнений, после Find(x, y, z. ) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 4).

Рис. 4. Панель «Evaluation»

В зависимости от сложности системы через определенное время MathCad выведет результат. На рис. 5 можно рассмотреть синтаксис и результат решения системы уравнений. Обратите внимание, что можно присваивать результат решения системы матричной переменной и можно работать с отдельными ее элементами

Рис. 5. Результат численного решения системы уравнений

Mathcad позволяет решать системы уравний в символьном виде. Обычно это полезно, когда требуется получить не точное значение переменных, а их выражения через константы. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, y и z, то результат выведется в символьном виде (см. рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот метод

Рис. 6. Результат символьного решения системы уравнений

Использование метода Solve:

Как показывает практика, методом solve иногда удается решить системы уравнений, которые не поддаются решению с помощью функции Find()

Синтаксис следующий: на панели matrix нажимаем иконку Matrix or Vector и в появившемся окне указываем количество уравнений входящих в систему. В нашем примере их будет три (см. рис. 7)

Рис. 7. Создание матрицы для метода SOLVE

Заполняем систему, вводя последовательно все уравнения используя логический символ «ровно» из панели Boolean. Каждый элемент матрицы-столбца содержит одно уравнение (см. рис. 8)

Рис. 8. Ввод системы уравнений для метода SOLVE

Когда все уравнения введены, убедитесь, что курсор ввода находится в вашей матрице и затем нажмите кнопку «solve» из панели Symbolic. Появится служебное слово (функция) solve. Далее поставте запятую и введите последовательно все переменные, относительно которых необходимо решить систему уравнений (см. рис. 9)

Рис. 9. Синтаксис метода SOLVE для решения систем

Уведите курсор в свободное поле mathcad и дождитесь окончания решения системы. Обратите внимание, что мы не вводили начальные приближения. Даный метод их назначает автоматически. Обратите так же внимание, что для решения системы в символьном виде синтаксис аналогичен (см. рис. 10)

Рис. 10. Синтаксис метода SOLVE для решения систем

Как показывает моя инженерная практика, решение систем в символьном виде сопряжено с большими вычислительными трудностями. То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Источник

Как сделать проверку в маткаде

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

Этот прием используется в Mathcad так:

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

Задание 1. Решить уравнение .

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

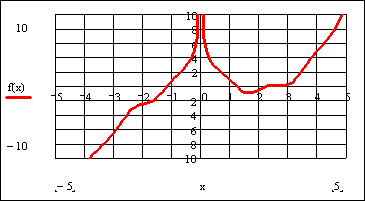
После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .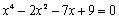

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений 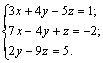Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

Источник

Урок 15. Проверка данных в Mathcad

Есть данные о двух процедурах лечения пациентов:

Нужно использовать эти данные, чтобы определить какая из этих процедур играет большую роль. Можно ли сказать, что процедура A лучше, чем процедура B? У процедуры A выше средний показатель и лучше воспроизводимость, чем в методике B? Сложность заключается в том, что в данных присутствуют статистические флуктуации, и нельзя быть уверенным в найденных значениях. Проверки статистических данных помогут решить этот вопрос. Сначала обратим внимание на поведение выборок.

Поведение выборок

График ниже показывает распределение генеральной совокупности со средним X_ и среднеквадратическим отклонением S. Обычно мы не знаем этих значений, мы можем лишь оценить их по значениям среднего x_ и СКО s выборке. Если выборка достаточно большая и репрезентативная, можно ожидать, что:

Вопрос состоит в том, насколько большую разницу между X_ и x_ можно ожидать. Чтобы определить ее, нужно посмотреть на распределение средних значений большого числа выборок. Это нормальное распределение с математическим ожиданием и дисперсией:

Последнее равенство приблизительное. Дисперсия S’ называется ошибкой выборки. Чем больше размер выборки n, тем меньше ошибка.

Распределение выборки будет сходно с распределением генеральной совокупности, но не точно таким же. Средние значения выборок будут иметь более узкие распределения, их среднее X’_ должно быть таким же, как у генеральной совокупности.

Стандартное отклонение часто определяется экспериментально с помощью измерительного оборудования, и нужно иметь возможность включать данные из других выборок для получения более точной оценки.

Ожидается, что среднее значение генеральной совокупности должно быть расположено в интервале около среднего значения выборки:

Если z=2, среднее значение генеральной совокупности будет лежать внутри интервала в 95% случаев. Ширина этого доверительного интервала зависит от ? – доверительной вероятности.

Мы можем уменьшить этот интервал, уменьшая доверительную вероятность. Мы можем также уменьшить интервал, уменьшая ошибку выборки. Это можно сделать, увеличивая размер выборки или улучшая методику измерения для уменьшения s. Можно ожидать хороших доверительных оценок, если только данные удовлетворяют двум требованиям:

Первое требование достаточно трудно достижимо на практике, поэтому неопределенность в результате часто высока.

Выбор размера выборки

Чтобы определить, насколько большой должна быть выборка, мы предполагаем, что мы знаем среднее значение X_ и СКО генеральной совокупности. Мы хотим ограничить ошибку выборки значением:

Если СКО генеральной совокупности уже меньше, чем желаемое значение ошибки выборки, то нужно лишь одно наблюдение:

В других случаях мы можем уменьшить ошибку выборки, проводя больше наблюдений:

Для примера возьмем:

Проведя 25 наблюдений, мы уменьшим ошибку выборки на 5. (Часто минимальное количество в выборке задается n=30.)

Заявка на патент

Каков доверительный интервал в выборках заявки на патент? Ошибки выборки равны:

Мы построили графики интервалов 95%. Они сильно перекрываются – разница не достаточно велика, чтобы одобрить патент…

Эта кривая погрешности использует в качестве легенды по осям x и y две матрицы:

Первая содержит две строковых переменных, вторая – границы интервалов.

Оценка при работе с категориями

Хотя уравнения для категорий схожи с уравнениями для чисел, два из них отличаются существенно.

Побочный эффект лекарства

Чтобы проиллюстрировать статистические расчеты при работе с категориями, мы посмотрим на побочный эффект лекарства. При испытаниях 26 из 374 пациентов (7%) чувствовали себя плохо, вместе с 4 из 410 (1%), которым давали плацебо:

Вопрос: это случайность, или необходимо заключить, что пациенты чувствуют себя плохо из-за лекарства?

Свойства выборок категорий

С данными категорий мы также обычно не знаем среднее значение вероятности и СКО генеральной совокупности, но мы можем оценить их по выборке. Параметры выборки:

СКО малой вероятности больше, чем сама вероятность. Это отличие от свойств чисел, где СКО обычно меньше в сравнении со средним. Ошибка выборки определяется также, как и для чисел:

Для уменьшения ошибки необходимо увеличивать число n. Относительная ошибка уменьшается в fраз:

Мы можем вывести уравнение для поиска необходимого числа наблюдений в выборке:

Например, если мы хотим уменьшить ошибку в 5 раз, мы находим для вероятности 0,1:

Если p близка к 0 или к 1, нужна большая выборка – часто это число достигает 1000. Мы ожидаем, что среднее значение вероятности генеральной совокупности лежит в интервале:

Для лекарства мы находим:

График погрешности показывает, что 95%-ные доверительные интервалы двух наборов данных не перекрываются – эти наборы данных совершенно различны. Значит, нужно заключить, что лекарство заставляет чувствовать себя плохо 10% больных.

Формальные проверки

Проверки можно провести более формально. Идея состоит в том, чтобы выявить, есть ли основания полагать, что есть разница между двумя наборами данных. В таблице ниже приведены уравнения для четырех тестов. Чтобы использовать уравнения для проверки, нужно заранее выбрать значение z.

Пример: заявка на патент

В примере с заявкой на патент мы приняли во внимание разницу между средними значениями двух выборок. Данные:

Это выражение истинно, поэтому мы не можем различить эти две выборки.

В примере с лекарством данные:

Выражение ложно, поэтому:

Выбор z

При формальном испытании решающее значение имеет выбор величины z. Она определяет, в какой точке утверждение меняется от ложного до истинного.

Доверительная вероятность 95% является хорошим компромиссом и часто используется в статистике. Однако, Вы не ограничены этим значением.

В зависимости от Вашей проблемы, Вы можете хотеть избежать различных участков распределения. Это зависит от того, какое значение z Вы выберите. Мы проиллюстрируем это на примере трех компонентов фармацевтического препарата. Красным выделены нежелаемые области.

Мы покажем расчет границ на рисунках выше, используя нормальное распределение и так называемое распределение Стьюдента. Распределение Стьюдента похоже на нормальное, но оно лучше для малых выборок. Используемые параметры:

Резюме

Последняя величина называется ошибкой выборки.

При z=2 можно ожидать, что 95% всех возможных средних значений выборок попадут в 95%-ный доверительный интервал:

Используемая ошибка выборки является комбинацией двух ошибок. Этот метод требует определения, какие значения z нужно включить, а какие исключить.

Источник