Как сделать тетраэдр в компасе

18.09.202218.09.2022 admin 0 Comments

Глава 11. Решения планиметрических задач с помощью двумерного редактора

Рис. 11.7. Определение периметра Р треугольника АВС с медианой AK = 20 мм, при:

а — АВ = 30 мм, BK = 16 мм; б — ВС = 35 мм, высоте АР = 15 мм;

2. Примеры по разным темам

Пример 11.8
Условие. Две окружности, диаметры которых равны 30 и 20 мм, имеют внут-
реннее касание в точке А (рис. 11.8, а). Найти диаметр третьей окружности,
касающейся двух и их общего диаметра.
Решение. Вначале необходимо построить две окружности заданных диа-
метров и отрезок, проходящий через их центры. Затем необходимо вызвать
команду Окружность, касательная к трем кривым, построить третью
окружность и измерить ее диаметр.

Пример 11.9
Условие. В прямоугольном треугольнике ABC, гипотенуза АВ которого равна
30 мм, проведены медианы АМ и ВN (рис. 11.8, б). Известно, около четырех-
угольника ABMN можно описать окружность. Найти ее диаметр.

Рис. 11.8. Построения и измерения: а — примера 11.8; б — примера 11.9

Решение. Вначале строится отрезок АВ заданной длины. Затем из точек А и В
проводятся два отрезка под углами 135° и 45° и с использованием команды

Источник

Разработка методических рекомендаций по созданию моделей гексаэдра, тетраэдра и октаэдра в программном комплексе Компас-3D V16

Студент первого курса факультета ПГС

(Новосибирск, Сибирский государственный университет путей сообщения (СГУПС))

Разработка методических рекомендаций по созданию моделей гексаэдра, тетраэдра и октаэдра в программном комплексе Компас-3D V16

Актуальность исследования. Правильные многогранники это поверхности с высокой степенью симметричности. Особенности их геометрии позволяют легко вычислять центры масс тел имеющих форму правильных многогранников и другие их геометрические параметры, вписывать один в другой или в сферу. Именно поэтому правильные многогранники широко используются в технике, архитектуре и строительстве.

Цель исследования – разработать методические рекомендации по моделированию гексаэдра, тетраэдра и октаэдра в программном комплексе Компас-3D V16.

Задача исследование – разработка методических рекомендаций по моделированию нескольких правильных многогранников с помощью стандартных инструментов Компас-3D.

Вначале исследования мы изучали свойства правильных многогранников для того чтобы выявить те их них которые позволят выбрать наиболее эффективные методы их моделирования. Затем было выполнено пилотное моделирование разными способами и выбран самый простой и быстрый их них, На втором этапе были разработаны методические рекомендации по решению задачи.

1. Методические рекомендации по созданию модели гексаэдра.

Рисунок 1. Модель гексаэдра.

2. Методические рекомендации по созданию модели тетраэдра.

Тетраэдр – это пирамида, у которой все грани являются правильными треугольниками. Число вершин у тетраэдра – четыре. В каждой вершине сходятся по три треугольных грани и три ребра. Тетраэдр может быть вписан в куб или в другой правильный многогранник. На этом свойстве основан выбранный нами способ его моделирования. Мы будем усекать куб диагональными плоскостями, проходящими через вершины куба, находящиеся на смежных гранях.

Рисунок 2. Модель правильного тетраэдра.

3. Методические рекомендации по созданию модели октаэдра.

Грани октаэдра являются правильными треугольниками. В каждой вершине сходится четыре грани. Всего их восемь.

Затем строим четыре вспомогательные плоскости так, чтобы каждая из них проходила через три точки, расположенные на ребрах, сходящихся в одной вершине.

Рисунок 3. Модель октаэдра.

Таким образом, мы построили три правильных многогранника, используя способ отсечения вершин.

Задача исследования решена. Цель достигнута. Разработаны и апробированы методические рекомендации по моделированию гексаэдра, тетраэдра и октаэдра в программном комплексе Компас-3D V16.

Разработанная проста в использовании и наглядна, и не требует большого опыта работы в Компас-3D, универсальна. Может быть полезна при выполнении курсовых заданий и расчетно-графических работ по стереометрии, начертательной геометрии и инженерной графике.

Источник

12.4. Моделирование правильных треугольных пирамид

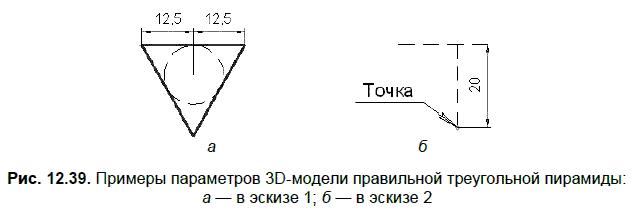
Если 3D-модель тетраэдра можно построить по одному параметру, например по длине ребра, то для создания модели правильной треугольной пирамиды требуются два параметра. В наиболее очевидном способе создания 3D-модели первый параметр определяет геометрию основания (равностороннего треугольника), второй параметр задает высоту пирамиды. При использовании пользовательской ориентации Изометрия XYZ и операции По сечениям для создания правильной треугольной пирамиды эскиз 1 в плоскости zx может иметь вид, показанный на рис. 12.39, а, а эскиз 2 (одна точка) в плоскости zy — вид, показанный на рис. 12.39, б.

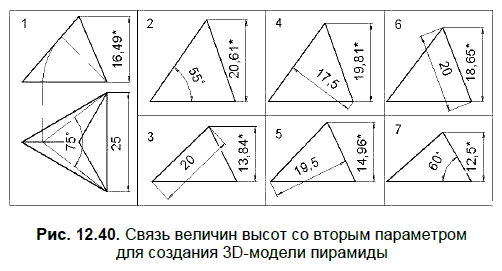
На рис. 12.40 представлены еще 7 способов создания 3D-модели правильной треугольной пирамиды, когда первый параметр — длина ребра основания, равная 25 мм, а вторым параметром является следующая величина:

1. Угол между боковыми гранями (75).

2. Угол между основанием и боковым ребром (55°).

3. Длина бокового ребра (20 мм).

4. Расстояние между скрещивающимися ребрами (17,5 мм).

5. Расстояние между боковой гранью и противолежащей вершиной (19,5 мм).

6. Высота боковой грани (20 мм).

7. Угол между основанием и боковой гранью (60°).

На рис. 12.40 со знаком «*» указан также зависимый параметр — высота пирамиды, построенной по двум заданным параметрам.

Величины высот, показанные на рис. 12.39, могут быть найдены в результате решения элементарных планиметрических задач, или в результате несложных построений с последующим измерением искомой величины.

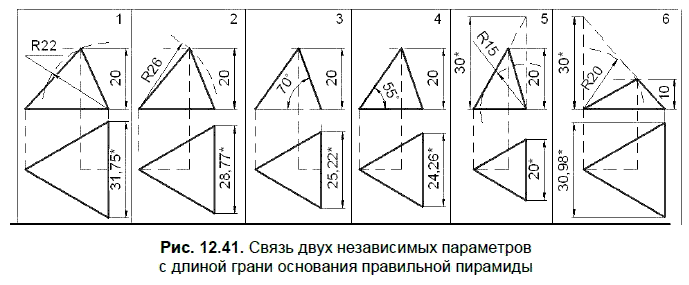
На рис. 12.41 представлены 6 способов создания 3D-модели правильной треугольной пирамиды, когда первый параметр задает высоту пирамиды (например, равную 20 мм), а вторым параметром является следующая величина:

1. Высота боковой грани (22 мм).

2. Длина бокового ребра (26 мм).

3. Угол между основанием и боковой гранью (70°).

4. Угол между основанием и боковым ребром (55°).

5. Расстояние между скрещивающимися ребрами (15 мм).

6. Расстояние между боковой гранью и противолежащей вершиной (20 мм).

На рис. 12.41 со знаком «*» указан также зависимый параметр — длина грани основания пирамиды, построенной по двум заданным параметрам.

Длины ребер основания, показанные на рис. 12.41, могут быть найдены в результате решения планиметрических задач или в результате несложных построений с последующим измерением искомой величины.

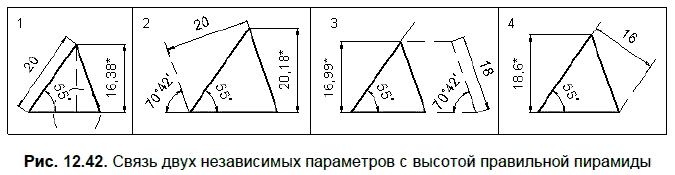
На рис. 12.42 представлены 4 способа создания 3D-модели правильной треугольной пирамиды, когда первый параметр задает угол наклона бокового ребра пирамиды (например, равный 55°), а вторым параметром является следующая величина:

1. Длина бокового ребра (20 мм).

2. Расстояние между боковой гранью и противолежащей вершиной (20 мм).

3. Высота боковой грани (18 мм).

4. Расстояние между скрещивающимися ребрами (16 мм).

На рис. 12.42 со знаком «*» указан также зависимый параметр — высота пирамиды, построенной по двум заданным параметрам.

Условие. Создать 3D-модель правильной треугольной пирамиды с параметрами из варианта 1 на рис. 12.42.

Решение. Для создания модели:

1. Выполните команды Файл | Создать | Деталь. В Дереве модели укажите Плоскость ZX.

2. Нажмите кнопку Эскиз на панели Текущее состояние:

3. В появившейся Компактной панели нажмите кнопку переключения Геометрия для вызова соответствующей Инструментальной панели:

Выберите команду Непрерывный ввод объектов:

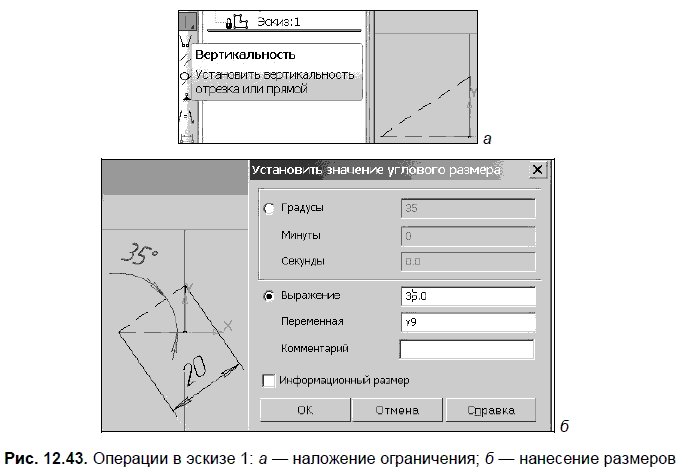
Постройте в эскизе 1 прямоугольный треугольник (для начальных построений в эскизе стиль Основная не использовать). На панели Параметризация выберите команду Вертикальность (рис. 12.43, а) и укажите отрезок, который не должен изменять свое положение при изменении геометрии эскиза 1. Нанесите в эскизе два размера (рис. 12.43, б).

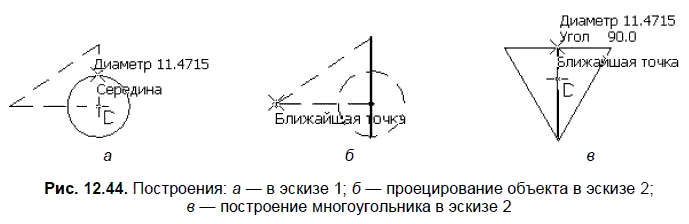
4. На панели Глобальные привязки включите привязку Середина. Используя эту привязку и выбрав команду Окружность, постройте окружность с центром в начале координат и с диаметром, определенным положением середины вертикального катета (рис. 12.44, а). Вертикальный отрезок продолжите до пересечения с нижней частью построенной окружности (рис. 12, 44, б). На панели Геометрия:

выберите команду Точка:

Укажите точку пересечения гипотенузы и горизонтального катета (рис. 12.44, б).

Установите стиль вертикального отрезка: Основная. Завершите эскиз повторным нажатием кнопки Эскиз:

5. В Дереве модели укажите Плоскость XY. Нажмите кнопку Эскиз:

6. В эскизе 2 выполните команды Операции | Спроецировать объект и укажите отрезок из эскиза 1. Измените стиль линии спроецированного отрезка. Выберите команду Многоугольник:

Постройте треугольник с известным центром и привязкой к концам спроецированного в эскиз отрезка (рис. 12.44, в).

7. Закройте эскиз 2 и повторно откройте эскиз 1. Измените стиль Основная вертикального отрезка на любой другой. Закройте эскиз.

8. Нажмите кнопку Операция по сечениям:

на панели Редактирование детали:

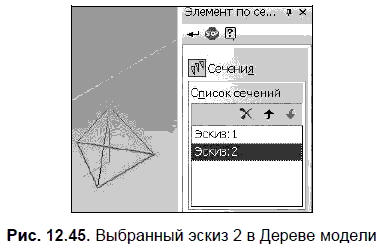
9. В Дереве модели укажите Эскиз: 1 и Эскиз: 2 (рис. 12.45).

Эти названия появятся в списке сечений Панели свойств. Нажмите кнопку Создать объект:

10. После задания Ориентация | Изометрия YZX и включения команды Невидимые линии тонкие на панели Вид получится изображение тетраэдра, показанное на рис. 12.4, а.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Компас 3D. Пирамида (тетраэдр) с шаром.

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.