Как сделать уравнение в отрезках

Уравнение плоскости в отрезках: описание, примеры, решение задач

Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.

Уравнение плоскости в отрезках – описание и примеры

a a + 0 b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + b b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + 0 b + c c = 1 = 1 ⇔ 1 = 1

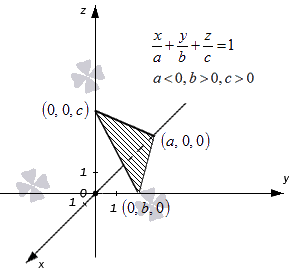
Поясним этот момент, расположив заданные точки на графике.

Проиллюстрируем описанное выше примером.

Решение

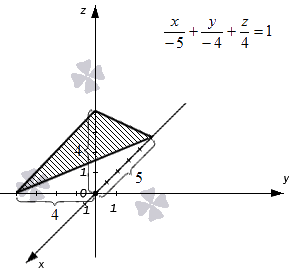
Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.

Решение

Ответ:

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.

Разберем решение примера.

Решение

Источник

Уравнение прямой в отрезках

В данной статье мы рассмотрим уравнение прямой в отрезках. Представим методы преобразования уравнения прямой в отрезках в уравнение прямой в общем виде и обратно. Рассмотрим численные примеры.

Уравнение прямой в отрезках представляется следующей формулой:

где a и b числа, отличные от нуля.

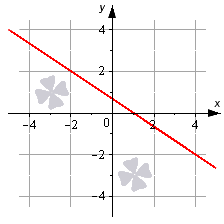
Отметим, что числа a и b в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает прямая на осях Ox и Oy (Рис.1).

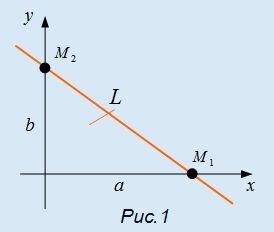Действительно. Подставляя в (1) y=0, получим x=a, если же подставить в (1) x=0, то получим y=b. Таким образом прямая L проходит через точки M₁(a, 0) и M₂(0, b).

Пример 1. Составить уравнение прямой, которая пересекает оси Ox и Oy в точках −1 и 3, соответственно.

Решение. Подставляя значения a=−1 и b=3 в (1), получим:

Приведение уравнения прямой в отрезках к общему виду

Левая часть уравнения (1) приведем к общему знаменателю:

Далее, умножив обе части уравнения на ab, получим:

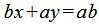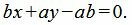Пример 2. Уравнение прямой в отрезках представлено следующим уравнением:

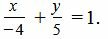Перевести уравнение к общему виду.

Решение. Приведем левую часть уравнения к общему знаменателю:

Умножив обе части уравнения на −20, получим:

Приведение общего уравнения прямой на плоскости к уравнению прямой в отрезках

где A, B, C − отличные от нуля числа.

Сделаем следующие преобразования. Переведем свободный член C на правую часть уравнения и разделим обе части уравнения на −C:

Уравнение (2) можно переписать в следующем виде:

Сделаем следующие обозначения:

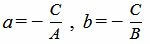Тогда получим уравнение прямой в отрезках (1).

Пример 3. Привести общее уравнение прямой

к уравнению прямой в отрезках.

Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение прямой в отрезках. Воспользуемся формулой (3). Имеем: A=5, B=8, C=−3. Подставив эти значения в формулу (3), получим:

Источник

Уравнение прямой в отрезках: описание, примеры, решение задач

Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.

Уравнение прямой в отрезках – описание и примеры

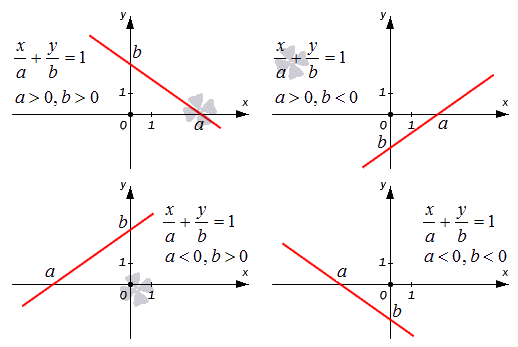
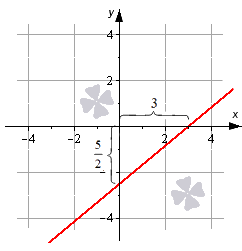
На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.

Решение

Приведение общего уравнения прямой к уравнению прямой в отрезках

Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.

Разберем следующий пример.

Решение

Мы получили уравнение прямой в отрезках.

В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.

Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».

Решение

Действует по заранее описанному алгоритму:

Источник

Уравнение прямой, виды уравнения прямой на плоскости

В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.

Определение уравнения прямой на плоскости

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Общее уравнение прямой линии

Поясним некоторые важные аспекты темы.

Посмотрите на рисунок.

Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Уравнение прямой в отрезках

Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».

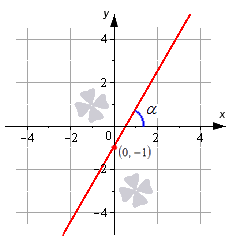
Уравнение прямой с угловым коэффициентом

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Каноническое уравнение прямой на плоскости

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.

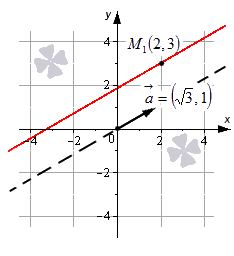
Параметрические уравнения прямой на плоскости

Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

Нормальное уравнение прямой

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Источник

Общее уравнение прямой: описание, примеры, решение задач

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Общее уравнение прямой: основные сведения

указанная теорема состоит из двух пунктов, докажем каждый из них.

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Рассмотрим конкретный пример общего уравнения прямой.

Неполное уравнение общей прямой

Разберем все вариации неполного общего уравнения прямой.

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Решение

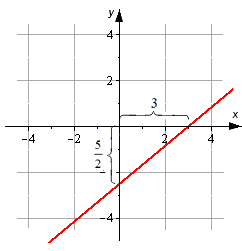
На чертеже изображена прямая, необходимо записать ее уравнение.

Решение

Общее уравнение прямой, проходящей через заданную точку плоскости

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Решение

Решение

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Решение

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Решение

Осуществим переход от общего уравнения к каноническому:

Решение

Произведем нужные действия по алгоритму:

Решение

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

Каноническое уравнение преобразуется к общему по следующей схеме:

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

Решение

Осуществим переход от параметрических уравнений к каноническому:

Перейдем от канонического к общему:

Решение:

Просто перепишем уравнение в необходимом виде:

Составление общего уравнения прямой

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Решение

Решение

Источник