Как узнать что число кратно 15

Признаки делимости на 15: как найти, примеры и задачи с решением

Зачастую при решении задач нужно узнать, делится ли то или иное число на заданную цифру без остатка. Но каждый раз делить его очень долго. К тому же велика вероятность допустить ошибку в расчетах и уйти от правильного ответа. Для того чтобы избежать этой проблемы, были найдены признаки делимости на основные простые или однозначные числа: 2, 3, 9, 11. Но что делать, если нужно произвести деление на другую, большую цифру? Например, как рассчитать признак делимости на 15? Ответ на этот вопрос мы постараемся найти в данной статье.

Как сформулировать признак делимости на 15?

Вам будет интересно: Тангенциальное, или касательное ускорение

Если для простых чисел признаки делимости хорошо известны, то что делать с остальными?

Если число не является простым, то его можно разложить на множители. Например, 33 – это произведение 3 и 11, а 45 – 9 и 5. Существует свойство, согласно которому число делится на данное без остатка в случае, если его можно разделить и на тот, и на другой множитель. Это значит, что любое большое число можно представить в виде простых, и уже исходя из них, формулировать признак делимости.

Итак, нам нужно узнать, можно ли разделить данное число на 15. Для этого рассмотрим его подробнее. Число 15 можно представить, как произведение 3 и 5. Значит, чтобы число делилось на 15, оно должно быть кратно одновременно 3 и 5. Это и есть признак делимости на 15. В дальнейшем мы рассмотрим его подробнее и сформулируем точнее.

Как узнать, что число делится на 3?

Вспомним признак делимости на 3.

Число делится на 3, если сумма его цифр (количество единиц, десятков, сотен и так далее) делится на 3.

Так, например, необходимо узнать, какие из этих чисел можно разделить на 3 без остатка: 76348, 24606, 1128904, 540813.

Конечно, можно просто разделить данные числа в столбец, но это займет немало времени. Поэтому мы воспользуемся признаком делимости на 3.

Таким же образом проанализируем остальные числа:

Ответ: 24 606 и 540 813.

Когда число делится на 5?

Однако признак делимости числа на 15 также включает в себя не только делимость на 3, но и кратность пяти.

Признак делимости на 5 таков: число делится на 5, если оно оканчивается на 5 или на 0.

Например, нужно найти числа кратные 5: 11 467, 909, 670, 840 435, 67 900

Числа 11 467 и 909 не делятся на 5.

Числа 670, 840 435 и 67 900 оканчиваются на 0 или 5, а значит, кратны 5.

Примеры с решением

Итак, теперь мы можем полноценно сформулировать признак делимости на 15: число делится на 15 тогда, когда сумма его цифр кратна 3, а последней цифрой является или 5, или 0. Важно отметить, что оба этих условия должны выполняться одновременно. Иначе мы получим число кратное не 15, а только 3 или 5.

Признак делимости чисел на 15 очень часто нужен для решения контрольных и экзаменационных заданий. Например, зачастую в базовом уровне ЕГЭ по математике встречаются задачи, основанные на понимании именно этой темы. Рассмотрим некоторые их решения на практике.

Среди чисел найдите те, которые делятся на 15.

9 085 475; 78 545; 531; 12 000; 90 952

Итак, для начала отбросим те числа, которые очевидно не удовлетворяют нашим критериям. Это 531 и 90 952. Несмотря на то, что сумма 5+3+1 = 9 делится на 3, число оканчивается на единицу, а значит, не подходит. То же самое касается 90 952, которое оканчивается на 2.

9 085 475, 78 545 и 12 000 удовлетворяют первому критерию, теперь проверим их на соответствие второму.

9+0+8+5+4+7+5 = 38, 38 не делится на 3. Значит, это число является лишним в нашем ряду.

7+8+5+4+5 = 29. 29 не кратно 3, не удовлетворяет условиям.

А вот 1+2 = 3, 3 делится на 3 нацело, это значит, что именно это число и является ответом.

Трехзначное число С больше 700 и делится на 15. Запишите наименьшее такое число.

Итак, по признаку делимости на 15 данное число должно заканчиваться на 5 или 0. Так как на нужно самое маленькое из возможных, возьмем 0 – это будет последней цифрой.

Так как число больше 700, то первой может быть цифра 7 или больше. Помня, что нам следует найти наименьшее значение, выбираем 7.

Чтобы число делилось на 15, должно выполняться условие 7+х+0 = число, кратное 3, где х – количество десятков.

Число 720 – искомое.

Вычеркните из числа 3426578 любые три цифры так, чтобы получившееся число было кратно 15.

Во-первых, искомое число должно оканчиваться на цифру 5 или 0. Значит, последние две цифры – 7 и 8 нужно вычеркнуть сразу.

3+4+2+6+5 = 20, 20 не делится на 3. Ближайшее кратное 3 число – это 18. Для того, чтобы получить его, нужно отнять 2. Вычеркиваем цифру 2.

Получается 3465. Проверим свой ответ, 3465 : 15 = 231.

В данной статье были рассмотрены основные признаки делимости на 15 с примерами. Этот материал должен помочь ученикам с решением заданий такого типа и подобных им, а также понять алгоритм работы с ними.

Источник

Что такое кратное число

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.

Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.

Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.

Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.

Таблицы чисел кратных 2,3,4,5,6,7,9

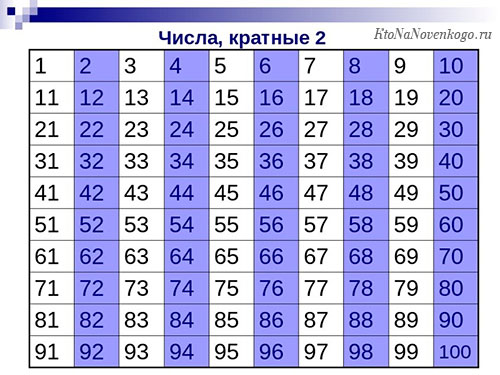
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.

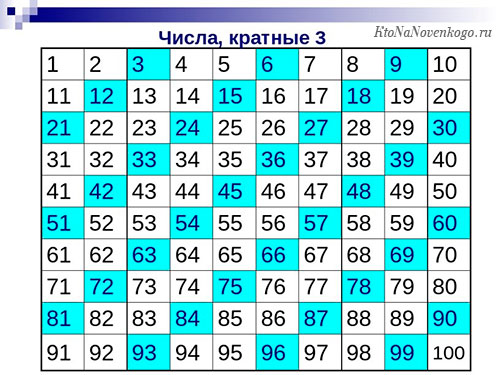
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.

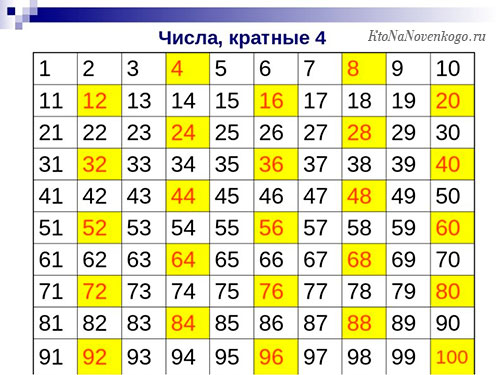
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.

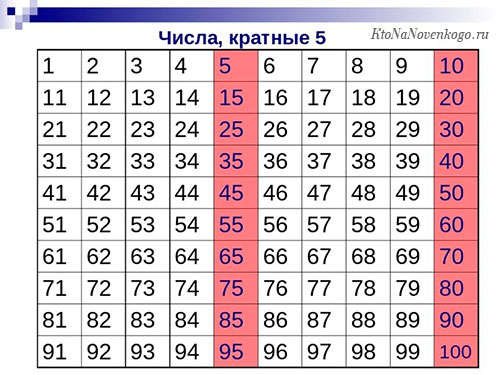
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.

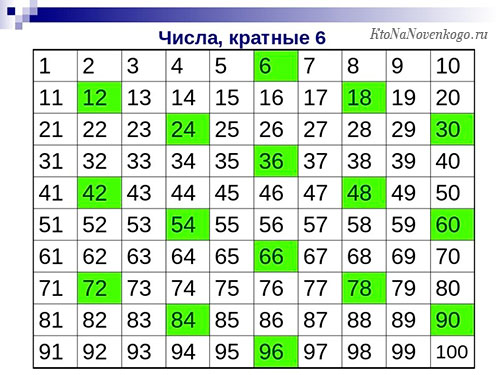
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.

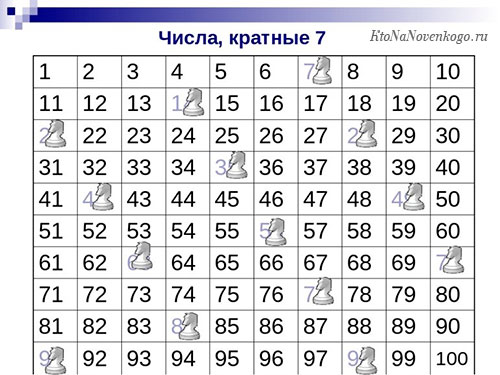
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».

И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.

Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.

Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.

Вместо заключения

А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.

Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.

Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.

Источник

Признаки делимости чисел

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Что такое «признак делимости»

Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.

Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.

Однозначные, двузначные и трехзначные числа

Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.

Трехзначные числа — числа, в составе которых три знака (три цифры).

Чётные и нечётные числа

Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!

Признаки делимости чисел

Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.

Признак делимости на 3. Сумма цифр числа должна делиться на 3.

Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.

Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.

Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.

Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.

Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.

Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.

Источник

Делитель и кратное в математике

Что такое делители и кратные числа

Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.

Выделяют следующие компоненты деления:

Делимое — число, которое делят на несколько частей.

Делитель — число, которое показывает, на сколько частей нужно разделить делимое.

Частное — число, которое является результатом деления.

Умножение частного на делитель дает делимое.

Чтобы получить делитель, нужно делимое разделить на частное.

Д е л и м о е = ч а с т н о е * д е л и т е л ь Д е л и т е л ь = д е л и м о е / ч а с т н о е

Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.

16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.

Делителем числа a называется такое число b, на которое a делится нацело.

Например, 9 : 4 = 2 (остаток 5 ).

В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.

Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9 : 4 = 2 (остаток 5 ) — число 4 не является делителем числа 9.

Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.

Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.

Тогда представим решение данной задачи в виде уравнения:

72 — целое число, без остатка.

Произведение делителей должно дать в результате 144:

72 * 2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.

Ответ: числа 2 и 72 — делители 144.

Число называют кратным, если оно делится на данное число нацело, без остатка.

Например, 15:3 нацело.

Тогда число 15 является кратным 3.

Слово «кратно» синонимично слову «делится».

Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».

Основные понятия и определения

Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.

Делится нацело = без остатка.

Наименьшим делителем любого числа является единица.

Наибольшим делителем числа является само число.

Делителем нуля будет любое число, но сам 0 делителем не будет.

При делении нуля на любое число получаем 0. А делить на ноль нельзя.

У единицы только один делитель — единица.

Другие числа, кроме 1, имеют не меньше двух делителей.

Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.

Наименьшее кратное числа является равным самому числу.

Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.

Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.

Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.

Чем отличаются друг от друга, как найти

Делитель отличается от кратного тем, что:

Чтобы найти делители числа, нужно данное число разложить на множители.

Разложить на множители — представить число в виде произведения целых чисел.

Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.

Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.

Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.

Примеры решения задач

Необходимо найти делители числа 14.

Решить задание можно двумя способами.

Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.

Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.

Ответ: делители числа 14: 1, 2, 7, 14.

Представим 14 в виде произведения чисел:

Делителями будут множители, так как можем разделить 14 нацело на каждый из них.

Ответ: делители 14: 1, 2, 7, 14.

Найдите три числа, кратных 7.

Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.

7 * 1 = 7 — семь кратно семи;

7 * 2 = 14 — 14 кратно 7;

7 * 3 = 21 — 21 кратно 7.

Ответ: числа, кратные 7: 7, 14, 21.

Самостоятельно проверьте, 225 кратно 3 или нет.

Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.

75 — целое число, при делении нет остатка. Тогда 225 кратно 3.

Найдите любое число, делителями которого являются числа 7 и 8.

Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:

Источник