Какая скорость называется второй космической скоростью чему она равна
Вторая космическая скорость
[[Категория:Наука:Статьи без ссылок на источники Ошибка: неправильное время]] К:Наука:Статьи без источников (страна: )
Втора́я косми́ческая ско́рость (параболи́ческая ско́рость, ско́рость освобожде́ния, ско́рость убега́ния) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него. Предполагается, что после приобретения телом этой скорости оно более не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Если тело запущено вертикально вверх со второй космической и более высокой скоростью, оно никогда не остановится и не начнёт падать обратно.
Содержание
Вычисление
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.

Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности небесного тела):
Вторая космическая скорость для различных объектов
| Небесное тело | Масса (по отношению к массе Земли) | 2-я космическая скорость, км/с |
|---|---|---|
| Плутон | 0,002 | 1,2 |
| Луна | 0,0123 | 2,4 |
| Меркурий | 0,055 | 4,3 |
| Марс | 0,108 | 5,0 |
| Венера | 0,82 | 10,22 |
| Земля | 1 | 11,2 |
| Уран | 14,5 | 22,0 |
| Нептун | 17,5 | 24,0 |
| Сатурн | 95,3 | 36,0 |
| Юпитер | 318,3 | 61,0 |
| Солнце | 333 000 | 617,7 |
См. также
Выделить Вторая космическая скорость и найти в:
Вторая космическая скорость
Втора́я косми́ческая ско́рость (параболи́ческая ско́рость, ско́рость освобожде́ния, ско́рость убега́ния) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания круговой орбиты вокруг него. Предполагается, что после приобретения телом этой скорости оно более не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.
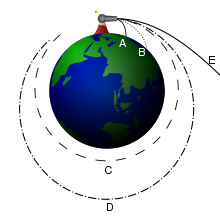
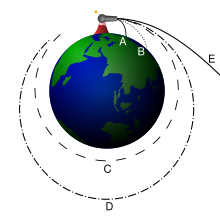
Параболической вторая космическая скорость называется потому, что тела, имеющие при старте скорость, в точности равную второй космической, движутся по дуге параболы относительно небесного тела. Однако, если энергии телу придано чуть больше, его траектория перестает быть параболой и становится гиперболой; если чуть меньше, то она превращается в эллипс. В общем случае все они являются коническими сечениями.
Содержание
Вычисление
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v2 — вторая космическая скорость.
Решая это уравнение относительно v2, получим
Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):
Вторая космическая скорость для различных объектов
См. также
Примечания
Ссылки
 Небесная механика Небесная механика | |
|---|---|
| Законы и задачи | Законы Ньютона • Закон всемирного тяготения • Законы Кеплера • Задача двух тел • Задача трёх тел • Гравитационная задача N тел • Задача Бертрана • Уравнение Кеплера |
| Небесная сфера | Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая • Международная небесная система координат • Сферическая система координат • Ось мира • Небесный экватор • Прямое восхождение • Склонение • Эклиптика • Равноденствие • Солнцестояние • Фундаментальная плоскость |
| Параметры орбит | Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра • Апоцентр и перицентр • Орбитальная скорость • Узел орбиты • Эпоха |
| Движение небесных тел | Движение Солнца и планет по небесной сфере • Эфемериды Конфигурации планет: противостояние • квадратура • парад планет • Кульминация • Сидерический период • Орбитальный резонанс • Период вращения • Предварение равноденствий • Синодический период • Сближение Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл • Покрытие • Прохождение • Либрация • Элонгация • Эффект Козаи • Эффект Ярковского • Эффект Джанибекова |
| Астродинамика | |
| Космический полёт | Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая Формула Циолковского • Гравитационный манёвр • Гомановская траектория • Метод оскулирующих элементов • Приливное ускорение • Изменение наклонения орбиты • Стыковка • Точки Лагранжа • Эффект «Пионера» |
| Орбиты КА | Геостационарная орбита • Гелиоцентрическая орбита • Геосинхронная орбита • Геоцентрическая орбита • Геопереходная орбита • Низкая опорная орбита • Полярная орбита • Тундра-орбита • Солнечно-синхронная орбита • Молния-орбита • Оскулирующая орбита |
Полезное
Смотреть что такое «Вторая космическая скорость» в других словарях:
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см. Параболическая скорость … Большой Энциклопедический словарь
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см … Большая политехническая энциклопедия
вторая космическая скорость — см. Параболическая скорость. * * * ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ, см. Параболическая скорость (см. ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ) … Энциклопедический словарь
Вторая космическая скорость — минимальная скорость v2, необходимая для того, чтобы космический летательный аппарат вышел из сферы гравитационного действия Земли и стал искусственным спутником Солнца. Выражается формулой: Вторая космическая скорость, где G гравитационная… … Астрономический словарь
вторая космическая скорость — antrasis kosminis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. escape cosmic velocity; second cosmic velocity vok. Entweichgeschwindigkeit, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
вторая космическая скорость — antrasis kosminis greitis statusas T sritis fizika atitikmenys: angl. escape cosmic velocity; second cosmic velocity vok. Entweichgeschwindigkeit, f; Entweichungsgeschwindigkeit, f; zweite kosmische Geschwindigkeit, f rus. вторая космическая… … Fizikos terminų žodynas
Вторая космическая скорость — наименьшая скорость (начальная), которую нужно сообщить телу у поверхности Земли, чтобы оно, преодолев действие земного притяжения, навсегда покинуло Землю. В. к. с. равна примерно 11,2 км/сек. Тело, обладающее В. к. с., движется по… … Большая советская энциклопедия
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см. Параболическая скорость … Естествознание. Энциклопедический словарь
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см. Космические скорости … Большой энциклопедический политехнический словарь
Космическая скорость — (первая v1, вторая v2, третья v3 и четвёртая v4) это мин … Википедия
Параболическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Вывод формулы
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v2 — вторая космическая скорость.
Разрешая относительно v2, получим
Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):
См. также
Полезное
Смотреть что такое «Параболическая скорость» в других словарях:
ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ — минимальная скорость, которую нужно сообщить телу массой m (напр., космическому аппарату), чтобы оно могло преодолеть гравитационное притяжение другого тела массой М m (напр., Земли) и, двигаясь по параболической траектории, навсегда покинуть… … Большой Энциклопедический словарь
ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ — см. Космическиескорости. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия
параболическая скорость — минимальная скорость, которую нужно сообщить телу массой т (например, космическому аппарату), чтобы оно могло преодолеть гравитационное притяжение другого тела массой М>>т (например, Земли) и, двигаясь по параболической траектории, навсегда… … Энциклопедический словарь
параболическая скорость — parabolinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Paraboline trajektorija judančio taško ar kūno greitis. atitikmenys: angl. parabolic velocity vok. parabolische Geschwindigkeit, f rus. параболическая скорость, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
параболическая скорость — parabolinis greitis statusas T sritis fizika atitikmenys: angl. parabolic velocity vok. parabolische Geschwindigkeit, f rus. параболическая скорость, f pranc. vitesse parabolique, f … Fizikos terminų žodynas
Параболическая скорость — скорость, которую нужно сообщить тому или иному телу (космическому зонду, частице атмосферы и т.п.), чтобы оно, преодолев притяжение Земли (Луны, планеты и др.), удалилось от неё по параболической орбите. П. с. уменьшается с расстоянием… … Большая советская энциклопедия
Параболическая скорость — тело, движущееся по параболе, в каждой точке своей орбиты имеет скорость, квадрат которой в два раза больше квадрата скорости тела движущегося по кругу, около того же центра притяжения, проходящего через эту точку. Это следует из так наз. закона… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ — миним. скорость, к рую нужно сообщить телу мяссой т (напр., космич. аппарату), чтобы оно могло преодолеть гравитац. притяжение др. тела массой Мт>> (напр., Земли) и, двигаясь по параболич. траектории, навсегда покинуть сферу его гравитац.… … Естествознание. Энциклопедический словарь
ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ — см. Космические скорости … Большой энциклопедический политехнический словарь
Орбитальная скорость — … Википедия
Вторая космическая скорость
Из школьного курса физики мы помним, что первая космическая скорость Земли – это показатель, которого необходимо достичь, чтобы объект мог выйти на эллиптическую орбиту вращения вокруг планеты. Это же, собственно, касается и любого массивного космического тела. В свою очередь, вторая космическая скорость – это предел, необходимый для того, чтобы полностью покинуть гравитационное поле планеты.
Вторая космическая скорость зависит от ряда параметров и для каждого космического объекта – отличается. Давайте рассмотрим, по какому принципу она вычисляется, и разберем примеры для крупных планет Солнечной Системы, Солнца и Луны.
Как рассчитать вторую космическую скорость
Вторая космическая скорость зависит от массы и радиуса небесного тела. Условно можно себе представить, что для ее расчета можно пойти от обратного решения задачи. То есть, вычислить скорость с какой объект будет падать на планету из космоса. По модулю это и будет вторая космическая скорость.
Итак, учитывая закон сохранение кинетической и потенциальной энергий при движении тел, можно вывести такую формулу в падающем объекте на небесное тело:
Где m – масса стартующего объекта, М – масса небесного тела, R – сумма радиуса планеты и высоты расположение объекта над поверхностью, G – гравитационная постоянная, V – искомая вторая космическая скорость. Таким образом, из формулы можно вычислить V:
Это и будет решение нашей задачи со знанием всего двух параметров – радиуса небесного тела и его массы.
Вторая скорость для разных небесных тел
Итак, попробуем на основании выведенной формулы рассчитать вторую космическую скорость для разных небесных тел Солнечной Системы, учитывая что их радиус и массу мы знаем.
Начнем с самого простого – Земли. Радиус нашей планеты равен 6,37 тысяч километров, а масса – 5,97 х 10²³ кг. Подставляем в нашу формулу и получаем – вторая космическая скорость Земли равна 11,2 километра в секунду. Именно до таких цифр нужно разогнать гипотетический объект, чтобы он покинул зону гравитационного притяжения нашей планеты.
Теперь можно перейти к нашей звезде и посчитать вторую космическую скорость для Солнца. Радиус его равен 696 тысяч километров, а масса 1,989 х 10³⁰ кг. Расчеты по формуле дают результат в 617,7 километров в секунду! До такой скорости нужно разогнать предмет, чтобы он смог покинуть нашу Солнечную Систему и попасть в межзвездное пространство.
Теперь попробуем вычислить показатель для остальных планет системы. Итак, радиус и масса Меркурия составляют соответственно 2,438 тысяч километров и 330 х 10²¹ кг. Подставив в формулу цифры, получаем вторую космическую скорость Меркурия 4,3 км/с.
Идем далее и получаем такие цифры – вторая космическая скорость Венеры – 11,2 километров в секунду, Марса – 5,0 км/с, Юпитера – 61 км/с, Сатурна – 36 км/с, Нептуна – 24 км/с, Урана – 22 км/с, Луна – 2,4 км/с.
Таким образом, мы видим, что преимущественно чем массивнее планета (а вернее, чем плотнее, потому что радиус тоже важен) – тем больше нужна скорость, чтобы объект мог вырваться за пределы гравитационного влияния.
Показательными и интересными также являются примеры третей и четвертой космических скоростей. Что это за параметры? Если говорить грубо – то третья космическая скорость, это вторая космическая для Солнца, но высчитываемая вблизи Земли. Простыми словами – какую скорость нужно развить с Земли, чтобы покинуть Солнечную Систему? Посчитав по формуле, получим 16,65 километров в секунду.

Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
 otvet_plus
otvet_plus
Про отличия и различия между похожими вещами
Журнал для эрудитов
Первая космическая скорость
Это скорость физического объекта, с которой он может вращаться вокруг Земли, не падая на нее и не отрываясь в пространство. Первая космическая скорость обеспечивает равновесное положение тела, движущегося по круговой траектории вблизи поверхности Земли. При отсутствии тормозящих факторов такое движение может продолжаться бесконечно долго. При этом масса самого вращающегося объекта значения не имеет, а радиус окружности вращения должен немного превышать радиус Земли.
Для того чтобы тело, находящееся на поверхности Земли, приобрело первую космическую скорость, его нужно разогнать. При этом усилие разгона должно быть перпендикулярно радиусу, и вектор приложения силы должен быть направлен по касательной к окружности вращения.
Самым наглядным примером вращательного движения может служить любой предмет, привязанный к веревке. Раскрутите его, и он будет вращаться «по орбите» с радиусом, равным длине веревки. Упругость веревки противодействует центробежной силе и равна ей по величине. Отпустите веревку, и ваш предмет улетит вместе с веревкой в направлении, которое тело имело в момент отпускания верёвки.
Сила – понятие векторное
Из школьного курса физики известно, что сила – это понятие векторное, имеет не только величину, но и направление. Роль центробежной силы для искусственных космических объектов первоначально играет внешнее ускорение. Эту роль выполняют реактивные двигатели ракеты-носителя. Они-то и «выталкивают» объект на орбиту – умозрительную линию окружности, по которой движется объект.
Как высчитать первую космическую скорость
На объект, находящийся на орбите, действуют две силы – центробежная сила и сила тяготения Земли. Раз объект не улетает в пространство, и не падает на землю, то эти силы находятся в равновесии.
Центробежная сила вычисляется по формуле:
m – масса точки
v – линейная скорость точки
r – радиус траектории
Сила притяжения Земли вычисляется по формуле:
G – гравитационная составляющая = 6,67259•10?11 м?•кг?1•с?2
М – масса Земли = 5,97•1024 кг
m – масса объекта – пренебрежимо мала относительно массы Земли
r – радиус Земли = 6371 км
Тогда равновесную скорость вращения объекта (первую космическую скорость) можно найти из уравнения:
Подставляя численные значения для Земли, получим:
V = 7,9 километров в секунду!
Для неискушенного в физике-математике человека не очень понятно, но оно и не надо. Важно, что этот закон действует и является абсолютно верным для Земли.
Надо иметь в виду, что это чисто математическая формула, в которой предполагается, что Земля абсолютно гладкий шар правильной формы, на котором отсутствует атмосфера, магнитные поля, гравитация других планет и прочие тормозящие факторы, воздействующие на тело в реальной жизни. Она верна для траекторий, с радиусом, почти равным радиусу Земли. Если же радиус полета тела будет больше, то величина первой космической скорости будет уменьшаться. То есть, чем дальше объект от поверхности Земли, тем меньше величина первой космической скорости. Посмотрите таблицу:
Чтобы было легче вывести космические объекты на околоземные орбиты, используют скорость вращения самой Земли. Корабли запускают только в направлении вращения Земли. При том, желательно, чтобы точка старта была как можно ближе к экватору, где линейная скорость максимальна. Именно поэтому космодром Байконур построен на юге Казахстана, а американский космодром расположен во Флориде, а не на Аляске.
Вторая космическая скорость
Это минимальная скорость, при достижении которой объект, движущийся по вращательной орбите вокруг Земли, может преодолеть силу притяжения планеты и улететь в пространство. Её еще называют скоростью убегания.
Читать далее: про вторую, третью и четвертую космические скорости








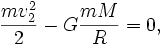
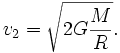
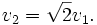
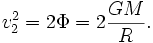

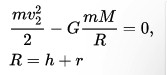
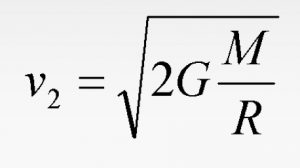
 otvet_plus
otvet_plus