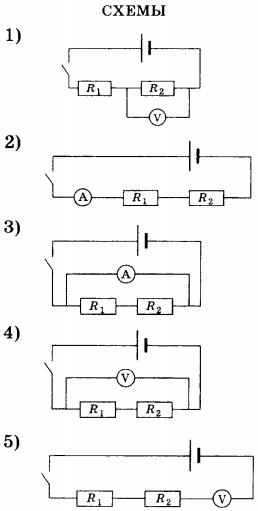
Какие физические величины сохраняются при параллельном соединении проводников чему равна

Последовательное и параллельное соединение

Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.

Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м 2

l – длина проводника, м

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

сила тока через последовательное соединение проводников

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

Если бы у нас еще были резисторы, соединенные параллельно, то для них

В этом случае, сила тока в цепи будет равна:

Задача

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение

Воспользуемся формулами, которые приводили выше.

Если бы у нас еще были резисторы, соединенные параллельно, то для них

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

2-ой способ найти I

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.

I=U/R_общее = 10/1,25=8 Ампер.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Источник

Параллельное и последовательное соединение проводников.

Для параллельного соединения проводников справед­ливы следующие соотношения:

а) электрический ток, поступающий в точку А разветвления проводников (она называется также узлом), равен сумме токов в каждом из элементов цепи:

б) напряжение U на концах проводников, соединенных параллельно, одно и то же:

в) при параллельном соединении проводников складываются их обратные сопротивления:
г) сила тока и сопротивление в проводниках связаны соотношением:

.

Для последовательного соединения проводников в цепи справедливы следующие соотношения:

.

а) для общего тока I:

где I₁ и I ₂ — ток в проводниках 1 и 2 соответственно; т. е. при последовательном соединении про­водников сила тока на отдельных участках цепи одинакова;

б) общее напряжение U на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:

в) полное сопротивление R всего участка цепи равно сумме последовательно соединенных сопротивлений:

г) также справедливо соотношение:

.

Источник

Последовательное и параллельное соединения проводников

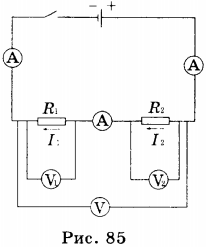
1. Потребители электрической энергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).

Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.

При последовательном соединении проводников ток проходит через все лампочки, при этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд, т.е. заряд не скапливается ни в какой части проводника. Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: ​ \( I_1=I_2=I \) ​.

Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: ​ \( R_1=R_2=R \) ​. Это следует из того, что при последовательном соединении проводников их общая длина увеличивается, она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.

По закону Ома напряжение на каждом проводнике равно: ​ \( U_1=IR_1 \) ​, ​ \( U_2=IR_2 \) ​, а общее напряжение равно ​ \( U=I(R_1+R_2) \) ​. Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: ​ \( U=U_1+U_2 \) ​.

Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.

2. Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.

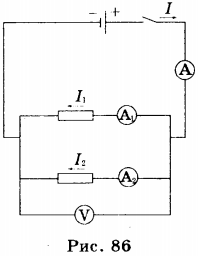
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).

Поэтому вольтметр, подключенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким образом, напряжение на концах всех параллельно соединённых проводников одно и то же: ​ \( U_1=U_2=U \) ​.

При параллельном соединении проводников электрическая цепь разветвляется, в данном случае в точке В. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: ​ \( I=I_1+I_2 \) ​.

При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление ​ \( r \) ​, то их общее сопротивление равно: ​ \( R=r/2 \) ​. Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения, соответственно уменьшается сопротивление.

Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно: они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них и соответствие суммарной силы тока предельно допустимой силе тока.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Напряжения на резисторах соответственно ​ \( U_1 \) ​ и ​ \( U_2 \) ​.

По какой из формул можно определить напряжение U на участке АВ?

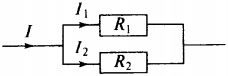
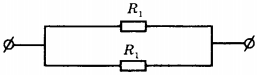
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

1) ​ \( I=I_1=I_2 \) ​
2) \( I=I_1+I_2 \)
3) \( U=U_1+U_2 \)
4) \( R=R_1+R_2 \)

3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R> и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

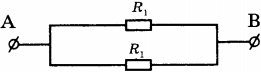
5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением ​ \( R_1 \) ​. По какой из формул можно определить общее сопротивление цепи ​ \( R \) ​?

6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов ​ \( R_1 \) ​ и ​ \( R_2 \) ​ равны. Чему равно сопротивление каждого резистора?

1) 81 Ом
2) 18 Ом
3) 9 Ом
4) 4,5 Ом

7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?

1) 1/3 Ом
2) 3 Ом
3) 9 Ом
4) 27 Ом

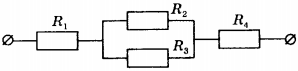
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ​ \( R_1 \) ​ = 1 Ом, ​ \( R_2 \) ​ = 10 Ом, ​ \( R_3 \) ​ = 10 Ом, ​ \( R_4 \) ​ = 5 Ом?

1) 9 Ом
2) 11 Ом
3) 16 Ом
4) 26 Ом

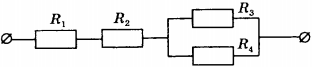
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 3 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 10 Ом?

1) 9 Ом
2) 10 Ом
3) 14 Ом
4) 24 Ом

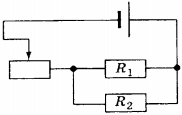
10. Если ползунок реостата (см. схему) переместить влево, то сила тока

1) в резисторе ​ \( R_1 \) ​ уменьшится, а в резисторе ​ \( R_2 \) ​ увеличится
2) увеличится в обоих резисторах
3) в резисторе ​ \( R_1 \) ​ увеличится, а в резисторе ​ \( R_2 \) ​ уменьшится
4) уменьшится в обоих резисторах

11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?

Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) сопротивление реостата 2
Б) сила тока в цепи
B) напряжение на резисторе 1

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе \( R_1 \) ​ и \( R_2 \)
Б) напряжение на резисторе \( R_2 \)
B) общее напряжение на резисторах \( R_1 \) ​ и \( R_2 \)

Часть 2

13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов ​ \( R_1 \) ​ = 10 Ом, \( R_2 \) = 5 Ом, \( R_3 \) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?

Источник

Последовательное и параллельное соединение проводников — формулы и примеры расчетов

В электроцепи ток движется от источника к нагрузке. В этих схемах применяются всевозможные элементы, имеющие конкретное сопротивление. В соответствии с выполняемыми задачами в электроцепях может практиковаться последовательное и параллельное соединение проводников. Однако иногда приходится использовать сочетание этих видов подключения. Такой вариант назван смешанным. На этапе проектирования электроцепей необходимо учитывать все их особенности.

Последовательное соединение

При данном типе подключения проводники монтируются один за другим. В результате конец первого является началом второго и т. д. Особенность такого соединения заключается в отсутствии разветвлений. Со свойствами созданной этим способом электроцепи можно познакомиться на примере схемы с двумя потребителями, выключателем и источником питания. Последовательное подсоединение проводников обладает несколькими особенностями:

Этот тип подключения предполагает возможность использования любого числа нагрузок. На этапе конструирования цепи следует помнить, что показатель общего сопротивления обязательно будет превышать уровень сопротивления отдельного участка. Этот факт объясняется увеличением длины проводов. В результате можно получить формулу для определения сопротивления всей цепи: R = R * n. В ней n равно числу проводников.

Что касается напряжения (U), то этот показатель на любом участке электроцепи будет меньше суммарного показателя в n раз. Например, если в бытовую электросеть с U = 220 В подключить 5 лампочек равной мощности, то напряжение на каждом элементе составит 44 вольта.

Также в процессе конструирования электроцепей важно помнить еще об одной важнейшей особенности последовательного подсоединения. Если в процессе работы выходит из строя даже один проводник, то ток не сможет проходить по всей схеме. Отличным примером, иллюстрирующим это свойство, будет ёлочная гирлянда. Достаточно сгореть одной лампе, и вся конструкция перестанет функционировать. Чтобы обнаружить вышедший из строя элемент, придется проверить всю гирлянду.

Параллельное подключение

Этот тип подсоединения предполагает установку проводников в общих начальных и конечных точках. В результате нагрузки монтируются параллельно, а их количество может быть любым. Для исследования главных свойств такой электроцепи необходимо собрать простую схему, состоящую из источника питания, выключателя и двух ламп. Ко всем нагрузкам также необходимо подключить по амперметру. Еще один прибор этого типа предназначен для измерения показателя общего сопротивления.

Если замкнуть ключ, то измерительные приборы, подсоединенные к нагрузке, покажут значение токовой нагрузки I1 и I2. На общем амперметре в такой ситуации можно будет увидеть суммарное значение токов на каждом из двух участков схемы. Это существенно отличает параллельное соединение от последовательного. В случае если одна нагрузка выходит из строя, то остальные продолжат свою работу. Именно поэтому в бытовых электросетях используется параллельное подсоединение.

Благодаря применению аналогичной схемы, появится возможность определить напряжение при параллельном соединении. Для этого нужно добавить в нее еще один прибор — вольтметр. Полученный с его помощью результат измерения будет общим для любого участка схемы. После этого можно провести расчет параллельного соединения резисторов. Чтобы решить такую задачу, нужно применить закон Ома. Он гласит, что сила тока равна отношению напряжения к сопротивлению.

Это позволяет вывести следующую формулу — U/R = U1/R1 + U2/R2. В ней R и U — показатели суммарного сопротивления и напряжения электроцепи соответственно. U1, U2, R1 и R2 — значения напряжения и сопротивления на первом и втором потребителе. Так как электроток одинаков для всей схемы, то формула для определения сопротивление при параллельном соединении примет вид — 1/R = 1/R1 + 1/R2.

Это говорит о том, что при этом виде подсоединения потребителей сопротивление имеет невысокое значение. Следовательно, токовая нагрузка тока существенно увеличится.

Данный факт необходимо учитывать при подключении к домашней электрической сети большого числа электроприборов. В такой ситуации возможен перегрев проводов.

Основные законы

Проектирование электрических цепей предполагает наличие хороших знаний основных закономерностей последовательного и параллельного подключения нагрузки. Это касается не только закона Ома, но и постулатов Кирхгофа. Эти физики внесли большой вклад в развитие электротехники. Для более простого восприятия основных законов все формулы стоит рассматривать в следующей последовательности:

В соответствии с первым законом Кирхгофа, алгебраическая сумма токов в узле всегда равна нулю. Благодаря этому, можно получить формулу для нахождения эквивалентного сопротивления цепи, если известно сопротивление каждой нагрузки. Она имеет следующий вид: Ro =R1*R2 / R1+R2.

Для последовательного соединения нагрузок применим второй закон Кирхгофа. Согласно ему, сумма ЭДС в замкнутом электрическом контуре равна сумме падений напряжений на каждой нагрузке. В результате общее сопротивление можно определить с помощью следующей формулы: Ro = R1 + R2.

Также можно рассчитать и индуктивность при различных видах соединения катушек. В случае с последовательным все довольно просто, достаточно использовать следующую формулу: Lo = L1 + L2. По сути, вместо двух элементов можно установить один с соответствующим показателем индуктивности.

При параллельном подсоединении катушек ситуация усложняется, так как возможны три варианта:

Сегодня часто для расчета этих и других показателей, например, емкости конденсатора, можно использовать онлайн-калькулятор.

Особенности применения

Каждый из методов подключения нагрузки нашел свое применение в быту и промышленности. Параллельный способ целесообразно использовать в ситуации, когда электроприбор требуется целенаправленно отключать. Примером здесь может стать электрический звонок, соединенный последовательно с источником питания и кнопкой. В соответствии с этим же принципом работает и ручной фонарик, состоящий из светодиода, ключа и батарейки.

Однако последовательное включение приборов не всегда позволяет решить поставленные задачи. В каждой квартире присутствует большое количество осветительных приборов. Если все их соединить последовательно, то они будут включаться и отключаться одновременно, что требуется крайне редко. Именно люстры принято подключать параллельно. В результате у потребителя появится возможность активировать нужное в данный момент количество ламп. Благодаря этому, достигается требуемая освещенность помещения и экономится электрическая энергия.

В быту чаще всего используется смешенное подключение нагрузок. Этот вид подсоединения проводников является сочетанием параллельного и последовательного соединения. При этом на стадии проектирования электросети крайне важно учитывать все преимущества и недостатки каждого типа подсоединения. Для определения необходимых показателей общую цепь следует разделить на простые участки, а полученные результаты затем суммируются.

Источник