Какие ученые предполагали что пространство вселенной евклидово

Геометрия глобального пространства-времени Ч 4

Целью настоящей статьи является постановка и попытка решения самой глобальной и фундаментальной проблемы всей физики.
Такой проблемой является вопрос о том, каким образом можно естественнонаучным путем объяснить тот факт, что все физические законы природы неизменны во времени и одинаковы во всем пространстве Вселенной. До сих пор эту проблему физики даже не осмеливались всерьез ставить на повестку дня, за исключением разве что Демокрита с его идеей атомов, как фундаментальных кирпичиков мироздания. С тех пор в философском смысле физики практически не продвинулись в указанном направлении и объективный идеализм в форме различных религий до сих пор в этом вопросе на раз кладет современную физику на обе лопатки. Справедливости ради все-таки надо отметить, что постепенное постижение нами фундаментальных законов физики постоянно приближает нас к правильной постановке и правильному решению указанной проблемы.

Решение поставленной проблемы на мой взгляд невозможно также и без выяснения и определения геометрии глобального пространства-времени Вселенной. На мой взгляд именно единство в пространстве и неизменность во времени законов эволюции пространства Вселенной и обеспечивает вкупе с «Принципом нелокальной связанности Вселенной» неизменность всех физических законов во времени. Для того, чтобы выяснить указанную геометрию, нам необходимо уйти от постулируемого общей теорией относительности невероятно усложняющего геометрическую картину Вселенной пространственно-временного многообразия и равноправия всех инерциальных систем отсчета. Это необходимо, чтобы понять каким образом изменяется и развивается неевклидовая (криволинейная) геометрия глобального пространства в неком глобальном времени общем для всех точек геометрии этого глобального пространства, а потому выделяющем глобальное пространство в качестве абсолютной выделенной системы отсчета. При этом для каждой отдельной собственной (покоящейся)точки геометрии этого глобального пространства оказывается возможным ввести свою абсолютную локальную и уже евклидовую инерциальную систему отсчета, покоящуюся относительно данной точки, время в которой течет также, как и глобальное время. Для любого движущегося наблюдателя его собственное время определяется через глобальное время и его скорость относительно глобального пространства. Таким образом локальное (предельно малое) приращение времени для движущегося наблюдателя, находящегося в данный момент времени в некоторой собственной (покоящейся)точке глобального пространства, определяется через соответствующее приращение времени в указанной абсолютной евклидовой локальной системе отсчета в этой точке, которое равно приращению глобального времени (в силу локально одинакового течения времени), точно так же как и в специальной теории относительности, поскольку четырехмерная метрика глобального пространства-времени является для непрерывного пространства-времени локально приводимой к метрике Минковского.

Для решения указанной проблемы важным также является вопрос о том, может ли некое глобальное материальное физическое тело (например глобальная черная или белая дыра Вселенной), существующее в глобальном пространстве-времени Вселенной, определять и обеспечивать наблюдаемые характеристики этого пространства-времени и, с учетом нелокальной связанности Вселенной, упомянутую неизменность и одинаковость всех физических законов природы во всем пространстве-времени Вселенной за счет того, что все свойства пространства-времени и все физические законы природы определяются физическими характеристиками этого глобального материального физического тела.

Полагаю, что само так называемое базовое бесконечное Евклидово пространство Вселенной, получаемое, как в рамках «Общей теории относительности», так и в рамках «Теории глобального времени», как пространство с нулевой энергией, есть ни что иное, как математическая абстракция, не соответствующая реальности. Это очевидно уже в рамках квантовой гипотезы самой «Теории глобального времени», поскольку квантовый подход изначально исключает реальность абсолютно нулевой энергии.

При этом каждый конкретный отрезок, соединяющий центр симметрии такого четырехмерного гиперполнотория с каждой конкретной точкой его трехмерной поверхности следует рассматривать как локальное время в этой точке. Поскольку реальная трехмерная поверхность такого четырехмерного гиперполнотория в реальной Вселенной представляет собой реальное трехмерное пространство Вселенной, то эта поверхность является реально неоднородной в смысле нарушения центральной сферической и осевой симметрии. Эта неоднородность вызвана во-первых, наличием видимой материи и связанных с нею гравитационных взаимодействий и связанных с ее движением релятивистских явлений, а во-вторых, эта неоднородность вызвана также иными собственными деформациями этой поверхности, которые наблюдаются в виде темной материи. Указанная неоднородность и приводит к тому, что для одного и того же глобального времени в различных точках реального трехмерного пространства Вселенной локальное время является неодинаковым. Каждая элементарная частица во Вселенной имеет свое собственное локальное время. Это выражается в частности в «парадоксе близнецов», а также в том, что атомы соединенные в молекулы и кристаллы не разлетаются, также и в том, что не разлетаются тела связанные гравитацией и иными взаимодействиями. С учетом перехода к привычным нам размерностям это локальное время определяем по формуле r3=t*C, где r3 является длиной отрезка, соединяющего центр симметрии (в четырехмерном пространстве) такого трехмерного гипертора с соответствующей конкретной точкой его поверхности, а t является локальным временем в этой точке.

Говоря о возможных геометриях реального пространства-времени Вселенной практически все ученые упускают вопрос о том, почему все основные физические константы и соответственно все физические законы одинаковы и неизменны во всей Вселенной во все времена.

Формально к соотношениям масштаба можно отнести и вышеупомянутую формулу R3=T*C, однако полагаю, что универсальная константа C, совпадающая, по-видимому, со скоростью света в вакууме, сама определяется иными, а именно базовыми соотношениями масштаба, например соотношением глобальной инерционной массы и глобальной энергии Вселенной, определяемой формулой E=M*C*С

Источник

Евклидово пространство

Евклидовы пространства имеют долгую историю и множество приложений. Связи между этим инструментом и остальной математикой многочисленны и разнообразны, от логики и алгебры до неевклидовой геометрии. Этому аспекту посвящена статья « Евклидова геометрия ».

Резюме

Геометрия

Евклидово пространство и двойные точки

В рамках построения векторов с использованием классов эквивалентности бипоинтов на аффинном пространстве может быть получено первое определение скалярного произведения. Норма вектора соответствует длине репрезентативной двойной точки, угол двух векторов соответствует углу двух репрезентативных точек с одинаковым началом. Тогда формула, дающая скалярное произведение, следующая:

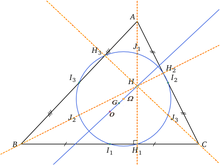
Геометрия треугольника

Формализация и первые свойства

Определения

Мы говорим, что два вектора ортогональны, если их скалярное произведение равно нулю. Определив скалярное произведение, оно не является вырожденным : нулевой вектор является единственным вектором, ортогональным самому себе, и тем более единственным ортогональным ко всему пространству.

Примеры

Неравенства Коши-Шварца и Минковского

Две разметки широко используются при изучении евклидовых пространств.

Алгебраические свойства

Характеристика полярной формой

Сразу выводим следующую характеристику:

Следовательно, первое утверждение сразу же, как и, наоборот, существование скалярного произведения P (достаточно выбрать такое, для которого база B ортонормирована). Уникальность P проистекает из тождеств поляризации и из того факта, что норма полностью определяется ( однородностью ) своей единичной сферой.

Существует четвертый критерий, более прямой, чтобы определить, является ли норма евклидовой, без восстановления ее скалярного произведения:

Ортонормированный базис

Ортогональная проекция

Процесс Грама-Шмидта

Ортогональность и выпуклость

Двойное пространство и билинейная форма

Отображение φ из E в двойственном ему E *, которое с любым вектором x из E связывает линейную форму x *, определяемую следующим образом:

\ rangle>

Ассистент эндоморфизма

На евклидовом пространстве E для любого эндоморфизма а существует единственный эндоморфизм а * такой, что

Таким образом, этот автоморфизм L ( E ) является симметрией относительно подпространства симметрических эндоморфизмов относительно дополнительного подпространства антисимметрик.

Связь, индуцированная скалярным произведением между билинейными формами и эндоморфизмами, имеет множество приложений в самых разных областях (см., В частности, спектральную теорему статьи в случае, когда формы и эндоморфизмы симметричны).

Построение евклидовых пространств

Как часто бывает в алгебре, данные евклидовых пространств позволяют строить новые.

Подпространство, пространство продукта

Фактическое пространство

Тензорное произведение

Таким образом, эта билинейная форма наследует симметрию двух скалярных произведений, и если ( e _i ) является ортонормированным базисом E ₁ и ( f _j ) ортонормированным базисом E _2, то базис ( e _i ⊗ f _j ) E ₁ ⊗ E ₂ ортонормирован для этой формы, что доказывает, что это скалярное произведение.

Эндоморфизм

Этот скалярный продукт выражается просто благодаря понятиям дополнения и следа :

Для этого скалярного произведения симметрия a ↦ a * является ортогональным автоморфизмом L ( E ).

Топология

Характеризация ортогональной группой

Конечномерные нормированные векторные пространства

Обобщения

Источник

Евклидово пространство

Смотреть что такое «Евклидово пространство» в других словарях:

ЕВКЛИДОВО ПРОСТРАНСТВО — конечномерное векторное пространство с положительно определённым скалярным произведением. Является непосредств. обобщением обычного трёхмерного пространства. В Е. п. существуют декартовы координаты, в к рых скалярное произведение ( ху )векторов х … Физическая энциклопедия

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называется n мерное векторное пространство, в котором определено скалярное произведение … Большой Энциклопедический словарь

Евклидово пространство — [Eu­c­lidean space] см. Многомерное (n мерное) векторное пространство, Векторное (линейное) пространство … Экономико-математический словарь

евклидово пространство — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN Cartesian space … Справочник технического переводчика

Евклидово пространство — (также Эвклидово пространство) в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3. В современном понимании, в более общем… … Википедия

евклидово пространство — пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называют n мерное векторное пространство, в котором определено скалярное произведение. * * * ЕВКЛИДОВО ПРОСТРАНСТВО ЕВКЛИДОВО… … Энциклопедический словарь

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства к рого изучаются в евклидовой геометрии. В более широком понимании Е. п. наз. n мерное векторное пространство, в к ром определено скалярное произведение … Естествознание. Энциклопедический словарь

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства к рого описываются аксиомами евклидовой геометрии. В более общем смысле Е. п. конечномерное действительное векторное пространствоRn со скалярным произведением( х, у), х, к рое в надлежащим образом выбранных координатах… … Математическая энциклопедия

Евклидово пространство — (в математике) пространство, свойства которого описываются аксиомами евклидовой геометрии (См. Евклидова геометрия). В более общем смысле Е. п. называется n мepное Векторное пространство, в котором возможно ввести некоторые специальные… … Большая советская энциклопедия

Источник

ЕВКЛИДОВО ПРОСТРАНСТВО

Полезное

Смотреть что такое «ЕВКЛИДОВО ПРОСТРАНСТВО» в других словарях:

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называется n мерное векторное пространство, в котором определено скалярное произведение … Большой Энциклопедический словарь

Евклидово пространство — пространство, свойства которого описываются аксиомами евклидовой геометрии. Упрощенно можно определить евклидово пространство, как пространство на плоскости или в трехмерном объеме, в которых заданы прямоугольные (декартовы) координаты, а… … Начала современного естествознания

Евклидово пространство — [Eu­c­lidean space] см. Многомерное (n мерное) векторное пространство, Векторное (линейное) пространство … Экономико-математический словарь

евклидово пространство — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN Cartesian space … Справочник технического переводчика

Евклидово пространство — (также Эвклидово пространство) в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3. В современном понимании, в более общем… … Википедия

евклидово пространство — пространство, свойства которого изучаются в евклидовой геометрии. В более широком понимании евклидовым пространством называют n мерное векторное пространство, в котором определено скалярное произведение. * * * ЕВКЛИДОВО ПРОСТРАНСТВО ЕВКЛИДОВО… … Энциклопедический словарь

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства к рого изучаются в евклидовой геометрии. В более широком понимании Е. п. наз. n мерное векторное пространство, в к ром определено скалярное произведение … Естествознание. Энциклопедический словарь

ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойства к рого описываются аксиомами евклидовой геометрии. В более общем смысле Е. п. конечномерное действительное векторное пространствоRn со скалярным произведением( х, у), х, к рое в надлежащим образом выбранных координатах… … Математическая энциклопедия

Евклидово пространство — (в математике) пространство, свойства которого описываются аксиомами евклидовой геометрии (См. Евклидова геометрия). В более общем смысле Е. п. называется n мepное Векторное пространство, в котором возможно ввести некоторые специальные… … Большая советская энциклопедия

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Евклидово пространство

Одной из важнейших задач геометрии является задача измерения расстояния между двумя объектами. В произвольном линейном пространстве мы пока не можем определить насколько «близки» между собой объекты. В настоящем разделе понятие расстояния между двумя векторами — элементами линейного пространства — будет вводиться посредством скалярного произведения векторов. Насколько обоснован такой порядок введения понятий:

Определения

Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:

Свойства

Теорема. Имеет место неравенство Коши–Буняковского:

С помощью скалярного произведения, введенного в предыдущем пункте, можно доказать справедливость интегральной формы неравенства:

Теорема. Имеет место неравенство треугольника

Пример. Найти расстояние между полиномами

Теперь прокомментируем последний пример. В разделе, посвященном полиному одной переменной, имеется теорема о непрерывной зависимости корней полинома от его коэффициентов. Смысл этого результата в следующем: если коэффициенты полиномов

Подводя итог приведенным рассуждениям, можно только повторить: метод, выбираемый для оценки близости между объектами, может зависеть от поставленной задачи. Микроскоп не пригоден для наблюдения за большими объектами, а телескоп — за малыми.

Следующий результат также имеет название, взятое из планиметрии, где он формулируется так: сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.

Теорема. В евклидовом пространстве имеет место равенство параллелограмма

Ортогонализация

Чему равно расстояние между двумя векторами ортонормированного базиса?

Пример. Ортогонализовать систему векторов

Пример. Пусть в пространстве полиномов скалярное произведение задается формулой

Следующая теорема устанавливает связь между двумя ортонормированными базисами в одном и том же пространстве.

Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.

Матричный формализм алгоритма Грама-Шмидта: QR-разложение

Пример. Для матрицы из предыдущего примера имеем:

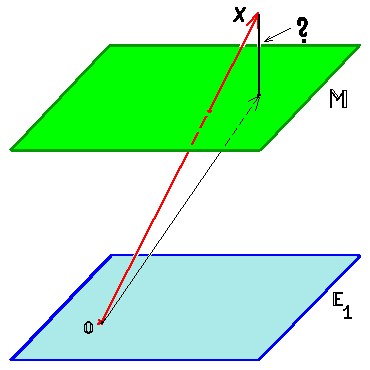
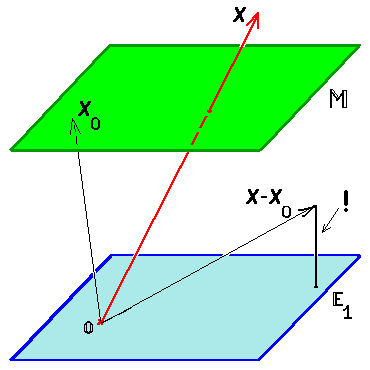
Расстояние от точки до многообразия

Пример. Множество

Доказать, что в пространстве квадратных матриц со скалярным произведением, заданным формулой

Вычисление расстояния

Альтернативный способ вычисления расстояния от точки до линейного многообразия, заданного системой линейных уравнений ☞ ЗДЕСЬ.

Доказательство ☞ ЗДЕСЬ.

Подводя итог: определители Грама полностью решают задачу о вычислении расстояния от точки до линейного подпространства в любом евклидовом пространстве; этот результат легко обобщается на произвольное линейное многообразие.

Вычисление расстояния между линейными многообразиями (и некоторыми другими объектами, заданными алгебраическими уравнениями) ☞ ЗДЕСЬ.

Угол между вектором и линейным многообразием

Эта теорема сводит задачу к решенной в предыдущих пунктах задаче вычисления расстояния от вектора до подпространства, только теперь интерес смещается от ортогональной составляющей вектора к его ортогональной проекции.

Свойства матрицы Грама

Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.

Доказательство ☞ ЗДЕСЬ

Матрица Грама линейно независимой системы векторов является положительно определенной. Матрица Грама произвольной системы векторов является положительно полуопределенной.

Дальнейшие свойства матрицы и определителя Грама ☞ ЗДЕСЬ

Задачи

Источник

Материалы этого раздела составлены на основе книги

Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969

Источник