Какие углы называют смежными чему равна сумма смежных углов

Углы. Смежные углы.

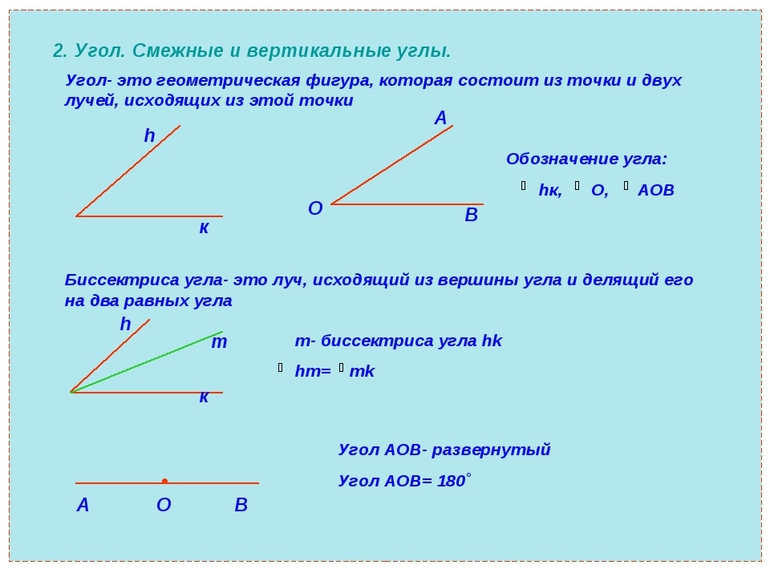
Какие углы называются смежными?

Смежными углами называется пара углов с общей вершиной и одной

общей стороной. 2 оставшиеся стороны делают продолжение друг

другу, образовывая прямую линию. Для угла 135 градусов смежным

будет угол равный 45 градусам. Для угла x градусов смежным

является угол (180 – x) градусов.

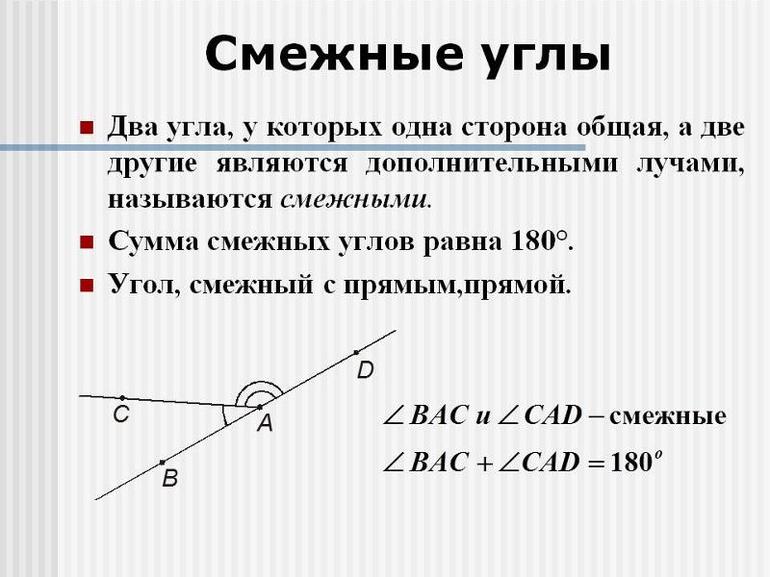
Два смежных угла — это углы, с одной общей стороной, а остальные стороны находятся на одной прямой.

При пересечении 2-х прямых получается 4-ре пары смежных углов:

Но, так как ∠1 =∠4, ∠2 = ∠3 (как вертикальные), то достаточно рассматривать

только одну из этих пар.

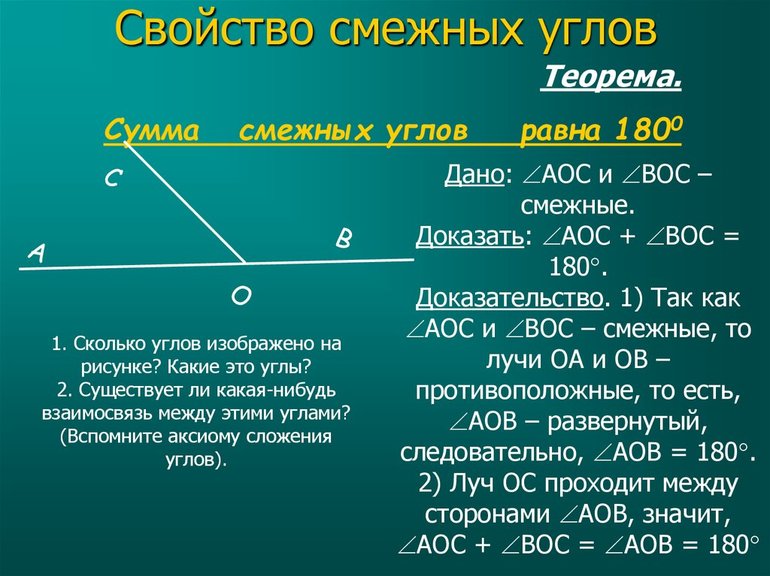
Свойство смежных углов.

Чему равна сумма смежных углов?

Смежные углы равны: сумма смежных углов 180º.

Следствия из теоремы о смежных углах.

Тригонометрические соотношения.

противоположные знаки (исключение неопределенные значения).

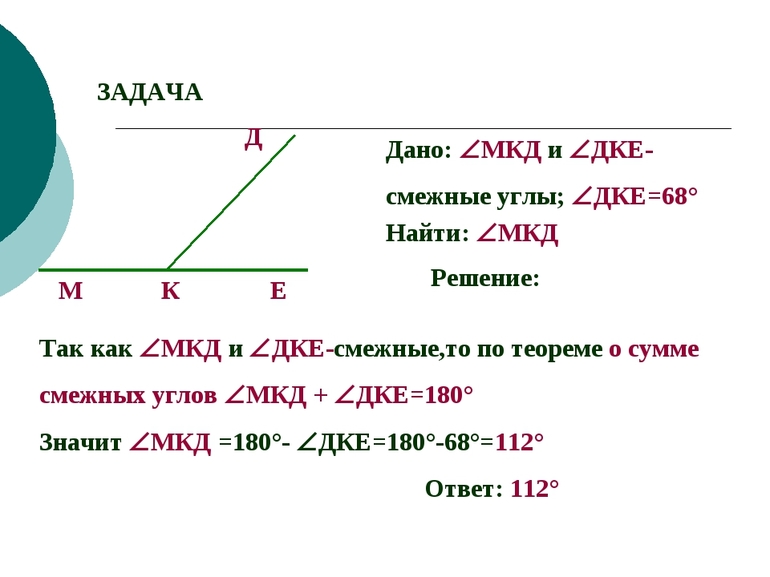
Задание. Чему будет равна градусная мера угла α, когда градусная мера смежного ему угла = 70°?

Как найти смежный угол?

Решение. Из теоремы о смежных углах находим:

Источник

Углы. Смежные углы.

Какие углы называются смежными?

Смежными углами называется пара углов с общей вершиной и одной

общей стороной. 2 оставшиеся стороны делают продолжение друг

другу, образовывая прямую линию. Для угла 135 градусов смежным

будет угол равный 45 градусам. Для угла x градусов смежным

является угол (180 – x) градусов.

Два смежных угла — это углы, с одной общей стороной, а остальные стороны находятся на одной прямой.

При пересечении 2-х прямых получается 4-ре пары смежных углов:

Но, так как ∠1 =∠4, ∠2 = ∠3 (как вертикальные), то достаточно рассматривать

только одну из этих пар.

Свойство смежных углов.

Чему равна сумма смежных углов?

Смежные углы равны: сумма смежных углов 180º.

Следствия из теоремы о смежных углах.

Тригонометрические соотношения.

противоположные знаки (исключение неопределенные значения).

Задание. Чему будет равна градусная мера угла α, когда градусная мера смежного ему угла = 70°?

Как найти смежный угол?

Решение. Из теоремы о смежных углах находим:

Источник

Геометрия. 7 класс

Конспект урока

Смежные и вертикальные углы. Аксиомы и теоремы

Перечень вопросов, рассматриваемых в теме:

Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.

Свойства смежных углов:

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Свойство вертикальных углов: вертикальные углы равны.

Аксиома– положение, принимаемое без доказательств.

Теоретический материал для самостоятельного изучения

Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это смежные углы. На основании этого сформулируем определение смежных углов.

Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.

Давайте докажем это свойство.

Укажем ещё одно свойство смежных углов.

Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.

Углы, которые не являются смежными:

∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.

Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов

Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.

На предыдущих уроках вы познакомились с понятием аксиомы.

В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Используя чертёж, найдите угол ∠ВОК.

№2. Тип задания: единичный / множественный выбор.

Используя чертёж, найдите угол ∠AOD.

№3. Тип задания: выделение цветом.

Выделите верный ответ из списка:

60 0 ; 30 0 ; 75 0 ; 90 0

Источник

Смежные углы

Что такое смежные углы? Какие у них свойства?

Определение.

Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.

∠1 и ∠2 — смежные углы

Сколько смежных углов образуется при пересечении двух прямых?

При пересечении двух прямых образуется четыре пары смежных углов:

Но, так как ∠1 =∠4, ∠2=∠3 (как вертикальные), то достаточно рассмотреть только одну из этих пар.

Свойство смежных углов.

Сумма смежных углов равна 180º.

1) Даны два смежных угла. Один на 42 градуса больше другого. Найти эти углы.

∠AOC и ∠BOC — смежные,

∠AOC на 42º больше, чем ∠BOC

Пусть ∠BOC=хº, тогда ∠AOC= х+42º. Так как сумма смежных углов равна 180º, то ∠BOC+∠AOC=180º.

Значит, ∠BOC= 69º, ∠AOC=69+42=111º.

2) Найти смежные углы, если их градусные меры относятся как 4:5.

Значит, смежные углы равны 4∙20=80º и 5∙20=100º.

3) Один из углов, образованных при пересечении двух прямых, в 5 раз больше другого. Найти эти углы.

Дано: AB и CD — прямые, O — точка их пересечения,

∠AOD в 5 раз больше, чем ∠BOD

При пересечении двух прямых образуются смежные и вертикальные углы. Так как вертикальные углы равны между собой, то углы∠AOD и ∠BOD — смежные. Пусть ∠BOD=xº, тогда ∠AOD=5xº. Так как сумма смежных углов равна 180º, ∠AOD +∠BOD=180º.

Значит, ∠BOD=30º, ∠AOD=5∙30=150º.

Могут ли смежные углы быть равными?

Да. Если смежные углы равны между собой, то, так как сумма смежных углов равна 180º, каждый из них равен половине суммы, то есть 90º.

угол, смежный с прямым, есть прямой угол.

Могут ли два смежных угла быть тупыми? Острыми?

Нет. Так как градусная мера тупого угла больше 90º, то сумма двух тупых углов больше 180º. А сумма смежных углов равна 180º.

Градусная мера острого угла меньше 90º. Значит, сумма двух острых углов меньше 180º.

Таким образом, в паре смежных углов один — тупой, другой — острый (или оба прямые).

Источник

Общие сведения

Основными элементами, используемыми в геометрии, являются лучи и углы. С их помощью образуется любая геометрическая фигура — квадрат, треугольник или любого вида многоугольник. Луч — это полупрямая, то есть часть линии, на которой точки располагаются по одной стороне от зафиксированной. По-другому можно сказать, что луч — это линия, ограниченная только с одной стороны. Обозначают его как прописными латинскими буквами, так и заглавными с названием точек. Во втором случае первой указывается начальная точка.

Два луча, выходящие из одной точки, образовывают угол. По сути, это незамкнутая геометрическая фигура. Она имеет вершину (общую точку) и стороны. Обозначают его с помощью трёх заглавных букв, соответствующих трём точкам — вершине и двум лежащим на разных сторонах лучах. Внутренняя часть формируется из множества точек, принадлежащих плоскости, ограниченной сторонами угла.

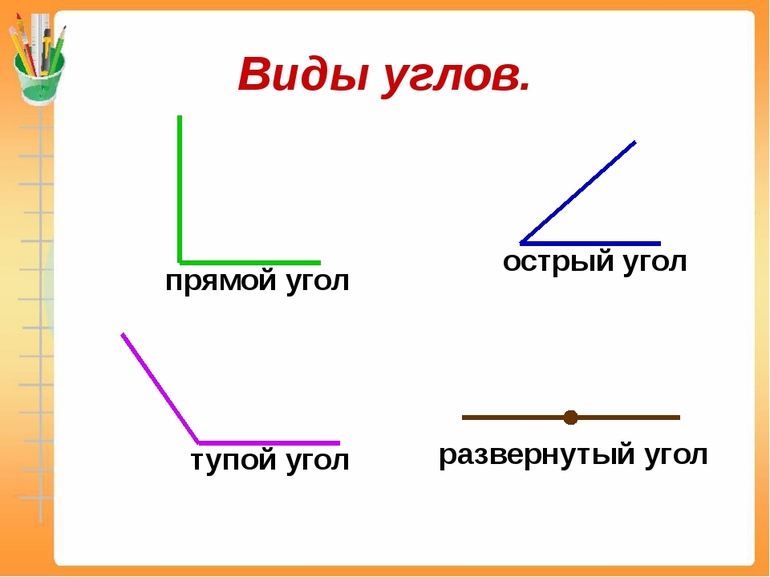
Существует шесть видов углов:

Располагаясь на плоскости, по отношению друг к другу углы могут быть смежными или вертикальными. Согласно определению, смежными углами называют такую пару, у которой одна сторона принадлежит обеим фигурам, а два других луча образуют прямую линию. Вертикальными же считаются углы, стороны которых дополняют друг друга до прямых линий. Они всегда градусно равны.

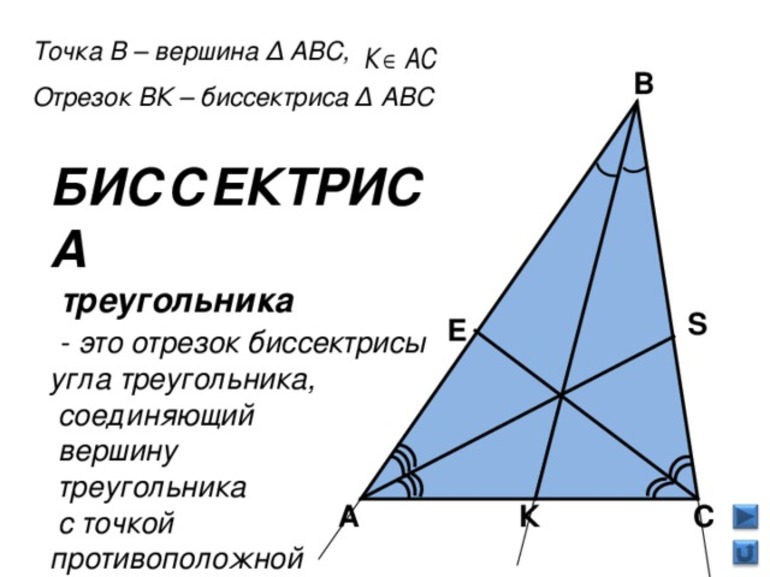
Из угла всегда можно провести линию, делящую его на две равные части. Такой луч, исходящий из вершины, называют биссектрисой. А это значит, что после его проведения образуется два равных смежных угла, обладающих одинаковыми свойствами.

Единицей измерения разворота фигуры является градусная мера. Если в нём содержится нецелое количество градусов, то используются минуты и секунды. Так, в одном градусе содержится 60 минут, а в одной минуте 60 секунд.

Основные факты

Вычисление элементов треугольников используется в географии, строительстве, астрономии, мореплавании и других науках и технике, например, кинематике, механике, оптике, при проведении гармонического анализа. Для успешного решения задач по теме нужно знать следующие факты:

Кроме этого, нужно учесть, что отличие смежных углов от вертикальных заключается в том, что сумма первых равняется 180 градусам, а вторые всегда равняются друг другу.

Иными словами, для пары углов смежным будет угловой элемент, равный у = (180 — x) градусам. Причём при пересечении двух лучей получается четыре смежные пары, из которых две будут вертикальными. Это основополагающие факты, на которых построена геометрия и тригонометрия. Зная их, можно переходить к изучению таких сложных наук, как, например, планиметрия и стереометрия.

Свойства и теорема

С теоремой о смежных углах знакомят на уроках геометрии в седьмом классе средней школы. Исходя из того, что такие фигуры имеют общую вершину и сторону, можно предположить, что сумма углов будет равняться 180 градусам. При этом каждый из них способен дополнить другой до развёрнутого. Равенство суммы 180 градусам и является основной теоремой.

На основании рассмотренной теоремы вытекают три свойства смежных углов:

А также существуют следствия или, как их ещё называют, тригонометрические соотношения. В их основе лежит то, что косинусы и тангенсы рассматриваемых фигур всегда будут равны по величине, но противоположны по знаку. При этом если необходимо построить угол, смежный с существующим, то нужно одну из сторон продлить за вершину.

Указанные свойства используются и при определении подобия треугольников. Например, согласно первому признаку, если два угла равностороннего или разностороннего треугольника совпадают с двумя углами другого, то они подобны. Случается, что по одну сторону от линии могут находиться несколько лучей, имеющих общую вершину. Изобразив такую ситуацию на чертеже, легко убедиться, что если все полученные углы сложить, то их сумма будет соответствовать значению двух прямых, а также из них всегда можно образовать смежную пару.

Этот свойство используется тогда, когда необходимо определить, чему равняется сумма углов вокруг конкретно взятой вершины. То есть продолжив одну из сторон за рассматриваемую вершину, можно получить две группы: первую — сумма которых равна двум прямым, и вторую — сумма которых также равна двум прямым углам. Отсюда следует, что сумма вокруг общей вершины будет равняться прямым углам.

Примеры решения задач

Решать задачи по заданной теме проще, если выполнять чертежи. С их помощью, а также зная свойства и теоремы, найти правильный ответ не составит особого труда. Существуют типовые задания, позволяющие закрепить пройденный материал и на практике применить полученные знания. Вот наиболее интересные из них с подобным решением:

Уметь правильно решать задачи важно, так как в дальнейшем эти знания помогают находить такие важные элементы, как площадь треугольника, зная только разворот и высоту произвольной фигуры, а далее уже легко будет вычислить и объём. Кроме этого, правила смежности часто используются в тригонометрии при нахождении синусов и косинусов.

Вычисление на онлайн-калькуляторе

Нахождение градусной меры смежных элементов обычно не вызывает проблем и относится к элементарным действиям при исследованиях различных треугольников, например, остроугольных или равнобедренных. Но при работе с нецелыми числами или в процессе обучения имеет смысл использовать так называемые онлайн-калькуляторы.

Это обычные интернет-сайты, содержащие встроенную программу для автоматических расчётов. Пользоваться ими сможет каждый, кто имеет компьютер или гаджет с установленным веб-обозревателем. Вся работа с сервисом сводится к загрузке его интернет-страницы и заполнения специальной формы, в которую вводятся исходные данные. Затем нажимается интерактивная кнопка и на дисплее появляется ответ.

Вычисление обычно занимает пару секунд, а появление ошибки исключено. Кроме этого, на сайтах, предлагающего такого рода услуги, содержится весь необходимый для расчётов теоретический материал. Поэтому даже слабо подготовленный по теме пользователь сможет понять, откуда и каким образом получился тот или иной ответ.

Из множества сервисов, существующих в русскоязычном сегменте всемирной сети, можно выделить следующие:

Эти сервисы доступны бесплатно, имеют интуитивно понятный интерфейс на русском языке.

При этом пользователям предлагается ознакомиться с развёрнутым решением, то есть указан поэтапный расчёт. Для удобства на страницах даётся не только необходимая теория, но и ряд типовых примеров с подробным описанием действий.

Следует отметить, что указанные сервисы могут находить ответ для любой сложности математической задачи. Особенно востребованными становятся такие вычисления в инженерии, связанные с тригонометрическими функциями. Ведь для таких расчётов важны точность и время, что вполне могут обеспечить онлайн-калькуляторы.

Источник