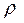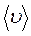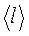Какие явления относятся к явлению переноса что общего в этих явлениях

К явлениям переноса относятся

Явления переноса в газах

Явлениями переноса называются процессы выравнивания массы, импульса, энергии, электрического заряда и т. д.

· диффузия(обусловленная переносом массы);

· теплопроводность (обусловленная переносом энергии);

· внутреннее трение или вязкость (обусловленная переносом импульса).

Диффузияв газе–это процесс перемешивания молекул, сопровождающийся переносом массы из мест с большей концентрацией (плотностью) данных молекул в места с меньшей концентрацией этих молекул.Таким образом, в процессе диффузии переносится масса, а изменяющейся величиной является плотность газа r.

Явление диффузии для химически однородного газа подчиняется закону Фика:

, (18)

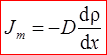
где 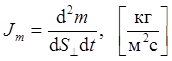– плотность потока массы –величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси x;

D – коэффициент диффузии,[м 2 /с];

— градиент плотности, [кг/м 4 ], равный изменению плотности на единицу длиныхв направлении нормали к этой площадке.

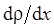
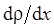
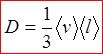
Знак «минус» показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки J_m и противоположны). Коэффициент диффузии D численно равен плотности потока массы при единичном градиенте плотности. Согласно кинетической теории газов

. (19)

Теплопроводность –это процесс выравнивания температуры газа, сопровождающийся направленным переносом тепла из более нагретых мест в менее нагретые.

Перенос энергии в форме теплоты подчиняется закону Фурье:

, (20)

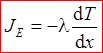
где 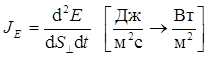– плотность теплового потока –величина, определяемая энергией, переносимой в единицу времени через единичную площадку, перпендикулярную оси x;

Знак «минус» показывает, что при теплопроводности тепловая энергия переносится в направлении убывания температуры. Коэффициент теплопроводностиl численно равен плотности теплового потока при единичном градиенте температуры.

Согласно кинетической теории газов

, (21)

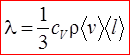
Внутреннее трение (вязкость) –это возникновение сил трения между слоями газа или жидкости, перемещающимися парал-лельно друг другу с различными скоростями.

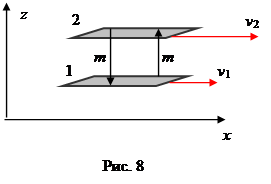Явление вязкости сопровождается пере-носом импульса направленного движения из более быстрых слоев в более медлен-ные в направлении z, перпендикулярном направлению x движения слов газа.

Сила внутреннего трения описывается законом Ньютона:

, (22)

— градиент скорости, 1/c;

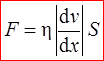
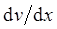
S – площадь, на которую действует сила F.

Закон Ньютона можно представить в виде

, (23)

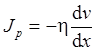
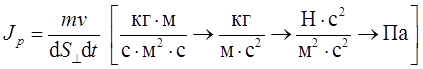
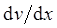
где – плотность потока импульса –величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси x через единичную площадку, перпендикулярную этой оси;

— градиент скорости.

Знак «минус» указывает, что импульс переносится в направлении убывания скорости.

Динамическая вязкость h численно равна плотности потока импульса при единичном градиенте скорости. Она вычисляется по формуле

. (7.40)

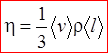
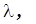
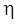
Все явления переноса сходны между собой. Зависимости между Dи :

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Явления переноса

Явления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества.

Выравнивание неоднородностей приводит к возникновению явлений переноса. К этим явлениям относятся диффузия, вязкость и теплопроводность.

Явление переноса заключается в том, что возникает упорядоченный перенос массы (диффузия), импульса (вязкость) и внутренней энергии (теплопроводность). При этом нарушается полная хаотичность движения молекул и максвелловское распределение молекул по скоростям.

Микроскопические процессы в статистически неравновесных системах исследуются методами физической кинетики. Она изучает процессы установления равновесия в системах, первоначально находившихся в неравновесном состоянии. Физическая кинетика исходит из представлений о молекулярном строении рассматриваемых сред и силах взаимодействия между составляющими их молекулами. Это дает возможность рассчитать кинетические коэффициенты процессов.

Время релаксации.Рассмотрим случай, когда замкнутая макроскопическая система в начальный момент находится не в равновесном состоянии. а в одном из маловероятных состояний. Это может произойти в результате какого-либо внешнего воздействия, которое затем устраняется и система становится замкнутой. Примером может служить газ, неравномерно распределенный внутри сосуда. По истечении некоторого времени, которое называется временем релаксации t, система, которая первоначально находилась в неравновесном, маловероятном состоянии, переходит в наиболее вероятное, равновесное состояние. Протекающие при этом в системе процессы зависят от природы системы и характера отклонения ее от равновесного состояния.

Время, в течение которого система достигает равновесного состояния, называется временем релаксации.

Это время может составлять как доли секунды, так и столетия, в зависимости от вида взаимодействия между частицами системы и от частоты переходов между различными доступными состояниями системы.

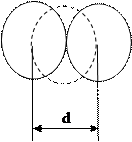
Эффективное сечение рассеяния. Поскольку молекулы газа движутся беспорядочно, вследствие этого они должны случайным образом сталкиваться друг с другом, отклоняясь от направления своего движения. Две молекулы могут столкнуться (упруго или не упруго), если расстояние между их центрами будет меньше их диаметра d (рис.1.9.1).

Каждое столкновение происходит после прохождения молекулой средней длины свободного пробега l. В соответствие с этим вводят понятие эффективного сечения рассеяния s=pd 2 (площадь круга диаметром d). Это основная характеристика вероятности возникновения определенного конечного состояния двух сталкивающихся частиц.

Длина свободного пробега и эффективное сечение связаны между собой соотношением

Эффективное сечение зависит от скорости молекул, а значит от температуры. Следует заметить, что, вообще говоря, эффективное сечение имеет чисто геометрический смысл, а является вероятностной характеристикой процесса. Большая величина эффективного сечения не обусловлена большими размерами молекулы, однако, определяет большую вероятность столкновения.

Диффузия представляет собой перенос молекул вещества в направлении уменьшения концентрации частиц. Если концентрации вещества изменяется по координате x, оставаясь постоянной по двум другим, тогда нестационарный процесс выравнивания концентраций, описывается законом Фика:

,

,

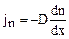
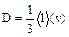
Диффузия имеет место, как в газах, так и в жидкостях и твердых телах. Однако коэффициент диффузии в этой последовательности резко уменьшается.

Теплопроводность проявляется при наличии разности температур и представляет собой направленный перенос тепла от более нагретых частей газа к менее нагретым (посредством столкновения молекул), приводящий к выравниванию температур.

Будем считать, что изменение (градиент) температуры имеет место по одной координате х. Тогда перемещение тепла между стенками осуществляется последовательным переносом тепла от одного слоя газа к другому.

Поток тепловой энергии через единицу площади, или плотность теплового потока пропорционален градиенту температуры с обратным знаком (закон Фурье)

,

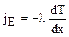
Коэффициент теплопроводности численно равен потоку тепла при градиенте температуры равном единице [1K/м]. В технике его иногда выражают в [кДж/(м€час€град)].

Молекулярно-кинетический расчет коэффициента теплопроводности приводит к результату

,

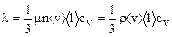
с_v— удельная теплоемкость при постоянном объеме;

Связь l с концентрацией и длиной свободного пробега показывает, что коэффициент теплопроводности газов не зависит от давления. Молекулы легких газов имеют большую среднюю скорость и, соответственно, больший коэффициент теплопроводности. Это подтверждают эксперименты и применяется на практике.

Наряду с коэффициентом теплопроводности на практике используется также коэффициент температуропроводности

.

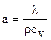
Размерность коэффициента температуропроводности [м 2 /с] и его величина совпадают с коэффициентом диффузии D. Он представляет собой коэффициент «диффузии температуры». Если коэффициент теплопроводности характеризует способность среды проводить тепло. то коэффициент температуропроводности служит мерой теплоинерционных свойст вещества. Другими словами, скорость изменения температуры во времени dT/dt в любой точке пространства пропорциональна а. выравнивание температуры быстрее происходит там. где больше а. Величина коэффициента температуропроводности зависит от природы вещещства. Например, газы и жидкости имеют большую теплоинерционность и, значит, малый коэффициент температуропроводности. Металлы, имея малую тепловую инерцию, обладают большим коэффициентом температуропроводности.

В нестационарных явлениях тепло и массопереноса (диффузия и теплопроводность между двумя сосудами или между объектом и средой) важной характеристикой служит время установления равновесия. Вследствие этого вводится в качестве параметра процесса время релаксации (постоянная времени) t. Это время. за которое разность концентраций или температур уменьшится в е раз. Величина t связана с кинетическими параметрами вещества (l, D, с_р, r) и геометрическими характеристиками объектов.

Вязкостью называют силу трения между слоями газа или жидкости, движущимися друг относительно друга параллельно с различными скоростями, что приводит к переносу импульса в перпендикулярном к скорости направлении

,

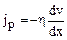
где j_p— напряжение трения или плотность потока импульса;

С физической точки зрения динамическая вязкость численно равна импульсу, переносимому в единицу времени через плоскость 1м 2 при градиенте скорости в направлении перпендикулярном плоскости равном единице (1м/с на 1м длины).

При молекулярно-кинетическом рассмотрении динамическая вязкость принимает вид

.

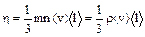
Из этого выражения следует, что динамическая вязкость газов не зависит от давления и возрастает с повышением температуры. Вязкость жидкостей с повышением температуры уменьшается. Эксперименты подтверждают такие выводы.

Кроме динамической вязкости используется также кинематическая вязкость n:

Она имеет такую же размерность, как и коэффициент диффузии и численно ему равна. В соответствие с этим кинематическую вязкость можно назвать коэффициентом диффузии скорости.

Источник

Явления переноса (диффузия, теплопроводность, вязкость)

В неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос массы, энергии, импульса.

Диффузия обусловлена переносом массы, теплопроводность – переносом энергии, а вязкость – переносом импульса.

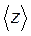
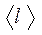
Для характеристики необратимых процессов переноса вводятся параметры теплового движения молекул: среднее число соударений молекулы в единицу времени и средняя длина свободного пробега молекул .

Среднее число соударений молекулы за 1 с : ,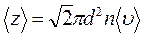

где d – эффективный диаметр молекул, т.е. минимальное расстояние, на которое сближаются при столкновении центры двух молекул,

– эффективное сечение молекул, – концентрация молекул,

– средняя арифметическая скорость молекул.

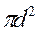
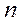
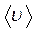
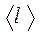
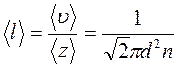
Средняя длина свободного пробега молекул , т.е. средний путь, проходимый молекулой между двумя последовательными столкновениями:

.

При рассмотрении одномерных явлений переноса система отсчета выбирается так, чтобы ось х была ориентирована в направлении переноса.

1. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное взаимопроникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел. Диффузия сводится к переносу массы, возникает и продолжается до тех пор, пока на границе соприкосновения двух сред градиент плотности отличен от нуля.

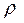
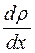
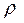
Градиент плотности вдоль выбранной оси х, перпендикулярной плоскости соприкосновения двух сред, обозначается как и показывает как быстро изменяется величина плотности от точки к точке вдоль оси х.

Количественно явление диффузии подчиняется закону Фика:

,

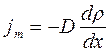
где 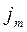– плотность потока массы, то есть величина, определяемая массой газа, диффундирующего через единичную площадку S в единицу времени,

D – коэффициент диффузии.

Знак минус в приведенной формуле означает, что перенос массы происходит в направлении убывания плотности.

Согласно молекулярно-кинетической теории идеального газа, коэффициент диффузии D: ,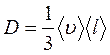

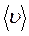
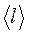
где – средняя скорость теплового движения молекул,

– средняя длина свободного пробега молекул.

2. Теплопроводность. Если в одной области газа температура больше,чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, то есть процесс выравнивания температуры. Этот процесс переноса энергии, называемый теплопроводностью, возникает и продолжается до тех пор, пока на границе соприкосновения двух частей газа градиент температуры отличен от нуля.

Градиент температуры Т газа вдоль выбранной оси х, перпендикулярной плоскости соприкосновения двух частей газа, имеющих различную температуру, обозначается как 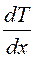и показывает как быстро изменяется температура газа от точки к точке вдоль оси х.

Количественно теплопроводность подчиняется закону Фурье:

,

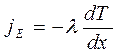
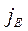
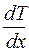
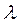
где– плотность теплового потока, определяемая энергией, переносимой в форме теплоты через единичную площадку S в единицу времени,

– градиент температуры в направлении x, перпендикулярном выбранной площадке S,

– коэффициент теплопроводности.

Знак минус в приведенной формуле означает, что при теплопроводности энергия переносится в направлении убывания температуры.

Согласно молекулярно-кинетической теории идеального газа, коэффициент теплопроводности: ,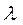

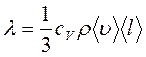
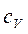
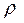
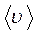
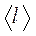
где – удельная теплоемкость газа при изохорном процессе (количество теплоты, необходимое для изохорного нагревания 1 кг газа на 1 К),

– плотность газа,

– средняя скорость теплового движения молекул,

– средняя длина свободного пробега молекул.

3. Вязкость. Вязкость это свойство жидкости или газа, обусловленное внутренним трением между соприкасающимися параллельными слоями жидкости или газа, движущимися с различными скоростями. В результате, импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Другими словами, внутреннее трение приводит к переносу импульса от одного движущегося слоя жидкости или газа к другому соприкасающемуся с ним слою.

Количественно сила внутреннего трения между двумя соприкасающимися слоями жидкости или газа подчиняется закону Ньютона:

,

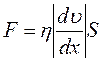
где h – коэффициент динамической вязкости,

– градиент скорости, показывающий быстроту изменения скорости течения жидкости или газа от слоя к слою в направлении х, перпендикулярном направлению движения слоев,

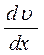
S – площадь соприкосновения слоев жидкости или газа, на которые действует сила внутреннего трения F.

Закон Ньютона для внутреннего трения можно представить в виде:

,

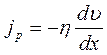
где 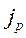– плотность потока импульса – величина, определяемая импульсом, переносимым в единицу времени через единичную площадку S соприкосновения слоев жидкости или газа в направлении оси х, перпендикулярном направлению движения слоев жидкости или газа.

Знак минус в приведенной формуле означает, что импульс переносится от слоя к слою жидкости (газа) в направлении убывания скорости их движения.

Согласно молекулярно-кинетической теории идеального газа, коэффициент динамической вязкости идеального газа h определяется следующим образом:

,

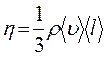
где – плотность газа,

– средняя скорость теплового движения молекул,

– средняя длина свободного пробега молекул.

Источник