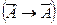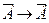Какова логическая структура теоремы и что значит доказать теорему

Лекция №5. Математические предложения и методика изучения теорем

1.Виды математических предложений

2.Логическая структура теорем. Виды теорем и связь между ними

3.Необходимые и достаточные условия, теоремы – свойства и теоремы – признаки

4.Методика обучения доказательству

I.Каждая математическая теория представляет собой множество предложений, описывающих структуру этой теории. С каждым математическим предложением связаны содержание (выраженное в нем математическое содержание) и логическая форма (или структура). В математике различают элементарные и составные предложения. Составные предложения образуются из элементарных с помощью логических связок “не”, “и”, “или”, “если …, то”, “тогда и только тогда”, “для всякого”, обозначающих логические операции.

Выявить логическую структуру составного предложения – значит установить:

1) Из каких элементарных предложений образовано данное составное предложение;

2) С помощью каких логических связано.

а)“ 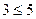” б) “ ”

Это сложное предложение:

а) 1) 2) а) 1) 2)

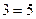
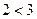
б) или (дизъюнкция) б) и (конъюнкция)

К математическим предложениям относятся:

· Теорема – математическое предложение, истинность которого доказывается,

· Аксиома– математическое предложение, истинность которого принимается без доказательства,

· Определения математических понятий.

Среди суждений, устанавливающих различные отношения между математическими понятиями, выделяют высказывания и высказывательные формы.

Определение. Высказываниемназывается предложение, относительно которого имеет смысл вопрос, истинно оно или ложно.

— ложное высказывание.

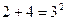
Определение. Высказывательная форма – это предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке в него конкретных значений переменных.

— одноместная высказывательная форма

— двуместная высказывательная форма

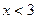
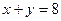
II.Каждая теорема состоит из 3 частей:

В разъяснительной части описывается, какие точки или фигуры рассматриваются в теореме. Для словесного выражения теорем обычно используют две формы суждений: категоричную, условную (импликативную).

Категоричная – когда принадлежность или непринадлежность некоторого признака предмету независимо от каких бы то ни было условий.

Условная – когда истинность суждения ставится в зависимости от определенных условий.

Если теорема содержит несколько условий и заключений, то теорема сложная.

Логико – математический анализ теоремы предполагает:

1) установление формы суждения;

2) выделение разъяснительной части, условия, заключений;

3) установление факта, какая дана теорема – простая или сложная.

— прямая теорема

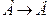
Если разъяснительную часть оставить без изменения, а условие и заключение поменять местами, то получим утверждение обратное данному. ( )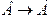

Если разъяснительную часть оставить без изменения, а условие и заключение утверждения заменить их отрицанием, то получим утверждение противоположное данному.

Если оставить без изменения разъяснительную часть и поменять местами условие и заключение утверждения, противоположного данному, то получим утверждение, обратное противоположному.

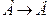
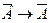
Утверждения , всегда одновременно истинны или ложны. Эта связь между теоремами используется при доказательстве методом от противного. Если первую теорему трудно доказать, то её заменяем на обратную противоположной.

Схема метода доказательства от противного:

1) предлагаем противоположное тому, что требуется доказать, т.е. …

2) из предложения следует, что …

3) получаем противоречие с …

4) значит наше предположение неверно, а верно то, что требовалось доказать, т.е …

III.Если из предложения следует предложение , то говорят, что — достаточное условие для , а — необходимое условие для .

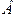
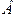
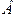
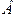
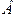
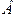
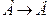
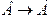
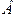
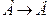
Другими словами, предложение называется необходимым условием для , если оно логически следует из . Предложение называется достаточным условием для ,если из него следует.

Если “и”, “и”, то говорят, что является необходимым и достаточным условием для , и наоборот.

Пример: Если число делится на 10, то оно делится на 2.

истинно, т.е. — достаточное для ,

— необходимое для .

Определение. Под свойствомпонимается обязательное условие принадлежности объекта к данному виду.

Другими словами, свойство – это то, что мы можем получить (или доказать), исходя из того, что объект принадлежит к данному виду.

Например, мы знаем, что 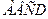— ромб. Следовательно, мы можем утверждать, что:

¾ — четырехугольник

¾ — параллелограмм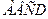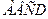

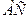
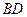
¾ диагонали и перпендикулярны

Все это – свойства ромба. Иначе их называют необходимымиусловиями того, что 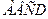— ромб.

Свойство для любого понятия можно сформулировать по следующей схеме:

Если что-то является объектом такого-то вида,

для него выполняется то-то.

Признак –это достаточное условие, т.е. такое, которое формулируется по схеме:

Если для данного объекта выполняется такое-то условие,

объект принадлежит к рассматриваемому виду.

В математике часты случаи, когда одно и то же условие является и свойством, и признаком данного понятия.

Признак: Если в четырёхугольнике диагонали пересекаются в одной точке и делятся ею пополам, то четырёхугольник является параллелограммом.

Свойство: Если четырёхугольник является параллелограммом, то его диагонали пересекаются в одной точке и делятся ею пополам.

Такое условие, которое является одновременно и признаком, и свойством, называется характеристическим свойством понятия. Сформулировать можно его двумя способами с использованием слов: или “необходимо и достаточно”, или “тогда и только тогда”.

1) Четырехугольник является параллелограммом тогда и только тогда, когда его диагонали пересекаются в одной точке и делятся ею пополам.

2) Для того чтобы четырехугольник являлся параллелограммом необходимо и достаточно, чтобы его диагонали пересекались и делились ею пополам.

IV.При изучении теоремы можно условно выделить следующие этапы:

1) подготовительный этап

I. Осуществляется актуализация знаний, необходимых для введения и доказательства теоремы.

¾ мотивация изучения теоремы:

a) обобщение необходимых в жизни фактов и явлений и перевод их на математический язык;

b) показать необходимость знания той или иной теоремы для решения практических задач;

c) показать, как решалась данная проблема в истории науки.

¾ с помощью практической работы подвести к открытию теоремы.

¾ разобраться в структуре теоремы (дано, доказать);

¾ сделать чертеж и краткую запись

III.С помощью специально подобранных заданий и вопросов осуществить:

¾ Решение простейших задач (по готовому чертежу) на непосредственное применение теоремы.

IV. Решение разнообразных задач, повторение доказательства.

1.При поиске путей доказательства следует иметь ввиду:

1) Если в доказательстве используется известный учащимся метод или доказательство осуществляется по известной уже схеме, то учащимся сообщается метод, а дальше беседа по плану:

¾ каков 1-ый шаг данного метода?

¾ Как это сделать для данной теоремы?

2) если теорема содержит небольшое число этапов доказательства, каждый из которых “прозрачно” связан с другим, то применяем аналогичные рассуждения: что нужно знать, чтобы доказать (с конца)

3) если теорема сложная, то ученикам следует сообщить идею доказательства.

2.На этапе усвоения доказательства задаем вопросы:

Источник

Что такое аксиома, теорема и доказательство теоремы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие аксиомы

Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.

Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.

Синоним аксиомы — постулат. Антоним — гипотеза.

Основные аксиомы евклидовой геометрии

Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.

А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.

Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:

Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.

У этой аксиомы два следствия:

Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:

Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.

На картинке можно увидеть, как это выглядит:

Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.

Понятие теоремы

Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.

Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.

Состав теоремы: условие и заключение или следствие.

Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.

Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.

Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.

Примеры следствий из аксиомы о параллельности прямых:

Доказательство теоремы — это процесс обоснования истинности утверждения.

Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.

Способы доказательства геометрических теорем

Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.

Приемы для доказательства в геометрии:

Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.

Прямая и обратная теорема взаимно-обратные. Например:

В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.

Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.

Вот, как выглядит взаимное отношение теорем на примере:

В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.

Записывайся на онлайн обучение по математике для учеников с 1 по 11 классы!

Доказательство через синтез

Рассмотрим пример синтетического способа доказательства.

Теорема: сумма углов треугольника равна двум прямым.

Дан треугольник: ABC. Нужно доказать, что A + B + C = 2d.

Доказательство:

Проведем прямую DE, так чтобы она была параллельна AC.

Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно, α + B + γ = 2d.

Так как α = A, γ = C, то заменим в предыдущем равенстве углы α и γ равными им углами: A + B + C = 2d. Что и требовалось доказать.

Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, которые лежат по одну сторону прямой. Есть связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною. Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.

Доказательство через анализ

Рассмотрим пример аналитического способа доказательства.

Теорема: диагонали параллелограмма пересекаются пополам.

Дан параллелограмм: ABCD.

Доказательство:

Если диагонали пересекаются пополам, то треугольники AOB и DOC равны.

Равенство же треугольников AOB и DOC вытекает из того, что AB = CD, как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ, как накрест-лежащие углы.

Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до уже доказанного предложения.

Теоремы без доказательств

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:

Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:

где a, b и c — стороны плоского треугольника,

α — угол напротив стороны а.

Следствия из теоремы косинусов:

Понятия свойств и признаков

У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.

Свойства и признаки — понятия из обычной жизни, которые мы часто используем.

Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.

Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.

Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.

Признак — это то, по чему мы однозначно распознаем объект.

Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.

А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.

Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.

Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:

Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.

Такие утверждения называют необходимым и достаточным признаком.

Источник

Статья «Изучение и доказательство теорем»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Е.В. Петрова,учитель математики СОШ №25 г. Владимира

Изучение и доказательство теорем.

Реализация современной роли математики предполагает улучшение математической подготовки учащихся, важное место в котором отводится умению открывать закономерности, обосновывать их и применять на практике. Формирование алгоритмического, эвристического, абстрактного мышления учащихся осуществляется также главным образом в процессе доказательства. Обучение математике предполагает обучение способам деятельности по приобретению знаний, что требует выявления и освоения в процессе обучения математике различных схем используемых в математике рассуждений. В опытных науках мы постоянно обращаемся к наблюдениям и экспериментам, чтобы проверить те или иные утверждения. Совершенно иначе дело обстоит в математике. Теорема считается доказанной только в том случае, если она логически выведена из других предложений. Поэтому проблема обучения учащихся доказательству всегда являлась одной из центральных в методике преподавания математики.

В настоящее время, идущий процесс гуманизации образования предполагает направленность обучения на развитие личности, на формирование нравственности, чему способствует обучение доказательству, где важная роль отводится обучению поиска способов доказательства, их сравнения, выбора наиболее простого из них.

Что значит доказать теорему, что такое доказательство?

Когда вы убеждаете своего товарища в чем-либо или отстаиваете в споре с ним свое мнение, свою точку зрения, то вы по существу производите доказательство (умело или неумело — это уже другой вопрос).

Таким образом, при доказательстве теоремы мы сводим ее к ранее доказанным теоремам, а те в свою очередь еще к другим и т.д. Очевидно, что этот процесс сведения должен быть конечным, и поэтому всякое доказательство в конце концов сводит доказываемою теорему к исходным определениям и принятым без доказательства аксиомам.

Процесс доказательства – сложный процесс мышления, и он формируется лишь постепенно, от простых к более сложным структурам. Следовательно, обучение доказательству представляет собой сложную систему, структура которой обусловлена многочисленными связями между различными ее составляющими.

К 13 – 14 годам мозг школьника становится способным овладеть абстрактным, обоснованным, рассуждающим мышлением. Развитие доказательного мышления, отмечает П. П. Блонский, проходит две стадии. В подростковом возрасте школьник скорее усваивает доказательства, чем самостоятельно пользуется ими, и еще меньше он создает их: в этом возрасте доказывание скорее дело памяти. В юношеском же возрасте уже заметно выступают критическое мышление к даваемым доказательствам и стремление к своим доказательствам. Все вышесказанное приводит к выводу о необходимости исследования индивидуальных познавательных стратегий школьников при изучении и доказательстве теорем.

Над этой проблемой я работаю первый год. Сначала я определила цель, задачи и гипотезу исследования.

Цель: выявить и развить индивидуальные стратегии изучения и доказательства теоремы в 8 классе.

1. Выявить индивидуальные стратегии изучения и доказательства теорем на основе вопросника (с элементами листа анализа).

2. Развить индивидуальные стратегии учащихся через обсуждение полученных результатов, создание банка успешных действий при выполнении изучения и доказательства теорем.

3. Разработать советы по успешному изучению теорем по геометрии.

4. Проанализировать результаты освоения учащимися теорем до и после применения технологии ЦРПС, разработать и апробировать памятку успешной деятельности учеников.

Гипотеза: осмысление учащимися собственных действий при изучении теорем позволит развить навыки доказательстваирешения задач по геометрии, достичь более высоких результатов обучения.

Под обучением доказательству надо понимать обучение учащихся анализу готовых доказательств, их воспроизведению, самостоятельному открытию фактов, поиску других путей доказательств, а также опровержению выдвинутых предложений.

Свой эксперимент я начала с вопроса, на который получила неожиданный ответ.

На первом этапе учащимся было предложено описать действия, которые они совершают при знакомстве и доказательстве теоремы. В результате были получены следующие варианты:

Источник