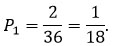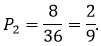Какова вероятность что на кубике выпадет 6
Решение задач о бросании игральных костей
Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.
Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).
Одна игральная кость
Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?
Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.
Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.
Две игральные кости
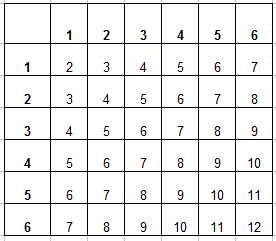
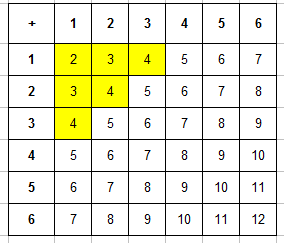
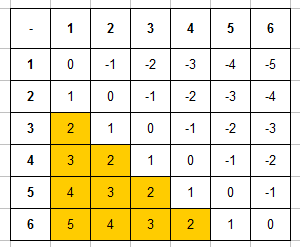
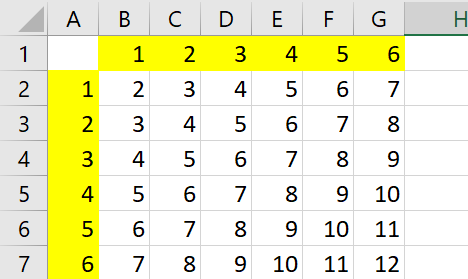
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:
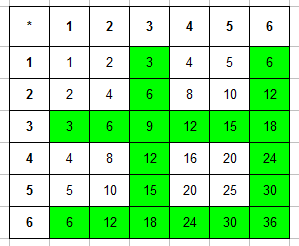
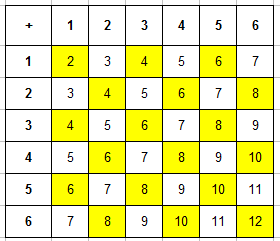
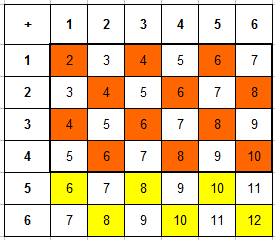
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:
Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).
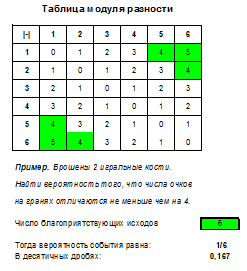
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.
Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).
Другие задачи про кости и кубики
Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.
Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.
В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.
Теперь подберем такие исходы, которые дают в сумме 15 очков.
Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.
Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.
В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.
Приведем еще пример, решаемый аналогичным образом.
Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.
Полезные ссылки
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.
В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.
Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.
Еще по теории вероятностей:
В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):
Игральные кости и математика. Наиболее вероятные комбинации.
Всем добрый вечер, сегодня поговорим о том, какие очки на костях наиболее вероятны. Запасайтесь чайками и печеньем, погнали!
Почему же? А давайте сначала помоделируем, а потом докажем.
Как видим, очень много раз выпала семерка, а вот 12 получается только в одном случае. Доказать это можно так:
Ну и напоследок для 3-5 костей:
Спасибо всем за прочтение!
Автор любит открывать очевидный взгляд на очевидные вещи!
А с какой вероятностью выпадает 7 на одном кубике?
там 6 во 2 и 3 случае вместо 5
Простенькая программа, моделирующая вероятности для разного количества костей (DEPTH)
DEPTH = 7
r = [0 for i in range(1 + 5 * DEPTH)]
def go(s, d=2):
if d == 0:
r[s] += 1
else:
for i in range(6):
go(i + s, d-1)
go(0, DEPTH)
for i, h in enumerate(r):
s = str(i + DEPTH) + «: »
print(s + » » * (6-len(s)) +»P
Roll Player
Можно выбрать одну из 6 рас, некоторые из которых обладают бонусами либо штрафами к своим характеристикам. (Например, эльфы имеют бонус к ловкости “+2” и штраф к телосложению “-2”.)
Перед началом игры участники случайном образом определяют класс, мировоззрение и историю своих героев.
Мировоззрение указывает на характер и отношение героя к окружающему миру его обитателям.
По ходу игры специальный маркер будет перемещаться по ячейкам этой карты, а его положение в конце игровой сессии может повлиять на финальный счёт.
История персонажа проливает свет на тайны из его прошлой жизни. Располагать кубики в ячейках планшетов желательно так, чтобы цвета некоторых из них совпадали с цветовой схемой карты истории персонажа. Это даёт бонусные очки.
Дополнительное развитие героя осуществляется за счёт карт навыков, черт характера, оружия и брони.
Эти карты приобретаются в процессе игры и располагаются по обе стороны и снизу планшета:
Каждый ход на протяжении всей игры кубики не глядя тянутся из мешочка и кладутся в ячейки планшетов каждого из игроков. При помещении нового кубика в ячейку открывается возможность произвести определённые действия с имеющимися кубиками:
— изменить значение кубика, перевернув его нижней гранью к верху;
— поменять два кубика местами;
— изменить значение кубика, увеличив или уменьшив его на “1”;
— взять жетон красноречия, дающего скидку при покупке карт в текущем раунде.
Игра заканчивается, когда игроки заполняют все ячейки на своих планшетах. После чего происходит подсчёт очков репутации. Набравший большее количество очков объявляется победителем!
Незамысловатый и вместе с тем увлекательный игровой процесс сделал возможным выпуск дополнения Roll Player: Monsters & Minions. Здесь игрокам всё же дают шанс испытать своих героев в деле и сразиться со всевозможными чудовищами.
Вероятность игральной кости.
Задачи на вероятность игральной кости не менее популярны, чем задачи о подбрасывании монет. Условие такой задачи обычно звучит так: при бросании одной или нескольких игральных костей (2 или 3), какова вероятность того, что сумма очков будет равна 10, или число очков равно 4, или произведение числа очков, или делится на 2 произведение числа очков и так далее.
Применение формулы классической вероятности является основным методом решения задач такого типа.
Одна игральная кость, вероятность.
Задача 1. Один раз брошена игральная кость. Какова вероятность выпадения четного числа очков?
Поскольку игральная кость собой представляет кубик (или его еще называют правильной игральной костью, на все грани кубик выпадет с одинаковой вероятностью, так как он сбалансированный), у кубика 6 граней (число очков от 1 до 6, которые обычно обозначаются точками), это значит, что в задаче общее число исходов: n=6. Событию благоприятствуют только исходы, при которых выпадает грань с четными очками 2,4 и 6, у кубика таких граней: m=3. Теперь можем определить искомую вероятность игральной кости: P=3/6=1/2=0.5.
Задача 2. Брошен один раз игральный кубик. Какова вероятность, что выпадет не менее 5 очков?
Решается такая задача по аналогии с примером, указанным выше. При бросании игрального кубика общее число равновозможных исходов равно: n=6, а удовлетворяют условие задачи (выпало не менее 5 очков, то есть выпало 5 или 6 очков) только 2 исхода, значит m=2. Далее находим нужную вероятность: P=2/6=1/3=0.333.
Две игральные кости, вероятность.
Задача 3. Брошены одновременно 2 игральные кости. Какова вероятность выпадения суммы менее 5 очков?
Теперь можно заполнить таблицу, для этого в каждую ячейку заносится число суммы очков, которые выпали на первой и второй кости. Заполненная таблица выглядит так:
Благодаря таблице определим число исходов, которые благоприятствуют событию » выпадет в сумме менее 5 очков». Произведем подсчет числа ячеек, значение суммы в которых будет меньше числа 5 (это 2, 3 и 4). Такие ячейки для удобства закрашиваем, их будет m=6:
Учитывая данные таблицы, вероятность игральной кости равняется: P=6/36=1/6.
Задача 4. Было брошено две игральные кости. Определить вероятность того, что произведение числа очков будет делиться на 3.
Для решения задачи составим таблицу произведений очков, которые выпали на первой и на второй кости. В ней сразу же выделим числа кратные 3:
Записываем общее число исходов эксперимента n=36 (рассуждения такие же как в предыдущей задаче) и число благоприятствующих исходов (число ячеек, которые закрашены в таблице) m=20. Вероятность события равняется: P=20/36=5/9.
Задача 5. Дважды брошена игральная кость. Какова вероятность, что на первой и второй кости разность числа очков будет равна от 2 до 5?
Чтобы определить вероятность игральной кости запишем таблицу разностей очков и выделим в ней те ячейки, значение разности в которых будет между 2 и 5:
Число благоприятствующих исходов (число ячеек, закрашенных в таблице) равно m=10, общее число равновозможных элементарных исходов будет n=36. Определит вероятность события: P=10/36=5/18.
В случае простого события и при бросании 2-х костей, требуется построить таблицу, затем в ней выделить нужные ячейки и их число поделить на 36, это и будет считаться вероятностью.
Парадокс Эльханана Мозеля
Задача
Вы бросаете игральную кость до тех пор, пока не выпадет 6. Каково среднее ожидаемое число бросков (включая тот, который дал 6) при условии, что во всех предыдущих бросках выпадали четные числа?
Подсказка 1
Большинство, в том числе и среди математиков, считает, что ответ равен 3. Они объясняют это примерно так: раз могут выпадать только четные числа, то задача эквивалентна бросанию кубика, у которого на двух гранях написано «2», на двух — «4», а еще на двух — «6». Но тогда вероятность выпадения грани «6» равна 1/3, следовательно, ожидаемое число бросков до выпадения первой шестерки равно 3.
Эти рассуждение и ответ — неправильны!
Подсказка 2
Давайте аккуратно опишем, как устроены бросания и в чем на самом деле состоит условие, что во всех предыдущих бросках выпадали четные числа. Мы рассматриваем (потенциально бесконечную) последовательность выпадения на кубике чисел 1, 2, 3, 4, 5, 6. Каждая последовательность заканчивается первым выпадением шестерки. Среди всех таких последовательностей выбираются только те, в которых до шестерки не было нечетных чисел 1, 3, 5. Спрашивается, какова «в среднем» длина таких последовательностей.
Решение
Разумеется, эту задачу можно решить с помощью «тяжелой артиллерии» типа формулы Байеса, но мы покажем очень элегантное и простое решение, придуманное Полом Каффом.
Пусть мы начинаем бросать кость и записываем результаты в строчку. Если выпадает нечетное число (1, 3, 5), то объявляем серию бросков неудачной и переходим на следующую строчку. Как только выпала шестерка — броски заканчиваются. Средняя длина последней строчки и будет ответом на задачу.
Отметим, что средняя длина последней строчки будет ровно такой же, как и средняя длина любой строчки. Это можно объяснить так. Рассмотрим бросание кубика, на котором написаны числа 2, 4, 6(1), 6(3), 6(5), 6. Пусть по-прежнему каждая из четырех шестерок заканчивает эксперимент (строчку), но если это «истинная» шестерка, то мы объявляем эксперимент удачным и подсчитываем число сделанных в нем бросков, а если это шестерка с нечетной цифрой в скобках, то объявляем эксперимент неудачным и забываем. Ясно, что средняя длина эксперимента не зависит от того, объявляли мы какие-то из экспериментов неудачными или нет. Поэтому достаточно сосчитать среднюю длину произвольной строчки.
В каждой написанной нами строчке все цифры, кроме последней — двойки и четверки. Любая из цифр 1, 3, 5, 6 заканчивает строчку, поэтому при каждом броске вероятность окончания строчки равна 4/6. Теперь если S — математическое ожидание длины строки (то, что мы имели в виду, говоря о «среднем ожидаемом числе бросков»), то S вычисляется из уравнения
откуда сразу находим S = 1,5. Смысл этого уравнения такой: с вероятностью 4/6 результатом броска будет цифра, которая закончит строчку, а с вероятностью 2/6 строчка продолжится. Но так как продолжение строчки состоит в таком же бросании кубика, то оно имеет среднюю длину, также равную S, то есть вся строчка, если она не закончилась сразу, имеет среднюю длину 1 + S.
Послесловие
Эту забавную головоломку предложил профессор MIT Эльханан Мозель (Elchanan Mossel). Строго говоря, она не является парадоксом, поскольку имеет четкое и совершенно строгое решение. Парадоксальность ей придает только то, что очень многие люди отказываются принимать это решение и настаивают на своей (ошибочной) версии с ответом 3.
Израильский математик Гиль Калай опубликовал задачу Мозеля в своем блоге под рубрикой TYI — test your intuition («проверьте свою интуицию»), предложив читателям блога выбрать один из вариантов ответа. Среди вариантов предлагались 1, 3/2, 2, 5/2, 3, 7/2 и 4. Поначалу перевес неправильного ответа «3» был просто подавляющим — количество выбравших его превышало 77%. Потом, после того, как в блоге Гиля появились несколько комментариев известных математиков о том, что задача не столь проста, как кажется на первый взгляд, результаты голосования чуть-чуть изменились. Однако и сейчас, на момент публикации Послесловия, на страничке голосования принят 1881 голос, из которых 975 (52%) предпочли вариант «3», а правильный ответ выбран всего 413 участниками (22%).
Разумеется, это не первая вероятностная задача, в которой интуитивно очевидный ответ оказывается неверным. Приведу еще несколько примеров таких задач. Начну с относительно малоизвестной.
Представьте, что в нашем распоряжении есть неограниченный запас белых и черных шариков и урна, в которой поначалу лежит всего два шарика — черный и белый. Мы начинаем повторять следующие действия:
1) вытаскиваем из урны случайный шарик;
2) возвращаем его обратно;
3) добавляем в урну еще один шарик того же цвета.
В какой-то момент количество шариков в урне станет равным 1000. Какова вероятность, что белых из них не менее 800?
Интуиция буквально кричит, что если в начале нам «повезет» и первый вытащенный шарик окажется белым, то дальше уже белый вытаскивается с вероятностью 2/3, а, следовательно, на очередном ходу в урне будет уже три белых шарика из четырех, и так далее. В общем, кажется, что попадание «на край», когда шариков одного цвета будет существенно больше, чем другого, является очень вероятным событием, — ну, а в половине таких случаев этот цвет окажется именно белым.
На самом же деле все расклады от 1:999 до 999:1 оказываются равновероятными (это называется равномерным распределением), поэтому вероятность наступления события «не менее 800 белых шариков» в точности равна отношению количества вариантов, в которых таких шариков не менее 800 (то есть 999 − 799 = 200), к общему количеству равновозможных вариантов (999). Ответ 200/999 настолько контринтуитивен, что в него просто невозможно поверить, пока не сосчитаешь аккуратно.
Еще один очень простой пример основан на бросании монетки (его часто называют нетранзитивной игрой Пеннея в честь Уолтера Пеннея, открывшего эту нетранзитивность в 1969 году).
Алиса и Боб бросают монетку до появления одной из двух комбинаций — «орел, орел, решка» или «решка, орел, орел». Первая из них (ООР) пусть будет выигрышем Алисы, а вторая (РОО) — выигрышем Боба. Кто будет выигрывать чаще, и во сколько раз?
Интуиция говорит, что если сами комбинации равновероятны, то Алиса и Боб будут выигрывать одинаково часто. Однако это вовсе не так (объяснение см., например, в статье «Лучшее пари для простаков», в которой приведены вероятности выигрыша для этой и других подобных игр). А в рассказе Сергея Мельникова «Прыжок через козла» описан случай, когда студенты-математики играют в эту игру со своим преподавателем физкультуры, чтобы получить у него зачет.
Пожалуй, еще более известным является «парадокс двух детей»:
У мистера Смита два ребенка, по крайней мере один из которых — мальчик. Чему равна вероятность того, что оба его ребенка — мальчики?
Правильным ответом на него обычно считается 1/3 (а не интуитивно напрашивающийся ответ 1/2), хотя на самом деле все немного сложнее, потому что у этой задачи нет однозначно понимаемой постановки. В частности, непонятно, как именно «случайно» выбирается один из детей Смита. Если мистер Смит выбирает одного из своих детей (старшего или младшего) с помощью подбрасывания монетки, а затем просто сообщает нам его пол при помощи словесной конструкции «по крайней мере один из моих детей — <мальчик/девочка>», то интуиция нас не обманывает: вероятность того, что пол другого ребенка будет таким же, строго равна 1/2.
Еще одной контринтуитивной вероятностной задаче была посвящена прошлогодняя задача «Игра в кости». Ну и, безусловно, в этом же ряду одно из почетных мест занимает задача Монти Холла, которой была посвящена одна из первых статей в задачном разделе на «Элементах».
Суммируем S*p(S): https://www.wolframalpha.com/input/?i=SUM(n%2F3%5En)
Неверный результат 0.75.
К сожалению, финт с S+1 мне остался непонятен.
Я так понимаю, формула суммирования тут неверна.
Суммарная вероятность всех исходов должна быть равна единице, потому что иначе мы как бы учитываем отброшенные броски. Более правильно считать как SUM( S * p(S) ) / SUM ( p(S) ), что как раз даёт 0.75 / 0.5 = 1.5
В целом вижу решение на пальцах.
Пусть из N бросков пусть мы получили 100 последовательностей из одной 6ки.
Последовательностей длиной два будет в 3 раза меньше, потому что нужно ещё выкинуть 2 или 4. Для длины 3 будет ещё в 3 раза меньше и т.д.
Ожидаемое среднее считается по формуле E(S) = ∑S * P(S)
P(S) = Кол-во бросков при длине S / всего бросков N
Первый игральный кубик обычный, а на гранях второго кубика нет нечетных чисел, а четные числа 2, 4 и 6 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 4 и 6 очков. Какова вероятность того, что бросали первый кубик?
Рассмотрим первый кубик. Распишем все варианты, когда могут выпасть очки 4 и 6:
| 1 бросок | 2 бросок |
| 4 | 6 |
| 6 | 4 |
Благоприятных исходов – 2, всевозможных – 6^2=36.
Значит, вероятность выпадения четырех и шести очков на первом кубике равна
Рассмотрим второй кубик. Выпишем все варианты, когда выпадают 4 и 6 очков, причем различать повторяющие очки будем знаком * (звездочка):
| 1 бросок | 2 бросок |
| 4 | 6 |
| 4 | 6* |
| 4* | 6 |
| 4* | 6* |
| 6 | 4 |
| 6 | 4* |
| 6* | 4 |
| 6* | 4* |
Значит, вероятность выпадения четырех и шести очков на втором кубике равна
Теперь пришло время найти вероятность того, что мы возьмем первый кубик из двух предложенных: