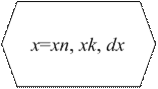Какой алгоритм является алгоритмом циклической структуры что такое параметр цикла
Какой алгоритм является алгоритмом циклической структуры что такое параметр цикла
Циклическим называется алгоритм, который содержит участок, выполняющийся многократно, каждый раз с новыми значениями переменных, изменяющихся по одним и тем же законам.
По способу организации циклы делятся на два основных вида:
начальное значение параметра (обозначим его 
конечное значение параметра (обозначим его 
Зная эти 3 величины, можно вычислить количество повторений цикла по формуле:
ПРИМЕР 4. Построить таблицу значений функции y = 2sin(x2-1) на заданном интервале изменения аргумента.
Математическая постановка задачи. Введем недостающие обозначения:
Выбор метода решения задачи. На каждом витке цикла будем выбирать точку (значение аргумента), вычислять в ней функцию и печатать оба значения в таблицу.
Знать принципы организации циклического алгоритма и уметь определять части цикла на схеме (даже «незнакомой» задачи) очень полезно. Это значительно облегчит Вам в дальнейшем процесс программирования алгоритма. Как правило, части цикла, касающиеся его организации (связанные с параметром цикла), описываются во всех языках программирования специальными операторами организации цикла. А действия, составляющие тело цикла, выделяются в отдельную группу операторов. Так что Вы сможете избежать ошибок программирования, если сейчас научитесь определять тело цикла на схеме алгоритма.
Внутри блока указываются параметр цикла, его начальное и конечное значения и шаг изменения в виде

Тело цикла обычно располагается ниже и более четко просматривается на схеме.
На рис.11 приведена типовая схема организации одиночного цикла с помощью блока «подготовка».
На рис.13 приведена схема решения задачи табулирования функции с помощью блока «подготовка». Сравните с предыдущей, «развернутой» схемой (рис.12).
Тело цикла на этой схеме составляют блоки 4, 5.
Количество повторений цикла (оно определяет количество строк в таблице значений функции) вычислим по формуле

Конечно, использование символа «подготовка» значительно сокращает размер циклической схемы и упрощает ее восприятие, но говорить о преимуществе того или иного варианта схемы не стоит, иногда при программировании более полезным оказывается именно «развернутый» вариант схемы. Все зависит от того, какими операторами описания цикла будет реализована конкретная схема.
Copyright © 2008-2021
Ющик Е.В. e-mail: veta@comp5.ru
Циклические структуры
Алгоритм циклической структуры – это алгоритм, в котором предусмотрено неоднократное выполнение одной и той же последовательности действий. На практике часто встречаются задачи, в которых одно или несколько действий бывает необходимо повторить несколько раз.
Многократное повторение последовательности действий называется циклом, а многократно повторяющиеся действия – телом цикла.
Изучение циклов демонстрирует учащимся главное преимущество компьютера перед человеком – выполнение большого числа действий за короткое время. Ведь даже весьма короткий циклический алгоритм, составить который не так уж долго, при исполнении может потребовать выполнения нескольких сотен действий, с которыми компьютер справится намного быстрее, чем человек.
Учащиеся должны уметь организовать цикл и верно определить тело цикла. Более того, при конструировании алгоритмов важно использовать такую конструкцию цикла, которая окажется оптимальной для решения поставленной задачи.
Существует три формы циклов: цикл с параметром, цикл с предусловием, цикл с постусловием. Каждая форма имеет стандартное описание на языке схем, а также соответствующий оператор алгоритмического языка.
а), б) – циклическая структура “Для каждого”
в) – циклическая структура “Пока”
г) – циклическая структура “До”
I – счетчик числа повторов, C – приращение счетчика, A – начальное значение счетчика, B – конечное значение счетчика, P – тело цикла.
1. Цикл “Для каждого” можно записать в следующем виде:
Для каждого I от A до B с шагом С:
I – счетчик числа повторов, C – приращение счетчика, A – начальное значение счетчика, B – конечное значение счетчика, P – тело цикла.
Турбо-Паскаль
2. Цикл “Пока” можно записать так:
Q – условие. ЭВМ будет выполнять P до тех пор, пока условие Q истинно.
Турбо-Паскаль
3. Цикл “До” записывается следующим образом:
Турбо-Паскаль
Тело цикла P выполняется до тех пор, пока условие Q ложно.
Одним из самых распространенных в практике вычислений алгоритмом циклической структуры является алгоритм вычислений некоторой функции y=f(x) для значений x, которые меняются от начального значения x0 до конечного xk с шагом h.
Исходными данными алгоритма являются значения: x0, xk, h. Необходимо вычисления по формуле y=f(x) повторять (xk-x0)/h+1 раз, т. е. при построении алгоритма организовать цикл. Параметром цикла выберем переменную x.
Схема алгоритма решения этой задачи на рис. 2. В схеме блок 3 присваивает начальное значение параметру цикла x, блок 6 осуществляет изменение на h параметра x при каждом выполнении цикла, блок 7 управляет циклом, для чего проверяется условие повторения цикла x 3.02.2005
АЛГОРИТМЫ ЦИКЛИЧЕСКОЙ СТРУКТУРЫ
Цикломназывают повторение одних и тех же действий (шагов).
Последовательность действий, которые повторяются в цикле, называют телом цикла. Существует несколько типов алгоритмов циклической структуры. На рис. 8 изображен цикл с предусловием, а на рис. 9 – цикл с постусловием, которые называют условными циклическими алгоритмами. Нетрудно заметить, что эти циклы взаимозаменяемы и обладают некоторыми отличиями. В цикле с предусловием условие проверяется до тела цикла, в цикле с постусловием – после тела цикла. В цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с предусловием тело цикла может не выполниться ни разу. В цикле с предусловием проверяется условие продолжения цикла, в цикле с постусловием – условие выхода из цикла.
При написании условных циклических алгоритмов следует помнить следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла. Кроме того, существует так называемый безусловный циклический алгоритм, который удобно использовать, если известно, сколько раз необходимо выполнить тело цикла. Выполнение безусловного циклического алгоритма начинается с присвоения переменной iстартового значения in. Затем следует проверка, не превосходит ли переменная iконечное значение iк. Если превосходит, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. В противном случае выполняется тело цикла, и переменная iменяет свое значение в соответствии с указанным шагом di. Далее, снова производится проверка значения переменной iи алгоритм повторяется. Понятно, что безусловный циклический алгоритм можно заменить любым условным.


Пример 1. Найти наибольший общий делитель (НОД) двух натуральных чисел (А, В).
Входные данные: А и В. Выходные данные: А – НОД.
Для решения поставленной задачи воспользуемся алгоритмом Евклида: будем уменьшать каждый раз большее из чисел на величину меньшего до тех пор, пока оба значения не станут равными, так, как показано в блок-схеме на рис. 11.
Пройдем алгоритм Евклида в соответствии с блок-схемой для поиска НОД чисел А=25 и В=15.
Исходные данные
| Первый шаг | Второй шаг | Третий шаг | НОД(А,В)=5 |
| А=25 | А=10 | А=10 | А=5 |
| В=15 | В=15 | В=5 | В=5 |
В блок–схеме для решения поставленной задачи используется цикл с предусловием, то есть тело цикла повторяется до тех пор, пока А не равно В.
Пример 2. Вводится последовательность чисел, 0 – конец последовательности. Определить, содержит ли последовательность хотя бы два равных соседних числа.
Например, в последовательности 7, 12, 25, 25, 6, 9, 9, 14, 0 – две пары равных соседних чисел: 25 и 9.
Входные данные: X0 – текущий член последовательности, X1 – следующий член последовательности.
Выходные данные:сообщение о наличии в последовательности двух равных соседних элементов. Усилим задачу подсчетом количества таких совпадающих пар.
Блок–схема решения задачи приведена на рис. 12. Применение здесь цикла с постусловием обосновано тем, что необходимо вначале сравнить два элемента последовательности, а затем принять решение об окончании цикла. Обратите внимание на то, что выражение «Х0 = Х1»в логическом блоке (ромб) имеет смысл сравнения, т.е. выясняется, совпадают ли эти значения, а в блоке присваивания (прямоугольник) эта же запись имеет смысл присваивания, т.е. в ячейку с именем Х0записывается числоХ1.
В приведенных примерах условие задачи таково, что неизвестно, сколько раз повторится тело цикла. Такие циклы называют циклами с неизвестным числом повторений (вообще говоря, неизвестно, закончится ли цикл вообще). Цикл, количество повторений которого известно заранее или его можно определить по исходным данным, называют циклом с известным числом повторений.
Рассмотрим несколько примеров с использованием таких циклов.
Пример 3. Составить таблицу значений функции y = e sin(x) cos(x)на отрезке [0;2]с шагом h= 0.1. Первый способ.
 |
 |
Входные данные:начальное значение аргумента A = 0, конечное значение аргумента B = 2, шаг изменения аргумента – 0.1.
Выходные данные:множество значений аргумента X и соответствующее им множество значений функции Y.
Пример 4. Составить таблицу значений функции y = e sin(x) cos(x)на отрезке [0;2]с шагом h= 0.1. Второй способ.
Входные данные:начальное значение аргумента A = 0, конечное значение аргумента B = 2, шаг изменения аргумента – 0.1.
Выходные данные:множество значений аргумента X и соответствующее им множество значений функции Y.

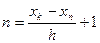
 | |
 | |
|
Выполнение алгоритма: здесь i –переменная типа пересчета,которая принимает значения 1, 2, …..( с шагом h=1) ; для каждого значения iдля текущего значенияХвычисляется соответствующее значение функции Y, до тех пор, пока переменная пересчета iне примет значение, равное n.
Пример 5. Вычислить факториал числаN (N!=1·2·3· …N).
Входные данные: N– целое число, факториал которого необходимо вычислить.
Выходные данные: Fact–значение факториала числа N, произведение чисел от 1 до N, целое число.
Промежуточные данные: i– целочисленная переменная, принимающая значения от 2 до N с шагом 1, параметр цикла. Блок-схема приведена на рис.15.
Итак, вводится число N. Переменной Fact,предназначенной для хранения значения произведения последовательности чисел, присваивается начальное значение, равное единице. Затем организуется цикл, параметром которого выступает переменная i. Если значение параметра цикла меньше или равно N, то выполняется оператор тела цикла, в котором из участка памяти с именем Factсчитывается предыдущее значение произведения, умножается на текущее значение параметра цикла, а результат снова помещается в участок памяти с именем Fact. Когда параметр i становится больше N,цикл заканчивается, и на печать выводится значение переменой Fact,которая была вычислена в теле цикла.
Пример 6.Вычислить a n (n>0).
Входные данные: a– вещественное число, которое необходимо возвести в целую положительную степень n.
Выходные данные: p (вещественное число) –результат возведения вещественного числа a в целую положительную степень n.
Промежуточные данные: i– целочисленная переменная, принимающая значения от 1 до nс шагом 1, параметр цикла. Блок-схема приведена на рис.16.
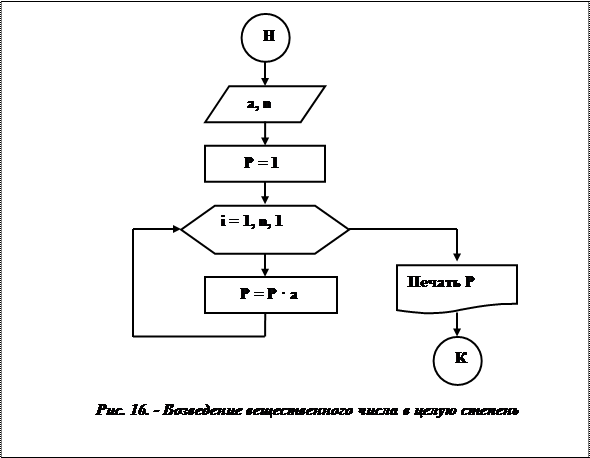 |
Итак, известно, что для того, чтобы получить целую степень n числа a, нужно умножить его само на себя n раз. Результат этого умножения будет храниться в участке памяти с именем Р. При выполнении очередного цикла из этого участка предыдущее значение будет считываться, умножаться на основание степени a и снова записываться в участок памяти Р. Цикл выполняется nраз.
В следующей таблице отображен протокол выполнения алгоритма при возведении числа 2
в пятую степень: a=2, n=5. Подобные таблицы, заполненные вручную, используются для тестирования – проверки всех этапов работы программы.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Алгоритмы циклической структуры
Алгоритмы циклической структуры являются наиболее распространённым видом алгоритмов. В алгоритмахциклической структуры в зависимости от выполнения или невыполнения какого-либо условия выполняется повторяющаяся последовательность действий, называющаяся телом цикла.
Классическим примером использования структуры «Цикл» является задача табулирования функции. Задача табулирования (получение таблицы) некоторой функции y = f(x) сводится к вычислению значений этой функции при параметре цикла х, изменяющемся с постоянным шагом Dx в заданном диапазоне от начального значения аргумента xn до конечного значения xk. На экран монитора выводится ](xk – xn)/Dx[+ 1 пар значений аргумента x с помощью оператора вывода, расположенного внутри тела цикла. Скобки ][ означают, что берётся целая часть от деления.
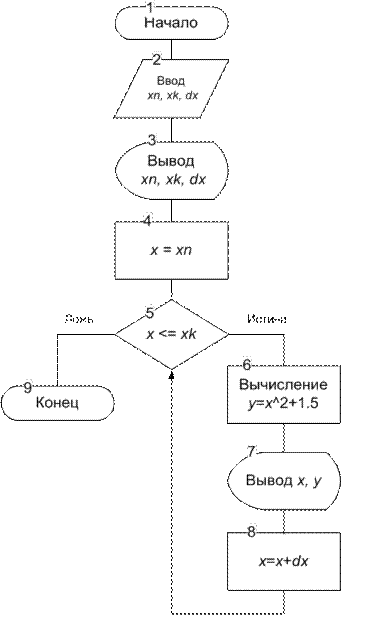
Пример. Вычислить значение функции y(x) = x 2 + 1,5 при изменении аргумента x в диапазоне xn ≤ x ≤ xk с шагом Dx. Вывести таблицу значений x и y.
Визуальное представление алгоритма решения задачи в виде цикла типа «ПОКА» с предусловием дано на рисунке 9.13
Рис. 9.13. Визуальное представление алгоритма табулирования функции в виде цикла типа «ПОКА» − цикл с предусловием
Это цикл с заданным числом повторений ](xk – xn)/Dx[ + 1. Перед первым выполнением цикла необходимо задать начальное значение аргумента x, равное xn, а затем ](xk – xn)/Dx[ + 1 раз выполнить вычисление и вывод значений функции y. При каждом новом выполнении цикла необходимо изменять аргумент на величину шага, равного Dx. Чтобы процесс не был бесконечным, необходимо задать условие повторения или окончания цикла.
В схеме циклического алгоритма присутствуют обязательные блоки в этих структурах: установка начального значения параметра (блок 4), проверка условия достижения конечного значения параметра (блок 5), изменение параметра (блок 8).
Телом данного циклического процесса являются блоки 5, 6, 7 и 8. Параметром данного цикла является переменная x.
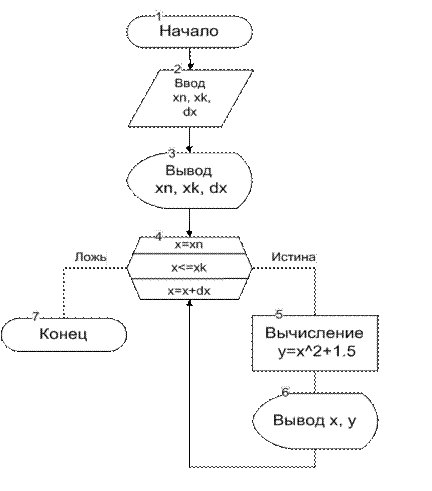
Представим данную схему циклического алгоритма с помощью цикла типа «ДЛЯ», или цикла с параметром, который является модификацией цикла «ПОКА» для ситуации, когда заранее известно количество повторений некоторых действий. В этом случае все три необходимых блока – блок 4, блок 5 и блок 8 – собираются в один блок – блок 4 (рис. 9.14), в котором указываются начальное и конечное значения параметра и шаг изменения.
Рис. 9.14. Визуальное представление алгоритма табулирования функции в виде цикла типа«ДЛЯ», или цикла с параметром
На рисунке 9.14 блок 4 для большей наглядности изображён в «развёрнутом» виде. Общепринятым является компактное изображение такого блока в виде символа «Подготовка» (рис. 9.15). Именно такое представление мы будем использовать в дальнейшем. Если dx отсутствует, то по умолчанию dx = 1.
Рис. 9.15. Представление цикла с параметром символом «Подготовка»
Приведем несколько тестовых заданий с решениями.
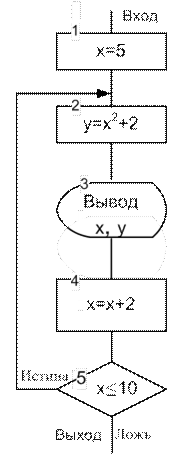
Укажите, какие результаты будут выведены на экран монитора при выполнении следующего фрагмента алгоритма (рис. 9.16):
Рис. 9.16. Рисунок к заданию 9.9
| Блок 1. Переменной x присваивается значение 5, x=5. | |
| цикл | Блок 2. Вычисляется значение переменной y=x 2 +2=5 2 +2=27. Блок 3. На экран монитора выводятся значения переменных x = 5 и y = 27. Блок 4. Переменной x присваивается новое значение: x = x + 2 = 5 + 2 = 7. Блок 5. Выполняется проверка условия x ≤ 10; подставляя новое значение x = 7, получим 7 ≤ 10; условие выполняется, следовательно, после блока 5 выполняется блок 2. |
| цикл | Блок 2. Вычисляется значение переменной с новым значением x = 7, y = x 2 + 2 = 7 2 + 2 = 51. Блок 3. На экран выводятся значения переменных x = 7 и y = 51. Блок 4. Переменной x присваивается новое значение: x = x + 2 = 7 + 2 = 9. Блок 5. Выполняется проверка условия x ≤ 10; подставляя новое значение x = 9, получим 9 ≤ 10; условие выполняется, следовательно, после блока 5 выполняется блок 2. |
| цикл | Блок 2. Вычисляется значение переменной с новым значением x = 9, y = x 2 +2=9 2 +2=83. Блок 3. На экран выводятся значения переменных x = 9 и y = 83. Блок 4. Переменной x присваивается новое значение: x = x + 2 = 9 + 2 = 11. Блок 5. Выполняется проверка условия x ≤ 10; подставляя новое значение x = 11, получим 11 ≤ 10; условие не выполняется, следовательно, после блока 5 выполняется выход из данного фрагмента алгоритма. |
Таким образом, данный фрагмент алгоритма описывает задачу табулирования (получение таблицы) функции y = f(х) = x 2 +2. Вычисляются значения этой функции при параметре цикла х, изменяющемся с постоянным шагом Dx = 2 в заданном диапазоне от начального значения аргумента xn=5 до конечного значения xk = 10. На экран выводится ](xk – xn)/Dx[+ 1=3 пар значений аргумента x с помощью блока вывода, расположенного внутри тела цикла. Результатом выполнения данного циклического алгоритма является следующий список значений (аргумента x и функции y):
Так как в алгоритме сначала выполняется действие, а потом проверка окончания циклического процесса, следовательно, в данном алгоритме реализована разновидность базовой управляющей структуры «цикл с постусловием» типа «ДО».
Блоки 2÷5 являются телом цикла. Переменная x − параметр цикла. Количество повторений цикла − 3.
Этот же алгоритм может быть реализован в виде «цикла с предусловием» (рис. 9.13) и «цикла с параметром» (рис. 9.14).
Укажите, какие результаты будут выведены на экран монитора при выполнении следующего фрагмента алгоритма (рис. 9.17):
Рис. 9.17. Визуальное представление алгоритма накопления суммы
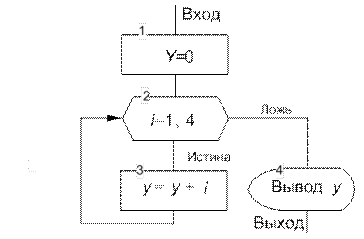
| Блок 1. Переменной Y присваивается значение 0, Y = 0. | |
| цикл | Блок 2 представляет собой символ «подготовка». Его назначение − заголовок цикла (рис. 9.14, блок 4 и рис.9.15), в котором указывается начальное (iн=1), конечное значение параметра цикла i (iк=4) и шаг его изменения (iш=1). Следовательно, на данном шаге параметр цикла принимает начальное значение i=1. Блок 3. Переменная y принимает новое значение y=y+i=0+1=1. После блока 3 выполняется блок 2. |
| цикл | Блок 2. Согласно назначению блока 2, который представляет собой заголовок цикла (рис. 9.15), на следующем этапе переменная цикла i принимает новое значение, увеличенное на шаг i =i+1=1+1=2, после этого проверяется условие окончания циклического процесса путем сравнения текущего значения параметра цикла i и его конечного значения − i≤ 4? На данном этапе условие 2 ≤ 4 выполняется, следовательно, блок 3 повторяется для нового значения i. Блок 3. Переменная y принимает новое значение y = y+i = 1+2=3. После блока 3 выполняется блок 2. |
| цикл | Блок 2. Переменная цикла i принимает новое значение, увеличенное на шаг i = i+1=2+1=3, после этого проверяется условие окончания циклического процесса путем сравнения текущего значения параметра цикла i и его конечного значения − i≤ 4? На данном этапе условие 3 ≤ 4 выполняется, следовательно, блок 3 повторяется для нового значения i. Блок 3. Переменная y принимает новое значение y=y+i=3+3=6. После блока 3 снова выполняется блок 2. |
| цикл | Блок 2. Переменная цикла i принимает новое значение, увеличенное на шаг i = i + 1 = 3 + 1 = 4, после этого проверяется условие окончания циклического процесса путём сравнения текущего значения параметра цикла i и его конечного значения − i ≤ 4? На данном этапе условие 4 ≤ 4 выполняется, следовательно, блок 3 повторяется для нового значения i. Блок 3. Переменная y принимает новое значение y=y+i=6+4=10. После блока 3 снова выполняется блок 2. |
| Блок 2. Переменная цикла i принимает новое значение, увеличенное на шаг i = i+1=4+1=5, после этого снова проверяется условие окончания циклического процесса путём сравнения текущего значения параметра цикла i и его конечного значения − i ≤ 4? На данном этапе условие 5 ≤ 4 не выполняется, следовательно, происходит окончание циклического процесса. После блока 2 в этом случае выполняется блок 4. | |
| Блок 4. На экран монитора выводится y = 10. |
Количество повторений цикла − 4.
Нетрудно увидеть, что в данном фрагменте описан алгоритм накопления суммы, в данном алгоритме y = 0+1+2+3+4.
Присвоение начального значения переменной y, в которой накапливается сумма, выполняется перед циклом. Вывод результата, поскольку он единственный, осуществляют после окончания работы цикла.
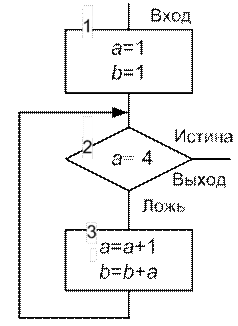
Укажите, какие значения примут переменные a и b после выполнениия следующего фрагмента алгоритма (рис 9.18):
Рис. 9.18. Фрагмент схемы алгоритма к заданию 9.11
Выполним алгоритм последовательно.
| Блок 1. а=1, b=1. | |
| цикл | Блок 2. a = 4? 1 = 4? Нет, следовательно, выполняем блок 3. Блок 3. a = a+1=1+1=2, b=b+a=1+2=3. После блока 3 согласно схеме алгоритма всегда выполняется блок 2. |
| цикл | Блок 2. a = 4?, 2=4? Нет, следовательно, выполняем блок 3. Блок 3. a = a+1=2+1=3, b=b+a=3+3=6. После блока 3 всегда выполняется блок 2. |
| цикл | Блок 2. a = 4? 3 = 4? Нет, следовательно, выполняем блок 3. Блок 3. a = a+1=3+1=4, b=b+a=6+4=10. |
| Блок 2 a=4? 4=4? Да, следовательно, происходит выход из цикла. |
Переменная b после окончания циклического процесса равна 10, а переменная а приняла значение 4. Данный алгоритм представляет собой «цикл с предусловием». Количество повторений тела цикла равно 3.
Дата добавления: 2015-09-14 ; просмотров: 1098 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ