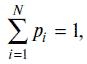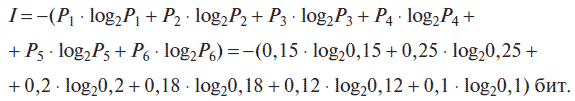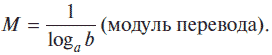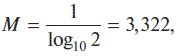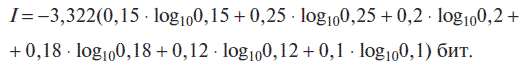Какой шаблон предполагает что 1 единица информации равняется 1 2 строки

1.2. Определение количества информации. Единицы измерения количества информации

1.2. Определение количества информации. Единицы измерения количества информации

Как уже отмечалось, понятие информации можно рассматривать при различных ограничениях, накладываемых на ее свойства, т. е. при различных уровнях рассмотрения. В основном выделяют три уровня – синтаксический, семантический и прагматический. Соответственно на каждом из них для определения количества информации применяют различные оценки.

На синтаксическом уровне для оценки количества информации используют вероятностные методы, которые принимают во внимание только вероятностные свойства информации и не учитывают другие (смысловое содержание, полезность, актуальность и т. д.). Разработанные в середине XX в. математические и, в частности, вероятностные методы позволили сформировать подход к оценке количества информации как к мере уменьшения неопределенности знаний. Такой подход, называемый также вероятностным, постулирует принцип: если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно утверждать, что такое сообщение содержит информацию. При этом сообщения содержат информацию о каких-либо событиях, которые могут реализоваться с различными вероятностями. Формулу для определения количества информации для событий с различными вероятностями и получаемых от дискретного источника информации предложил американский ученый К. Шеннон в 1948 г. Согласно этой формуле количество информации может быть определено следующим образом:

Определяемое с помощью формулы (1.1) количество информации принимает только положительное значение. Поскольку вероятность отдельных событий меньше единицы, то соответственно выражение log^,– является отрицательной величиной и для получения положительного значения количества информации в формуле (1.1) перед знаком суммы стоит знак минус.

Если вероятность появления отдельных событий одинаковая и они образуют полную группу событий, т. е.

то формула (1.1) преобразуется в формулу Р. Хартли:

В формулах (1.1) и (1.2) отношение между количеством информации и соответственно вероятностью, или количеством, отдельных событий выражается с помощью логарифма. Применение логарифмов в формулах (1.1) и (1.2) можно объяснить следующим образом. Для простоты рассуждений воспользуемся соотношением (1.2). Будем последовательно присваивать аргументу N значения, выбираемые, например, из ряда чисел: 1, 2, 4, 8, 16, 32, 64 и т. д. Чтобы определить, какое событие из N равновероятных событий произошло, для каждого числа ряда необходимо последовательно производить операции выбора из двух возможных событий. Так, при N = 1 количество операций будет равно 0 (вероятность события равна 1), при N = 2, количество операций будет равно 1, при N = 4 количество операций будет равно 2, при N = 8, количество операций будет равно 3 и т. д. Таким образом получим следующий ряд чисел: 0, 1, 2, 3, 4, 5, 6 и т. д., который можно считать соответствующим значениям функции I в соотношении (1.2). Последовательность значений чисел, которые принимает аргумент N, представляет собой ряд, известный в математике как ряд чисел, образующих геометрическую прогрессию, а последовательность значений чисел, которые принимает функция I, будет являться рядом, образующим арифметическую прогрессию. Таким образом, логарифм в формулах (1.1) и (1.2) устанавливает соотношение между рядами, представляющими геометрическую и арифметическую прогрессии, что достаточно хорошо известно в математике.

Для количественного определения (оценки) любой физической величины необходимо определить единицу измерения, которая в теории измерений носит название меры. Как уже отмечалось, информацию перед обработкой, передачей и хранением необходимо подвергнуть кодированию. Кодирование производится с помощью специальных алфавитов (знаковых систем). В информатике, изучающей процессы получения, обработки, передачи и хранения информации с помощью вычислительных (компьютерных) систем, в основном используется двоичное кодирование, при котором используется знаковая система, состоящая из двух символов 0 и 1. По этой причине в формулах (1.1) и (1.2) в качестве основания логарифма используется цифра 2.

Исходя из вероятностного подхода к определению количества информации эти два символа двоичной знаковой системы можно рассматривать как два различных возможных события, поэтому за единицу количества информации принято такое количество информации, которое содержит сообщение, уменьшающее неопределенность знания в два раза (до получения событий их вероятность равна 0,5, после получения – 1, неопределенность уменьшается соответственно: 1/0,5 = 2, т. е. в 2 раза). Такая единица измерения информации называется битом (от англ. слова binary digit – двоичная цифра). Таким образом, в качестве меры для оценки количества информации на синтаксическом уровне, при условии двоичного кодирования, принят один бит.

Следующей по величине единицей измерения количества информации является байт, представляющий собой последовательность, составленную из восьми бит, т. е.

1 байт = 2 3 бит = 8 бит.

Кратные байту единицы измерения количества информации вводятся следующим образом:

1 Килобайт (Кбайт) = 2 10 байт = 1024 байт,

1 Мегабайт (Мбайт) = 2 10 Кбайт = 1024 Кбайт,

1 Гигабайт (Гбайт) = 2 10 Мбайт = 1024 Мбайт,

1 Терабайт (Тбайт) = 2 10 Гбайт = 1024 Гбайт,

1 Петабайт (Пбайт) = 2 10 Тбайт = 1024 Тбайт,

1 Экзабайт (Эбайт) = 2 10 Пбайт = 1024 Пбайт.

Вероятностный подход используется и при определении количества информации, представленной с помощью знаковых систем. Если рассматривать символы алфавита как множество возможных сообщений N, то количество информации, которое несет один знак алфавита, можно определить по формуле (1.1). При равновероятном появлении каждого знака алфавита в тексте сообщения для определения количества информации можно воспользоваться формулой (1.2).

Количество информации, которое несет один знак алфавита, тем больше, чем больше знаков входит в этот алфавит. Количество знаков, входящих в алфавит, называется мощностью алфавита. Количество информации (информационный объем), содержащееся в сообщении, закодированном с помощью знаковой системы и содержащем определенное количество знаков (символов), определяется с помощью формулы:

где V – информационный объем сообщения; / = log 2N, информационный объем одного символа (знака); К – количество символов (знаков) в сообщении; N – мощность алфавита (количество знаков в алфавите).

Поясним вышесказанное в п. 1.2 на примерах.

Определим, какое количество информации можно получить после реализации одного из шести событий. Вероятность первого события составляет 0,15; второго – 0,25; третьего – 0,2; четвертого – 0,12; пятого – 0,12; шестого – 0,1, т. е. Р 1 = 0,15; Р 2 = 0,25; Р 3 = 0,2; Р 4 = 0,18; Р 5 = 0,12; Р 6 = 0,1.

Для определения количества информации применим формулу (1.1)

Для вычисления этого выражения, содержащего логарифмы, воспользуемся сначала компьютерным калькулятором, а затем табличным процессором Microsoft (MS) Excel, входящим в интегрированный пакет программ MS Office ХР.

Для вычисления с помощью компьютерного калькулятора выполним следующие действия.

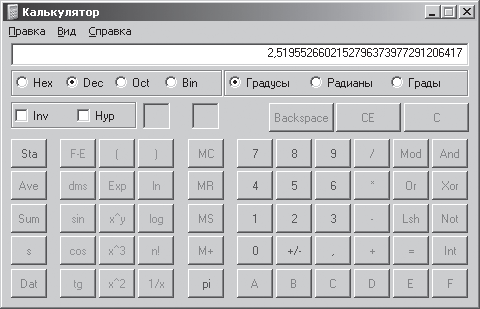
С помощью команды: [Кнопка Пуск – Программы – Стандартные – Калькулятор] запустим программу Калькулятор. После запуска программы выполним команду: [Вид – Инженерный] (рис. 1.3).

Рис. 1.3. Инженерный калькулятор

Кнопка log калькулятора производит вычисление десятичного (по основанию 10) логарифма отображаемого числа. Поскольку в нашем случае необходимо производить вычисления логарифмов по основанию 2, а данный калькулятор не позволяет этого делать, то необходимо воспользоваться известной формулой:

В нашем случае соотношение примет вид: log 2N = M log 10N,

т. е log 2N = 3,322 · log 10N, и выражение для вычисления количества информации примет вид:

При вычислении на калькуляторе используем кнопки: +/- (изменение знака отображаемого числа),() (открывающие и закрывающие скобки), log (логарифм числа по основанию 10) и т. д. Результат вычисления показан на рис. 1.3. Таким образом, количество информации I = 2,52 бит.

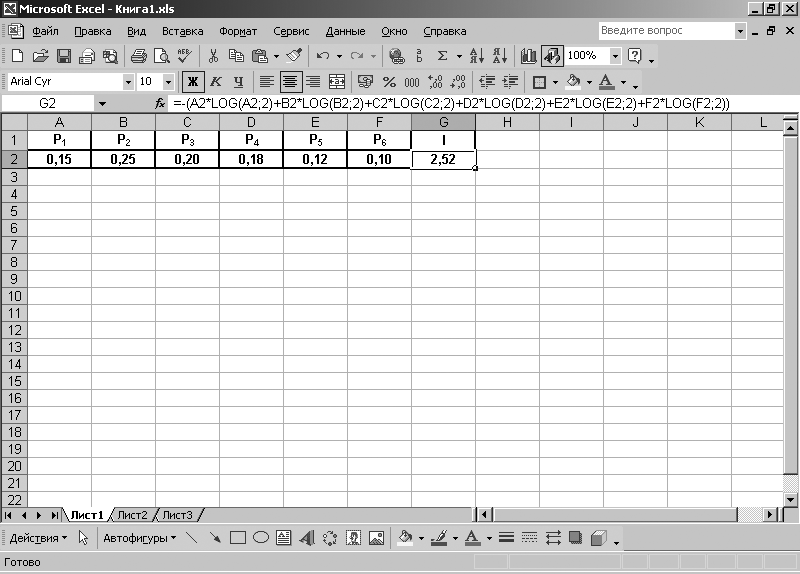
После записи значений в ячейки необходимо установить в них формат числа. Для этого необходимо выполнить следующую команду: [Формат – Ячейки – Число – Числовой (устанавливаем число десятичных знаков, равное двум) ]. Устанавливаем в ячейке G2 тот же числовой формат. В ячейку G2 записываем выражение = – (A2*LOG(A2;2) + B2*LOG(B2;2) + C2*LOG(C2;2) + D2*LOG(D2;2) + E2*LOG(E2;2) + F2*LOG(F2;2) ). После нажатия на клавиатуре компьютера клавиши , в ячейке G2 получим искомый результат – I = 2,52 бит (рис. 1.4).

Рис. 1.4. Результат вычисления количества информации

Пример 1.2

Определим, какое количество байт и бит информации содержится в сообщении, если его объем составляет 0,25 Кбайта.

С помощью калькулятора определим количество байт и бит информации, которое содержится в данном сообщении:

I = 0,25 Кбайт · 1024 байт/1 Кбайт = 256 байт;

I = 256 байт · 8 бит/1 байт = 2048 бит.

Пример 1.3

Определим мощность алфавита, с помощью которого передано сообщение, содержащее 4096 символов, если информационный объем сообщения составляет 2 Кбайта.

С помощью калькулятора переведем информационный объем сообщения из килобайт в биты:

V = 2 Кбайт 1024 байт/1 Кбайт = 2048 байт 8 бит/1 байт = 16384 бит.

Определим количество бит, приходящееся на один символ (информационный объем одного символа) в алфавите:

I = 16 384 бит/4096 = 4 бит.

Используя формулу (1.3), определим мощность алфавита (количество символов в алфавите) :

Как уже отмечалось, если принять во внимание только свойство информации, связанное с ее смысловым содержанием, то при определении понятия информации можно ограничиться смысловым, или семантическим, уровнем рассмотрения этого понятия.

На семантическом уровне информация рассматривается по ее содержанию, отражающему состояние отдельного объекта или системы в целом. При этом не учитывается ее полезность для получателя информации. На данном уровне изучаются отношения между знаками, их предметными и смысловыми значениями (см. рис. 1.1), что позволяет осуществить выбор смысловых единиц измерения информации. Поскольку смысловое содержание информации передается с помощью сообщения, т. е. в виде совокупности знаков (символов), передаваемых с помощью сигналов от источника информации к приемнику, то широкое распространение для измерения смыслового содержания информации получил подход, основанный на использовании тезаурусной меры. При этом под тезаурусом понимается совокупность априорной информации (сведений), которой располагает приемник информации.

Данный подход предполагает, что для понимания (осмысливания) и использования полученной информации приемник (получатель) должен обладать априорной информацией (тезаурусом), т. е. определенным запасом знаков, наполненных смыслом, слов, понятий, названий явлений и объектов, между которыми установлены связи на смысловом уровне. Таким образом, если принять знания о данном объекте или явлении за тезаурус, то количество информации, содержащееся в новом сообщении о данном предмете, можно оценить по изменению индивидуального тезауруса под воздействием данного сообщения. В зависимости от соотношений между смысловым содержанием сообщения и тезаурусом пользователя изменяется количество семантической информации, при этом характер такой зависимости не поддается строгому математическому описанию и сводится к рассмотрению трех основных условий, при которых тезаурус пользователя:

• стремится к нулю, т. е. пользователь не воспринимает поступившее сообщение;

• стремится к бесконечности, т. е. пользователь досконально знает все об объекте или явлении и поступившее сообщение его не интересует;

• согласован со смысловым содержанием сообщения, т. е. поступившее сообщение понятно пользователю и несет новые сведения.

Два первых предельных случая соответствуют состоянию, при котором количество семантической информации, получаемое пользователем, минимально. Третий случай связан с получением максимального количества семантической информации. Таким образом, количество семантической информации, получаемой пользователем, является величиной относительной, поскольку одно и то же сообщение может иметь смысловое содержание для компетентного и быть бессмысленным для некомпетентного пользователя.

Поэтому возникает сложность получения объективной оценки количества информации на семантическом уровне ее рассмотрения и для получения такой оценки используют различные единицы измерения количества информации: абсолютные или относительные. В качестве абсолютных единиц измерения могут использоваться символы, реквизиты, записи и т. д., а в качестве относительной – коэффициент содержательности, который определяется как отношение семантической информации к ее объему. Например, для определения на семантическом уровне количества информации, полученной студентами на занятиях, в качестве единицы измерения может быть принят исходный балл (символ), характеризующий степень усвояемости ими нового учебного материала, на основе которого можно косвенно определить количество информации, полученное каждым студентом. Это количество информации будет выражено через соответствующий оценочный балл в принятом диапазоне оценок.

При семантическом подходе к оценке количества информации и выборе единицы измерения существенным является вид получаемой информации (сообщения). Так, данный подход к оценке количества экономической информации позволяет выявить составную единицу экономической информации, состоящую из совокупности других единиц информации, связанных между собой по смыслу. Элементарной составляющей единицей экономической информации является реквизит, т. е. информационная совокупность, которая не поддается дальнейшему делению на единицы информации на смысловом уровне. Деление реквизитов на символы приводит к потере их смыслового содержания. Каждый реквизит характеризуется именем, значением и типом. При этом под именем реквизита понимается его условное обозначение, под значением – величина, характеризующая свойства объекта или явления в определенных обстоятельствах, под типом – множество значений реквизита, объединенных определенными признаками и совокупностью допустимых преобразований.

Реквизиты принято делить на реквизиты-основания и реквизиты-признаки [2].

Реквизиты-основания характеризуют количественную сторону экономического объекта, процесса или явления, которые могут быть получены в результате совершения отдельных операций – вычислений, измерений, подсчета натуральных единиц и т. д. В экономических документах к ним можно отнести, например, цену товара, его количество, сумму и т. п. Реквизиты-основания чаще всего выражаются в цифрах, над которыми могут выполняться математические операции.

Реквизиты-признаки отражают качественные свойства экономического объекта, процесса или явления. С помощью реквизитов-признаков сообщения приобретают индивидуальный характер. В экономических документах к ним можно отнести, например, номер документа, имя отправителя, дату составления документа, вид операции и т. п. Реквизиты-признаки позволяют осуществлять логическую обработку единиц количества информации на семантическом уровне: поиск, выборку, группировку, сортировку и т. д.

Отдельный реквизит-основание вместе с относящимися к нему реквизитами-признаками образует следующую в иерархическом отношении составную единицу экономической информации – показатель. Показатель имеет наименование, в состав которого входят термины, обозначающие измеряемый объект: себестоимость, затраты, мощность, прибыль и т. д. Кроме того, показатель содержит формальную характеристику и дополнительные признаки. К формальной характеристике относится способ его получения (объем, сумма, прирост, процент, среднее значение и т. д.), а к дополнительным – пространственно-временные (где находится измеряемый объект, время, к которому относится данный показатель) и метрологические (единицы измерения).

Таким образом, с помощью совокупности реквизитов и соответствующих им показателей можно оценить количество экономической информации, получаемой от исследуемого объекта (источника информации).

Кроме подхода, основанного на использовании тезаурусной меры, при определении количества информации на семантическом уровне находят применение и другие подходы [1]. Например, один из подходов, связанных с семантической оценкой количества информации, заключается в том, что в качестве основного критерия семантической ценности информации, содержащейся в сообщении, принимается количество ссылок на него в других сообщениях. Количество получаемой информации определяется на основе статистической обработки ссылок в различных выборках.

Подводя итог сказанному, можно утверждать, что существовала и существует проблема формирования единого системного подхода к определению информации на семантическом уровне. Это подтверждается и тем, что в свое время для создания строгой научной теории информации К. Шеннон вынужден был отбросить важное свойство информации, связанное со смысловым ее содержанием.

Кроме перечисленных уровней рассмотрения понятия информации достаточно широко используется прагматический уровень. На данном уровне информация рассматривается с точки зрения ее полезности (ценности) для достижения потребителем информации (человеком) поставленной практической цели. Данный подход при определении полезности информации основан на расчете приращения вероятности достижения цели до и после получения получения информации [1]. Количество информации, определяющее ее ценность (полезность), находится по формуле:

где Р 0, P 1 – вероятность достижения цели соответственно до и после получения информации.

В качестве единицы измерения (меры) количества информации, определяющей ее ценность, может быть принят 1 бит (при основании логарифма, равном 2), т. е. это такое количество полученной информации, при котором отношение вероятностей достижения цели равно 2.

Рассмотрим три случая, когда количество информации, определяющее ее ценность, равно нулю и когда она принимает положительное и отрицательное значение.

Количество информации равно нулю при Р 0 = Р 1, т.е. полученная информация не увеличивает и не уменьшает вероятность достижения цели.

Значение информации является положительной величиной при P 1 > P 0, т. е. полученная информация уменьшает исходную неопределенность и увеличивает вероятность достижения цели.

Значение информации является отрицательной величиной при P 1 0, т. е. полученная информация увеличивает исходную неопределенность и уменьшает вероятность достижения цели. Такую информацию называют дезинформацией.

Дальнейшее развитие данного подхода базируется на статистической теории информации и теории решений. При этом кроме вероятностныхарактеристик достижения цели после получения информации вводятся функции потерь и оценка полезности информации производится в результате минимизации функции потерь. Максимальной ценностью обладает то количество информации, которое уменьшает потери до нуля при достижении поставленной цели [1].

Данный текст является ознакомительным фрагментом.

Источник

Измерение информации, алфавитный подход. Методическая разработка по теме, предназначенная для уроков в 10–11-х классах с углубленным изучением информатики с целью подготовки к ГИА

Ключевые слова: ГИА по информатике

Презентация к уроку

На уроках информатики мы никогда ничего не зубрим! Ученики должны понимать все, о чем говорится на уроках, и запоминать новое путем повторений пройденного материала, сравнений и ассоциаций с уже знакомыми темами и понятной информацией.

В данной методике рассматривается алфавитный подходк измерению информации.

При изучении данной темы обращаем особое внимание на таблицы степеней двойки и соответствия единиц измерения количества информации, а так же их взаимосвязь, что послужит изложенному выше принципу решения задач.

При этом знание таблиц является необходимым условием для максимально быстрого и точного решения, без потери времени и математических ошибок.

Байт содержит 8 бит (23 бит). При этом байт является неделимой единицей и всегда отображается целым числом.

Во второй таблице даны укрупненные единицы информации и их соответствие.

В России правила образования укрупненных единиц в информатике подтверждены постановлением № 879 Правительства РФ от 31 октября 2009г. Это постановление гласит:

«Наименование и обозначение единицы количества информации «байт» применяются с двоичными приставками «Кило», «Мега», «Гига», которые соответствуют множителям 210, 220 и 230 (1 Килобайт = 1024 байт, 1 Мегабайт = 1024 Килобайт,

1 Гигабайт = 1024 Мегабайт). Эти приставки пишутся с большой буквы».

Таким образом, каждая следующая единица измерения количества информации в 1024 = 210 раза больше предыдущей, на основании чего и строится таблица их соответствия:

В бит=

В бит / байт

Примечание

1 Кбит (один Килобит)

1 Гбит (один Гигабит)

1 Кбайт (один Килобайт)

210 байт = 1024 байт

1 Мбайт (один Мегабайт)

220 байт = 1 048 576 байт

1 Гбайт (один Гигабайт)

230 байт = 109 байт

Таблицы не нужно учить наизусть! Рекомендуется пользоваться ими при решении задач, но при этом заглядывать в них все реже и реже, пытаясь сначала вспомнить значения, приведенные в них. Тогда эти таблицы сами «улягутся» в Вашей голове, и очень поможет Вам на экзамене в этой и в других темах!

Отцом-основателем теории информации, нашедшей применение в современных высокотехнологических системах связи, является американский инженер, криптоаналитик и математик Клод Шеннон. Именно он в 1948 году предложил использовать слово «бит» для обозначения наименьшей единицы измерения информации (в статье «Математическая теория связи»). Кроме того, понятие энтропии было важной особенностью теории Шеннона. Он продемонстрировал, что введённая им энтропия эквивалентна мере неопределённости информации в передаваемом сообщении, что и лежит в основе содержательного подхода к измерению информации, который в данной разработке нами не рассматривается. Статьи Шеннона «Математическая теория связи» и «Теория связи в секретных системах» считаются основополагающими для теории информации и криптографии.

В начале 60-х гг. русский советский математик, один из крупнейших математиков XX века Андрей Николаевич Колмогоров начал искать пути построения теории информации и теории вероятностей на принципиально новой, алгоритмической основе. В свое первой статье по алгоритмической теории информации «Три подхода к определению понятия «количество информации», вышедшей в первом выпуске первого тома журнала «Проблемы передачи информации», в 1965г, А.Н.Колмогоров указал способ измерения сложности конечного объекта (слова), для чего он ввел понятие, называемое сейчас «колмогоровской сложностью». Свое новое понятие он применил для построения алгоритмического варианта теории информации, позволяющего измерять информацию в конечной строке знаков.

Согласно Колмогорову, количество информации, содержащейся в тексте, определяется минимально возможной длиной двоичного кода, необходимого для представления этого текста.

Формула была предложена Ральфом Хартли в 1928 году как один из научных подходов к оценке сообщений.

Для случая определения количества информации k в одном символе (бит на символ) алфавита мощности М, формула Хартли принимает вид:

Соответственно, мощность алфавита равна:

M= 2 k

Из формулы Хартли следует, что алфавит, содержащий только 1 символ, не может быть использован для передачи информации, так как

Пусть, имеется алфавит, из Mбукв которого составляется сообщение.

Количество возможных вариантов Q всех возможных «слов» (символьных цепочек без учета смысла) длиной N равно

Q = М k

Для простоты понимания и решения задач, за М мы будем принимать значения терминов, наиболее часто применяемых в условиях задач – виды, типы, состояния символов. Это упростит понимание и решение задач в алфавитном подходе.

Отметим, что формулы вычисления объема информации I = N * k и подсчета количества вариантов Q=M k взаимодействуют друг с другом через величину k (бит на символ).

Алфавитный подход к измерению информации

Основные понятия и термины:

Алфавит – это набор символов, используемых в языке, на котором передается сообщение. При этом символом алфавита могут быть буквы, цифры и прочие символы, входящие в сообщение.

Мощность алфавита — это количество символов в алфавите.

Например, мощность русского алфавита равна 32 при Е =Ё и 33 – в противном случае. Мощность английского алфавита равно 26.0

Для упрощения понимания и легкости запоминания различий в рассматриваемых далее задачах, разобьем их на 5 типов и будем рассматривать решения соответственно этим типам.

Для быстрого и точного вычисления количества информации следует применять таблицу степеней двойки, которая показывает, сколько вариантов всевозможных «слов» Q можно закодировать с помощью k бит на символ.

Так же при решении задач следует обязательно привести единицы измерения количества информации к одному виду. При этом помним, что значение k – это бит на символ, другого измерения здесь быть не может!

Задача 1 типа.

В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена.

Каков информационный объем в битах сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов?

Рекомендации к решению.

Перед решением этой задачи следует проговорить ее условие, заменяя слова из него синонимами, которые можно найти в формулах.

Читаем условие очень внимательно, находим хотя бы один синоним – и задача практически решена, остается только подставить формулы и получить ответ!

Чтобы легче запомнить задачи 1 типа, будем называть их общим термином «велосипедисты».

Есть 119 спортсменов с различными номерами, т.е. 119 вариантов различных номеров, тогда Q=119.

Так как Q = М k , то для одного номера получаем Q = 119 ≤ 128=27, откуда k=7.

Тогда для N = 70 номеров получаем информационный объем сообщения

I = N * k = 70 * 7 = 490 бит.

Также для вычисления значения бита на символ можно использовать математическое решение формулы Хартли:

В данном случае k= log₂8 = 3.

Задача 2 типа.

Объем сообщения, содержащего 4096 символов, равен 1/512 части Мбайт. Какова мощность алфавита, с помощью которого записано это сообщение?

Рекомендации к решению.

Задачи данного типа – чисто математические (так и запомним их определение), и здесь очень полезно использовать таблицы степеней двойки и соответствия единиц измерения количества информации.

Подставляем числовые значения в формулы, заменяем числа степенями числа 2 и упрощаем. При этом не забываем привести единицы измерения к одному виду и помнить, что k – это бит на символ!

Воспользовавшись таблицей степеней двойки, имеем: N = 4096 = 212 символов, тогда I =1/512 Мбайта = 223/29=214 бит. Отсюда k = I/N = 214/212=22=4 бита на символ.

Тогда мощность алфавита (количество различных вариантов символов)

М=24 = 16 символов.

Задача 3 типа.

В некоторой стране автомобильный номер длиной 7 символов составляется из заглавных букв (всего используется 26 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт.

Определите объем памяти, необходимый для хранения 20 автомобильных номеров.

Рекомендации к решению.

Решая задачи данного типа, необходимо обратить внимание на слова «каждый символ» и «каждый номер», которыеподразумевают разделение информации при решении. Поэтому при решении задач 3 типа следует сначала считать объем одного номера в битах, перевести его в байты (с округлением до целого числа в большую сторону!) и только потом искать общий объем на несколько номеров.

Округление в большую сторону при вычислении объема одного номера необходимо, чтобы не потерять ни одного символа кодируемой информации.

Запомним, что округление при вычислении объемов информации всегда будем выполнять в большую сторону!

Будем так и называть этот тип задач – «автомобильные номера», хотя здесь встречаются и задачи на нахождение паролей (решение задач от этого не зависит).

Особенность решения данной задачи – решение в два шага, т.е. поиск двух видов объема:

Шаг 1. Мощность используемого алфавита Q = 26 + 10 = 36 ≤26, откуда k=6 бит на символ. Тогда I1 = 7*6=42 бита = > 6 байт на один номер.

Шаг 2.Следовательно, на 20 номеров требуется I2 = 20 * 6 = 120 байт.

Для проверки правильности рассуждений пересчитаем объем без учета рекомендаций, данных ранее, и сравним итоги.

Мощность используемого алфавита и значение k=6 бит на символ остаются. Тогда объем одного номера I₁ = 7*6=42 бита, а 20 номеров I₂ = 42 * 20 = 840 бит > = 105 байт.

В итоге потеряны 15 байт информации, а это значит, что не все номера были бы закодированы.

Задача 4 типа.

В школьной базе данных хранятся записи, содержащие информацию об учениках:

Каждое поле записывается с использованием минимально возможного количества бит. Определите минимальное количество байт, необходимое для кодирования одной записи, если буквы е и ё считаются совпадающими.

Рекомендации к решению.

Перед решением задач данного типа вспомним, что базы данных (далее – БД) состоят из записей, которые делятся на поля.

И преимущество БД перед другим способом хранения информации в том, что поля в одной записи могут иметь разные форматы данных(числовые, символьные, даты и др.), которые кодируются соответственно их форматам.

Поэтому для подсчета общего объема одной записи следует считать объем каждого поля отдельно, а затем сложить их.

При этом помним, что в таблице ASCII (так как таблица кодировки в условии задачи не указана, берем ее по умолчанию) каждый символ занимает один байт памяти. Число (до определенного значения) – тоже кодируется одним байтом памяти.

Запомним определение задач 4 типа как «базы данных».

Определяем минимально возможные размеры в битах для каждого из полей (в данном случае – четырех) с учетом их типов отдельно.
Так как по условию задачи первые буквы имени, отчества и фамилии – всегда заглавные, то будем хранить их в виде строчных и делать заглавными только при выводе на экран.

Таким образом, для символьных полей достаточно использовать алфавит из 32 символов (русские строчные буквы, «е» и «ё» совпадают, пробелы не нужны).

Для кодирования каждого символа 32-символьного алфавита нужно 5 бит (32 = 25), то для хранения имени, отчества и фамилии нужно (16 + 12 + 16)•5=220 бит.

Для года рождения есть 12 вариантов чисел, поэтому для него нужно отвести 4 бита

Таким образом, всего требуется 220+4 = 224 бита или 28 байт.

Задача 5 типа (1).

В зоопарке 32 обезьяны живут в двух вольерах, А и Б. Одна из обезьян заболела. Сообщение «Заболевшая обезьяна живет в вольере А» содержит 4 бита информации.

Сколько обезьян живут в вольере Б?

Рекомендации к решению.

Заметим, что условие этой задачи отличается от задачи 1 типа только тем, что там все номера считались как единая информация, а здесь требуется выбор мотка определенного цвета, т.е. вся информация разделена на части.

По условию, красные клубки составляют 1/8 часть от целого (от всех клубков).

Поэтому сообщение о том, что первый вынутый клубок шерсти – красный, соответствует выбору одного из 8 вариантов, и это будет: Q = 8 = 23, что дает нам k = 3 бит.

(Можно запомнить решение задач 5 типа без дробей и дополнительных объяснений: в дополнительном по отношению к задачам 1 типа шаге находим Q = 32/4 = 8 вариантов, а затем решаем, как и задачи 1 типа: Q = 8 = 23, что дает нам k = 3 бит).

Задача 5 типа (2).

В зоопарке 32 обезьяны живут в двух вольерах, А и Б. Одна из обезьян заболела. Сообщение «Заболевшая обезьяна живет в вольере А» содержит 4 бита информации.

Сколько обезьян живут в вольере Б?

Почему эта задача относится к 5 типу? Потому что информация разделена на части – обезьяны здоровые и больные.

Решается она в порядке, обратном решению предыдущей задачи.

Итак, информация в 4 бита соответствует выбору одного из 16 вариантов, поэтому в вольере А живет 1/16 часть всех обезьян: 32/16 = 2 обезьяны

Тогда в вольере Б живут все оставшиеся 32 – 2 = 30 обезьян.

Описание задач 5 типа можно определить и запомнить как задачи «про шары и обезьян».

Задачи смешанных типов.

Усвоив решение каждого типа задач отдельно, можно рассмотреть задачи смешанных типов.

Для их успешного решения необходимо прежде всего внимательно рассмотреть условие задачи, чтобы не пропустить это смешивание, а потом уже решать с учетом всех тонкостей, описанных ранее.

Разберем две из таких задач.

Задача 1.

При регистрации в компьютерной системе каждому пользователю выдаётся идентификатор, состоящий из 8 символов, первый и последний из которых – одна из 18 букв, а остальные – цифры (допускается использование 10 десятичных цифр.

Каждый такой идентификатор в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование; все цифры кодируются одинаковым и минимально возможным количеством бит, все буквы также кодируются одинаковым и минимально возможным количеством бит).

Определите объём памяти в байтах, отводимый этой программой для записи 500 паролей.

Рассмотрим условие и разделим его на части, относящиеся к разным типам задач.

В первом абзаце говорится, что идентификатор состоит из букв и цифр в определенном порядке, а они кодируются по-разному. Это подтверждается и во-втором абзаце, где способ кодировки для цифр и букв описывается отдельно. Следовательно, каждый идентификатор рассматривается как запись из БД, то есть эта часть задачи относится к типу 4.

Во втором абзаце условия так же сказано, что каждый идентификатор записывается минимально возможным и одинаковым целым количеством байт, а посимвольное (т.е. для каждого символа отдельно) кодирование выполняется минимальным количеством бит для каждого вида символов. Следовательно, эта часть задачи относится к типу 3.

Тогда решение будет следующим:

В идентификаторе шесть цифр из алфавита мощностью 10 символов.

Тогда k₁=4 и I1=6*k₁=24 бита.

Вторая часть идентификатора длиной 2 символа состоит из алфавита мощностью 18 символов. Тогда k₂=5 и I₂=2*k2=10 бит.
Значит, объем одного идентификатора равен I₁ + I₂ = 24 + 10 = 34 бита.

Далее решаем задачу соответственно решению, описанному в 3 типе задач:

34 бита = 5 байт,

Общий объем 500 идентификаторов равен I = 5*500=2500 байт.

Задача 2.

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит.

Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт на одного пользователя.

Определите объём памяти (в байтах), необходимый для хранения сведений о 50 пользователях. В ответе запишите только целое число – количество байт.

В условии сказано, что сведения о пользователях хранятся в БД, где запись состоит из двух полей – собственно идентификатора и дополнительных сведений (тип 4).

При этом идентификатор рассчитывается как в задачах 1 типа, а дополнительные сведения заданы конкретным значением и расчет их не нужен.

Тогда решение будет следующим:

Мощность используемого алфавита Q = 12 ≤24, откуда k=4 бита на символ. Тогда I₁ = 15*4 = 60 бит >= 8 байт на один идентификатор.

Объем одной записи равен I₁+2 = 8 + 12 = 20 байт.

Следовательно, для 50 записей требуется I50 = 20 * 50 = 1000 байт.

Источник

• ← Какой что это такое простыми словами
• Какой шанс того что девушка забеременеет →