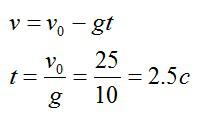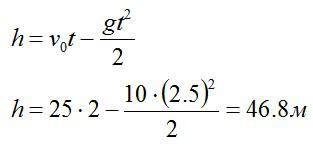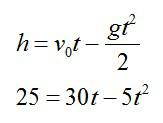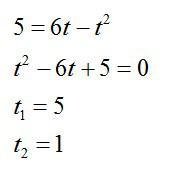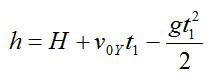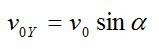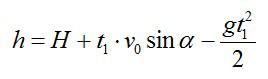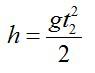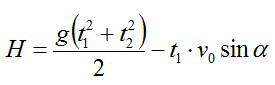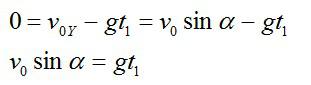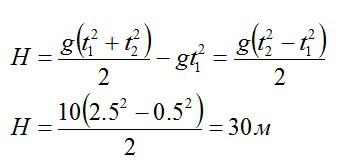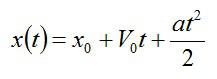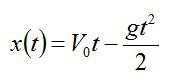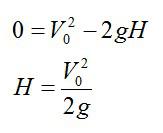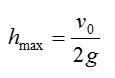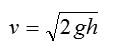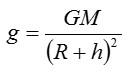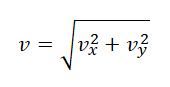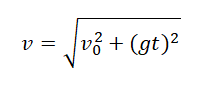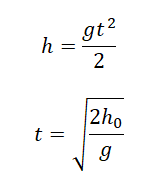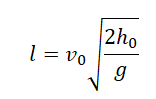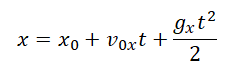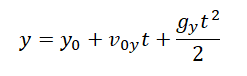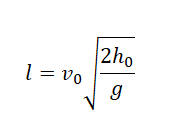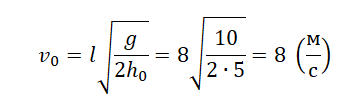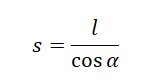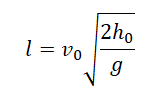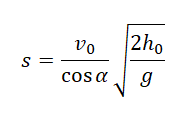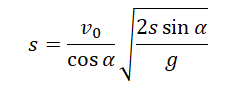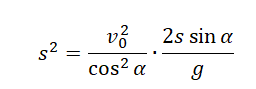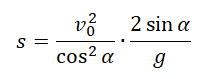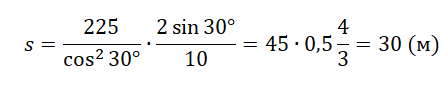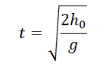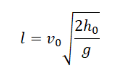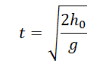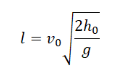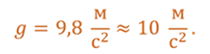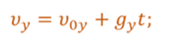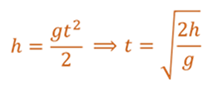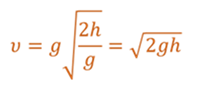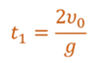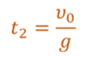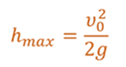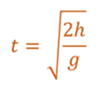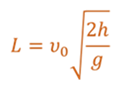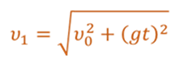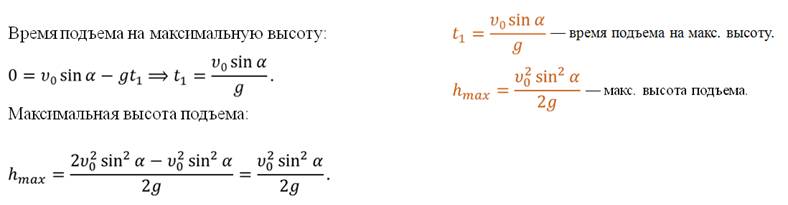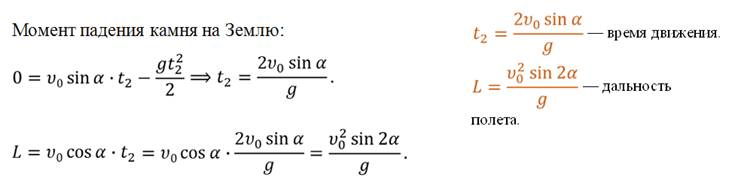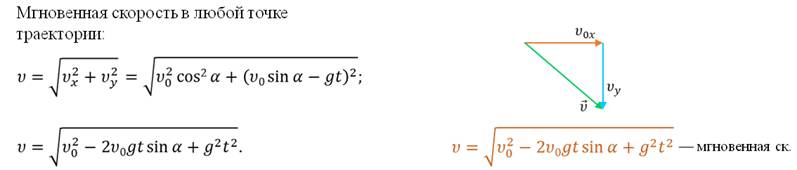Камень свободно падает что происходит при этом с весом камня

Задачи на свободное падение тел: примеры решения задач по кинематике

Вторник, а это значит, что сегодня мы снова решаем задачи. На это раз, на тему «свободное падение тел».

Присоединяйтесь к нам в телеграм и получайте актуальную рассылку каждый день!

Задачи на свободное падение тел с решением

Задача №1. Нахождение скорости при свободном падении

Условие

Тело падает с высоты 20 метров. Какую скорость оно разовьет перед столкновением с Землей?

Решение

Высота нам известна по условию. Для решения применим формулу для скорости тела в момент падения и вычислим:

Ответ: примерно 20 метров в секунду.

Задача №2. Нахождение высоты и времени движения тела, брошенного вертикально.

Условие

Индеец выпускает стрелу из лука вертикально вверх с начальной скоростью 25 метров в секунду. За какое время стрела окажется в наивысшей точке и какой максимальной высоты она достигнет стрела?

Решение

Сначала запишем формулу из кинематики для скорости. Как известно, в наивысшей точке траектории скорость стрелы равна нулю:

Теперь запишем закон движения для вертикальной оси, направленной вертикально вверх.

Ответ: 2,5 секунды, 46 метров.

Задача №3. Нахождение времени движения тела, брошенного вертикально вверх

Условие

Мячик бросили вертикально вверх с начальной скоростью 30 метров в секунду. Через какое время мяч окажется на высоте 25 метров?

Решение

Запишем уравнение для движения мячика:

Мы получили квадратное уравнение. Упростим его и найдем корни:

Как видим, уравнение имеет два решения. Первый раз мячик побывал на высоте через 1 секунду (когда поднимался), а второй раз через 5 секунд (когда падал обратно).

Ответ: 1с, 5с.

Задача №4. Нахождение высоты при движении тела под углом к горизонту

Условие

Камень, брошенный с крыши дома под углом альфа к горизонту, через время t1=0,5c достиг максимальной высоты, а еще через время t2=2,5c упал на землю. Определите высоту Н дома. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.

Решение

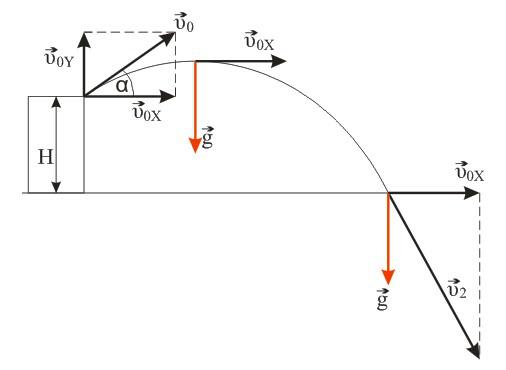
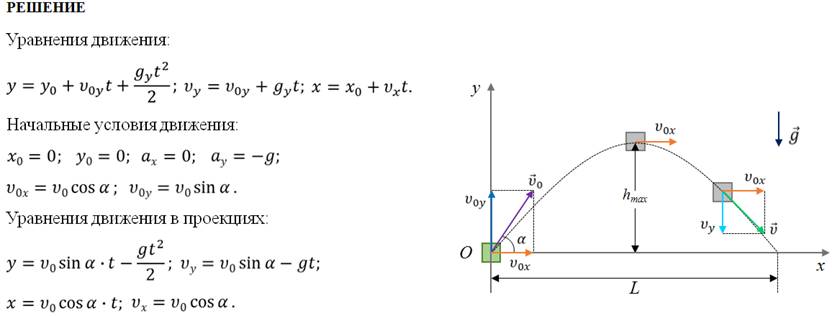
Камень брошен со скоростью v0 под углом α к горизонту с дома высотой Н. Эту скорость можно разложить на две составляющие: v0X (горизонтальная) и v0Y (вертикальная). В горизонтальном направлении на камень не действует никаких сил (сопротивлением воздуха пренебрегаем), поэтому горизонтальная составляющая скорости неизменна на протяжении всего времени полета камня (равномерное движение). Максимальная точка траектории камня над уровнем земли (исходя из кинематических соотношений):

Здесь t1 – время подъема камня с высоты Н на высоту h; g – ускорение свободного падения.

Вертикальную составляющую скорости можно вычислить исходя из геометрических соображений:

Подставив выражение для скорости в первое уравнение, получим:

Также высоту h можно выразить через время t2 падения камня с высоты h на землю (исходя из кинематических соотношений и учитывая, что с вертикальная составляющая скорости в наивысшей точке равна нулю):

Для высоты дома можно записать:

Так как вертикальная составляющая скорости камня в максимальной точке траектории равна нулю:

Подставляем в формулу для высоты H и вычисляем:

Ответ: H = 30 м.

Задача №5. Нахождение закона движения тела

Условие

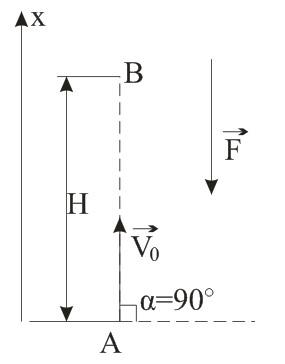
Найти закон движения тела против силы тяжести, при начальной скорости V0. И на какую максимальную высоту поднимется тело? Тело бросили под углом 90 градусов.

Решение

Тело брошено под углом α=90° к горизонту. Другими словами, тело брошено вертикально вверх с начальной скоростью V0. Направим координатную ось х вертикально вверх, так ее направление совпадает с вектором начальной скорости. F – сила тяжести, направленная вниз. В начальный момент тело находится в точке А.

В задаче нужно найти закон движения тела, то есть зависимость координаты тела от времени. В общем случае этот закон задается кинематическим соотношением:

где х0 – начальная координата тела; a – ускорение.

Так как мы поместили начало координат в точку А, х0=0. Тело движется с ускорением свободного падения g, при этом сила тяжести направлена против начальной скорости, поэтому в проекции на вертикальную ось a=-g. Таким образом, искомый закон движения перепишется в виде:

Далее будем использовать еще одно общее кинематическое соотношение:

где V – конечная скорость.

Максимальная высота подъема тела указана на рисунке точной B, в этот момент конечная скорость V равна нулю, а координата х равна максимальной высоте Н подъема тела. Отсюда можно найти выражение для этой величины:

Полезные формулы для решения задач на свободное падение

Свободное падение описывается формулами кинематики. Мы не будем приводить их вывод, но запишем самые полезные.

Формула для максимальной высоты подъема тела, брошенного вертикально вверх c некоторой начальной скоростью:

Кстати, как выводится именно эта формула можно посмотреть в последней задаче.

Формула для времени подъема и падения тела, брошенного вертикально вверх:

Скорость тела в момент падения с высоты h:

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Вопросы с ответами на свободное падение тел

Вопрос 1. Как направлен вектор ускорения свободного падения?

Ответ: можно просто сказать, что ускорение g направлено вниз. На самом деле, если говорить точнее, ускорение свободного падения направлено к центру Земли.

Вопрос 2. От чего зависит ускорение свободного падения?

Ответ: на Земле ускорение свободного падения зависит от географической широты, а также от высоты h подъема тела над поверхностью. На других планетах эта величина зависит от массы M и радиус R небесного тела. Общая формула для ускорения свободного падения:

Вопрос 3. Тело бросают вертикально вверх. Как можно охарактеризовать это движение?

Ответ: В этом случае тело движется равноускоренно. Причем время подъема и время падения тела с максимальной высоты равны.

Вопрос 4. А если тело бросают не вверх, а горизонтально или под углом к горизонту. Какое это движение?

Ответ: можно сказать, что это тоже свободное падение. В данном случае движение нужно рассматривать относительно двух осей: вертикальной и горизонтальной. Относительно горизонтальной оси тело движется равномерно, а относительно вертикальной – равноускоренно с ускорением g.

Баллистика – наука, изучающая особенности и законы движения тел, брошенных под углом к горизонту.

Вопрос 5. Что значит «свободное» падение.

Ответ: в данном контексте понимается, что тело при падении свободно от сопротивления воздуха.

Свободное падение тел: определения, примеры

Свободное падение – равноускоренное движение, происходящее под действием силы тяжести.

Первые попытки систематизированно и количественно описать свободное падение тел относятся к средневековью. Правда, тогда было широко распространено заблуждение, что тела разной массы падают с разной скоростью. На самом деле, в этом есть доля правды, ведь в реальном мире на скорость падения сильно влияет сопротивление воздуха.

Однако, если им можно пренебречь, то скорость падающих тел разной массы будет одинакова. Кстати, скорость при свободном падении возрастает пропорционально времени падения.

Ускорение свободно падающих тел не зависит от их массы.

Примеры свободного падения тел:

При свободном падении тела возникает состояние невесомости. Например, в таком же состоянии находятся предметы на космической станции, движущейся по орбите вокруг Земли. Можно сказать, что станция медленно, очень медленно падает на планету.

Конечно, свободное падение возможно не только не Земле, но и вблизи любого тела, обладающего достаточной массой. На других комических телах падения также будет равноускоренным, но величина ускорения свободного падения будет отличаться от земной. Кстати, раньше у нас уже выходил материал про гравитацию.

При решении задач ускорение g принято считать равным 9,81 м/с^2. В реальности его величина варьируется от 9,832 (на полюсах) до 9,78 (на экваторе). Такая разница обусловлена вращением Земли вокруг своей оси.

Нужна помощь в решении задач по физике? Обращайтесь в профессиональный студенческий сервис в любое время.

Источник

Движение тела, брошенного горизонтально

теория по физике 🧲 кинематика

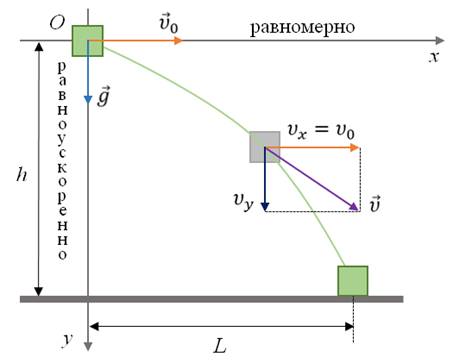
Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.

Кинематические характеристики движения

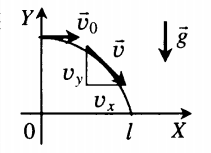
Графически движение горизонтально брошенного тела описывается следующим образом:

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:

Минимальная скорость в течение всего времени движения равна начальной скорости: v_min = v₀.

Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: v_max = v.

Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:

h₀ — высота, с которой тело бросили в горизонтальном направлении.

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид :

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?

Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:

Выразим начальную скорость и вычислим ее:

Горизонтальный бросок тела с горы

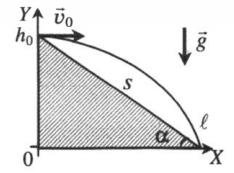
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.

График горизонтального броска тела с горы

α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения

Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:

Начальная высота — высота, с которой было брошено тело. Обозначается h₀. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:

Пример №2. На горе с углом наклона 30 о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?

Выразим это расстояние через дальность полета:

Дальность полета выражается по формуле:

Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:

Выразим с учетом формулы начальной высоты:

Поделим обе части выражения на общий множитель s:

Подставим известные значения:

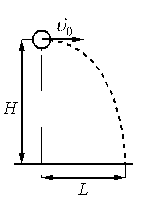
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ ₀, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).

В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2 υ ₀.

Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Время полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.

Дальность полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.

Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.

Значит, верный ответ — 313.

pазбирался: Алиса Никитина | обсудить разбор | оценить

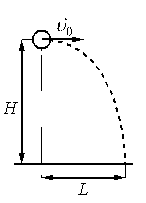
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ ₀, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).

Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Время полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.

Дальность полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).

Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.

Значит, верный ответ — 323.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Свободное падение. Ускорение свободного падения

Урок 7. Подготовка к ЕГЭ по физике. Часть 1. Механика.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Свободное падение. Ускорение свободного падения»

В данной теме разговор пойдёт о свободном падении тел, также поговорим об ускорении свободного падения и рассмотрим виды движений тел под действием силы тяжести.

Ранее говорилось о прямолинейном равноускоренном движении тел. Прямолинейное равноускоренное движение – это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, то есть это движение с постоянным по модулю и направлению ускорением. Ускорение — это векторная физическая величина, равная отношению изменения скорости к промежутку времени, в течении которого это изменение произошло.

Одно из наиболее распространенных видов движения с постоянным ускорением — это свободное падение тел.

Под свободным падением тела понимают движение тела только под действием силы тяжести.

Долгое время считалось, что ускорение, с которым падает тело, зависит от размеров и массы этого тела. Действительно, можно с уверенностью сказать, что листок с дерева или птичье перо падают значительно медленнее, чем камень или мяч, например.

Аристотель в свое время говорил, что «точно так же, как направленное вниз движение куска свинца или золота, или любого другого тела, наделенного весом, происходит тем быстрее, чем больше его размер». А «одно тело будет тяжелее другого, имеющего тот же объем, если оно движется вниз быстрее».

Вывод о том, что все тела, независимо от их масс, форм и размеров, совершают свободное падение совершенно одинаково, на первый взгляд может показаться противоречащим повседневному опыту.

Люди привыкли к тому, что тяжелые тела достигают земли быстрее, чем легкие, падающие с той же высоты. На самом деле никакого противоречия здесь нет. Известно, что дело здесь в том, что существует сила сопротивления воздуха, которая и препятствует свободному падению. В большинстве случаев эта сила незначительна, и ею можно пренебречь, за исключением тех случаев, когда сила сопротивления воздуха становится сравнимой с силой тяжести. Поэтому в дальнейшем будем рассматривать примеры, в которых силой сопротивления воздуха можно пренебречь.

Впервые предположение о том, что все тела падают с одинаковым ускорением, высказал Галилео Галилей. Опытным путем он доказал, что это предположение верно. Галилей провел один из самых знаменитых физических экспериментов: он сбросил с Пизанской башни ядро и мушкетную пулю на глазах у многих людей. Вопреки ожиданиям, и ядро, и пуля упали одновременно.

Исаак Ньютон провел иной опыт, чтобы ещё раз доказать справедливость предположения Галилея. Он поместил в стеклянную трубку дробинки, кусочки пробки и пушинку. Перевернув трубку, он наблюдал, как сначала упали дробинки, потом кусочки пробки и только потом пушинка. Затем он откачал из трубки воздух и повторил эксперимент. Как и ожидалось, все тела упали одновременно. Это свидетельствует о том, что ускорение свободного падения постоянно для любого тела, а различные скорости падения могут быть обусловлены сопротивлением воздуха.

Таким образом, в данном месте Земли все тела, независимо от их массы и других физических характеристик, совершают свободное падение с одинаковым ускорением — ускорением свободного падения. Обозначается оно малой латинской буквой g. Его значение вблизи поверхности Земли не постоянно и варьируется от 9,78 м/с 2 на экваторе до 9,83 м/с 2 – на полюсах.

Стандартное значение ускорения свободного падения было определено как «среднее» в каком-то смысле на всей Земле, оно примерно равно ускорению свободного падения на широте 45,5º на уровне моря. В приблизительных расчётах его обычно принимают равным

Однако следует помнить о том, что данным значением ускорения свободного падения можно пользоваться только для вычислений, когда тело движется вблизи поверхности Земли. Все дело в том, что в соответствии с законом всемирного тяготения, ускорение свободного падения зависит и от массы планеты, и от ее радиуса, и от высоты над поверхностью планеты.

Ускорение свободного падения в данной точке земного шара всегда направлено вертикально вниз к центру Земли.

Рассмотрим свободное падение тел по прямолинейной и криволинейной траекториям. Сразу обратим внимание на то, что во всех случаях, которые будут рассматриваться, движение тела будет описываться двумя основными уравнениями равноускоренного движения — уравнением скорости и кинематическим уравнением равноускоренного движения.

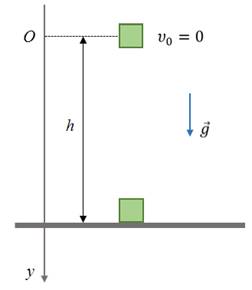
Рассмотрим тело, которое свободно падает без начальной скорости с некоторой высоты h над поверхностью Земли.

В этом случае все время полета можно определить из кинематического уравнения для равноускоренного движения.

Если данное значение промежутка времени подставить в уравнение скорости для равноускоренного движения, то можно легко получить формулу для расчета скорости в последний момент движения.

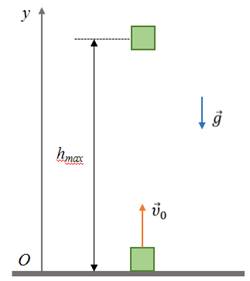
Следующим вспомним движение тела, брошенного вертикально вверх с некоторой начальной скоростью.

При таком движении время всего полета определяется формулой:

А время подъема тела на максимальную высоту в два раза меньше всего времени движения.

Максимальную высоту подъема не трудно определить из уравнения перемещения для равноускоренного движения, зная время подъема тела и то, что в верхней точке траектории скорость тела обращается в ноль.

Что касается скорости тела в последний момент движения, то оказывается, что с какой скоростью тело брошено вертикально вверх, с такой же по модулю скоростью оно вернется обратно.

Рассмотрим падения тел по криволинейной траектории. Такое движение возникает в том случае, если вектор начальной скорости тела направлен не вертикально вверх.

Начнем с рассмотрения движения тела, брошенного в горизонтальном направлении с некоторой высоты и начальной скоростью.

При рассмотрении такого движения используется две координатные оси, так как движение происходит в двух плоскостях.

Главное помнить о том, что в горизонтальном направлении тело движется равномерно, а вот движение в вертикальной плоскости — равноускоренное, то есть в вертикальной плоскости тело движется также, как и при свободном падении без начальной скорости.

Зная высоту, с которой брошено тело, можно определить время всего движения

Как видно, время падения не зависит от начальной скорости тела и это время равно времени свободного падения тела с некоторой высоты без начальной скорости. За это время тело в горизонтальном направлении пройдет некоторое расстояние, которое называют дальностью полета, при этом чем больше начальная скорость, тем большая дальность полета тела.

Мгновенную скорость тела в любой момент времени можно рассчитать по формуле:

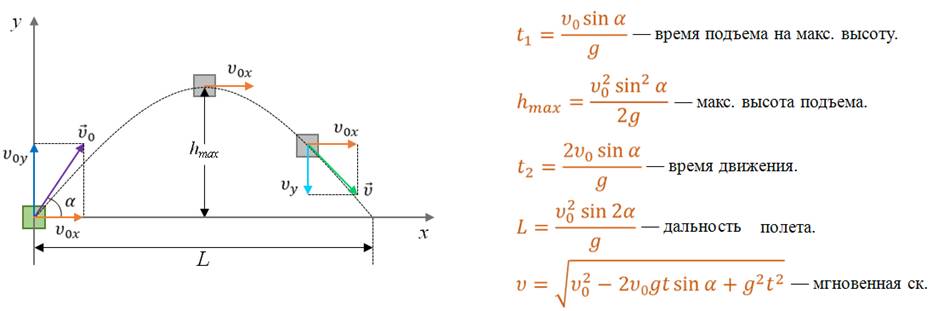
Рассмотрим последний вид движения под действием силы тяжести — движение тела, брошенного под углом к горизонту. Для этого решим следующую задачу.

Задача. Камень бросили под углом α к горизонту с начальной скоростью υ₀. Определите: скорость и координаты камня через время t после бросания, время полета, максимальную высоту, на которую поднимется тело, дальность полета и скорость тела в момент падения на Землю. Сопротивлением воздуха пренебречь.

Таким образом, для движения тела, брошенного под углом к горизонту

Было рассмотрено свободное падение тел. Ускорение, с которым движется тело во время свободного падения, называют ускорением свободного падения. Были рассмотрены виды наиболее часто встречающихся движений тел под действием силы тяжести — это свободное падение тел по прямолинейной и криволинейной траектории.

Источник