Квадратная рамка с током закреплена так что может свободно вращаться вокруг
Ниже приведены условия задач и отсканированные листы с решениями. Загрузка страницы может занять некоторое время.
409. По двум бесконечно длинным, прямым параллельным проводам текут одинаковые токи I=60 А. Определить магнитную индукцию B в точке B (рис.), рав-ноудаленной от проводов на расстояние L=10см. Угол β = π/3.
419. Квадратная рамка из тонкого провода может свободно вращаться вокруг горизонтальной оси, совпадающей с одной из сторон. Масса m рамки равна 20 г. Рамку поместили в однородное магнитное поле (В= 0,1 Тл), направленное вертикально вверх. Определить угол φ, на который отклонилась рамка от вертикали, когда по ней пропустили ток I= 10 А.
429. По поверхности диска радиусом R=15 см равномерно распределен заряд σ = 0,2мкКл. Диск вращается с угловой скоростью ω = 30 рад/с относительно оси, перпендикулярной плоскости диска и проходящей через его центр. Определить магнитный момент Pm, обусловленный вращением диска.
439. Ион с кинетической энергией E= 1 кэВ попал в однородное магнитное поле (В = 21 мТл) и стал двигаться по окружности. Определить магнитный момент Pm эквивалентного кругового тока.
449. Магнитное (В = 2мТл) и электрическое (Е = 1,6кВ/м) поля сонаправлены. Перпендикулярно векторам В и Е влетает электрон со скоростью V = 0,8 Мм/с. Определить ускорение а электрона.
459. Плоский контур с током I=50 А расположен в однородном магнитном поле (В = 0,6Тл) так, что нормаль к контуру перпендикулярна линиям магнитной индукции. Определить работу, совершаемую силами поля при медленном повороте контура около оси, лежащей в плоскости контура, на угол φ=30°.
469. Проволочный контур площадью S = 500 см2 и сопротивлением R = 0,1 Ом равномерно вращается в одно¬родном магнитном поле (В = 0,5 Тл). Ось вращения лежит в плоскости кольца и перпендикулярна линиям магнитной индукции. Определить максимальную мощность Рmах, необходимую для вращения контура с угловой скоростью ω = 50 рад/с.
479. Источник тока замкнули на катушку сопротивлением R =10 Ом и индуктивностью L=0,2 Гн. Через сколько времени сила тока в цепи достигнет 50% максимального значения?
Еще примеры решения задач по физике можно бесплатно скачать здесь.
При расчете потока вектора магнитной индукции следует обращать внимание на то, какое рассматривается поле: однородное или неоднородное. Для однородного поля
где S – площадь поверхности;
Для неоднородного поля ФВ вычисляется через поверхностный ин-теграл:
. (60)
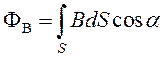
При перемещении контура с током в магнитном поле совершается работа, которая зависит от приращения магнитного потока через плоскость, ограниченную проводником:
(61)
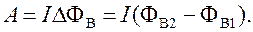
Примеры решения задач
Задача 7. Круговой контур радиусом 30 см находится в однородном магнитном поле с индукций 0,3 Тл так, что его плоскость составляет угол 60° с линиями магнитной индукции. Найти значение магнитного потока, пронизывающего контур.
Решение.
В случае однородного магнитного поля (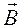 
= const) поток вектора магнитной индукции
Площадь кругового витка определим по формуле:
Величину угла a между нормалью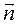 
и вектором магнитной индукции найдем из рис. 17:
Подставим формулу (63) в выражение (62), получим расчетное уравнение:
Рассчитаем поток вектора магнитной индукция, подставив данные задачи в формулу (64):
Задача 8. Квадратный контур с током 5 А свободно установился в однородном магнитном поле с индукцией 50 мТл. Сторона квадрата равна 10 см. Поддерживая ток неизменным, контур повернули относительно оси, лежащей в плоскости контура и перпендикулярной линиям индукции, на угол 90°. Определить совершенную при этом работу.
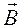
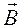
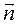
Квадратная рамка с током I свободно установилась в магнитном поле (рис. 18, а). Вектор перпендикулярен плоскости рамки и совпадает по направлению с вектором нормали (a1 = 0).
Работа внешних сил при повороте рамки на 90° (рис. 18, б) равна работе сил поля, взятой с противоположным знаком:
А = –Ам.п =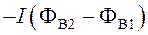 
, (65)
В случае однородного магнитного поля магнитный поток:
Площадь квадратного контура определим по формуле:
Подставим выражения (66), (67) в уравнение (65) и получим расчетную формулу:
. (68)
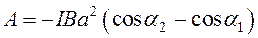
Рассчитаем работу внешних сил, подставив данные задачи в формулу (68):
Задача 9. В одной плоскости с бесконечно длинным прямым проводом, по которому идет ток 5 А, расположена квадратная рамка со стороной а, равной 5 см, обтекаемая током 0,5 А. Ближайшая сторона рамки параллельна прямому току и находится от него на расстоянии b, равном 8 см. Определить работу, которую надо совершить, чтобы повернуть рамку на 180 о вокруг дальней стороны рамки. Токи в проводнике и ближней стороне рамки в начальный момент времени направлены в одну сторону.
Большая Энциклопедия Нефти и Газа
Квадратная рамка
Квадратная рамка из медной проволоки, площадь которой 25 см2, помещена в магнитное поле с индукцией 0 1 Тл. Нормаль к рамке параллельна вектору магнитной индукции поля. [31]
Квадратная рамка со стороной 5 см, имеющая 10 витков, находится в однородном магнитном поле с индукцией 0 1 Тл. Плоскость рамки составляет угол 0 с направлением магнитного поля. Определить вращающий момент сил, действующих на рамку, если ток в рамке равен 4 А. [32]
Квадратную рамку Р ( рис. 4.2) размером 5X5 см вращают в однородном магнитном поле с индукцией В 0 1 Тл, с угловой скоростью ш 62 8 1 / с. [35]
По квадратной рамке со стороной 0 2м течет ток 4 А. [39]
О 9.1.6. Квадратная рамка с током закреплена так, что может свободно вращаться вокруг горизонтально расположенной стороны. Рамка находится в вертикальном однородном магнитном поле индукции В. [40]
О 9.1.6. Квадратная рамка с током закреплена так, что может свободно вращаться вокруг горизонтально расположенной стороны. [41]
1ОТл вращается квадратная рамка со стороной 6 см, имеющая 40 витков. [42]
В плоскости квадратной рамки с омическим сопротивлением R 7 Ом и стороной / 0 2 м расположен на расстоянии Г0 0 2 м от рамки прямой бесконечный проводник параллельно одной из сторон рамки. [43]
На графике квадратной рамкой отмечаются те часы работы, когда фактическое количество изготовленных деталей соответствовало плану или превышало плановое задание за отработанное с начала смены время. Это делает график более наглядным. [44]
А, расположена квадратная рамка с током / 22 00 А. [45]
Задача 1
Задача №3.1. В ОМП (В=0,02 Тл) в плоскости, перпендикулярной линиям индукции, расположено проволочное полукольцо (рис. ) длины l=3 см, по которому течет ток силы I=0,1 А. Найти результирующую силу, действующую на полукольцо. Изменится ли сила, если проводник распрямить? [38 мкН; увеличится в p/2 раз] (10, с. 242)
Указания по решению. 1) На элемент тока в магнитном поле действует сила (3.1):
,
направление которой определяется по правилу левой руки (рис. ). Силы Ампера, действующие на отдельные участки кольца лежат в одной плоскости (плоскости полукольца), т.е. имеют составляющие по 2-м осям х и у.
Результирующая сила, действующая на кольцо, согласно рис. стремиться растянуть его и находится как
,
и 
.
,
.
2) Если проводник распрямить, то становится применимой формула (3.3), тогда
,
т.е. сила увеличивается в 
раз.
Подумайте, чему будет равна сила Ампера в случае, когда полукольцо будет лежать в плоскости, параллельной силовым линиям заданного ОМП?
Задача 2
Квадратная рамка с током закреплена так, что может свободно вращаться вокруг горизонтально расположенной стороны. Рамка находится в вертикальном однородном магнитном поле индукции B. Угол наклона рамки к горизонту a, ее масса m, длина стороны a. Найдите ток в рамке. [ 
]
Указания по решению.
Т.к. рамка находится в равновесии, то алгебраическая сумма моментов всех сил, действующих на нее относительно оси вращения равен нулю:
,
,
Þ
Изобразите самостоятельно на рисунке все силы, действующие со стороны магнитного поля на каждую из сторон рамки. Найдите моменты этих сил относительно закрепленной стороны рамки.
Задача 3
Указания по решению.
При движении проводника с такой же скоростью перемещаются относительно магнитного поля и свободные электроны в нем. Тогда на отдельный свободный электрон действует сила Лоренца
.
Под ее действием свободные электроны смещаются к одному краю проводника, создавая на его концах разность потенциалов. Смещение электронов прекращается, когда сила Лоренца уравновешивается силой кулоновского отталкивания электронов. При этом уравниваются и значения работы по перемещению электронов для указанных сил:
Þ 
.
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)
Задание EF17725
На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
📜Теория для решения: Сила Ампера
Решение
Алгоритм решения
Решение
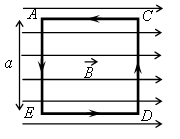
По условию задачи известными данными являются:
Пусть по рамке течёт ток I. На стороны АЕ и CD будут действовать силы Ампера:
F A 1 = F A 2 = I a B
Для того чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Момент силы Ампера относительно оси, проходящей через сторону CD:
Момент силы тяжести относительно оси CD:
Чтобы рамка с током оторвалась от горизонтальной поверхности, нужно чтобы суммарный момент сил был больше нуля:
Так как момент силы тяжести относительно оси CD отрицательный, это неравенство можно записать в виде:
Отсюда выразим силу тока:
Добавить комментарий Отменить ответ
Похожие задания:
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со.
На дне бассейна с водой находится небольшая лампочка. На поверхности воды.
Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей.
Период свободных электромагнитных колебаний в идеальном колебательном контуре.
В электрической цепи, показанной на рисунке, ключ К длительное время замкнут.
В электрической цепи, показанной на рисунке, ЭДС и внутреннее сопротивление.
На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС.
По горизонтально расположенным шероховатым рельсам с пренебрежимо малым.
Реостат R подключен к источнику тока с ЭДС E и внутренним сопротивлением r (см.
На рис. 1 изображена зависимость силы тока через светодиод D от приложенного к.
Протон влетает в электрическое поле конденсатора параллельно его пластинам в.
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на.