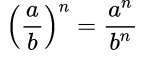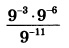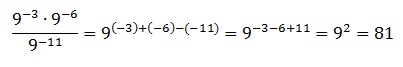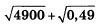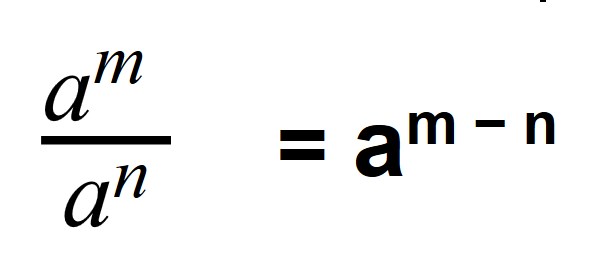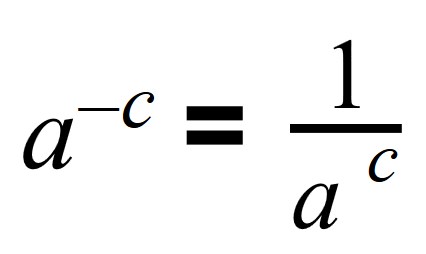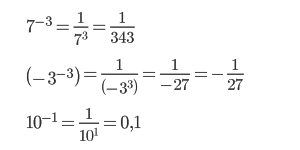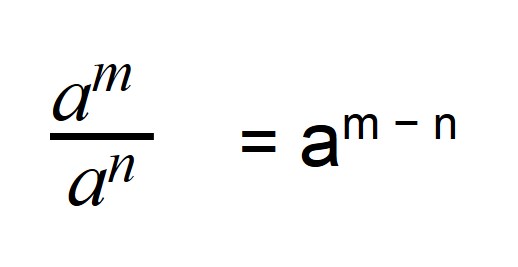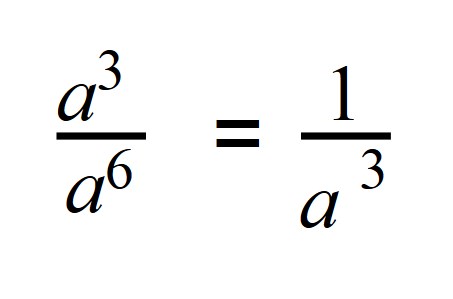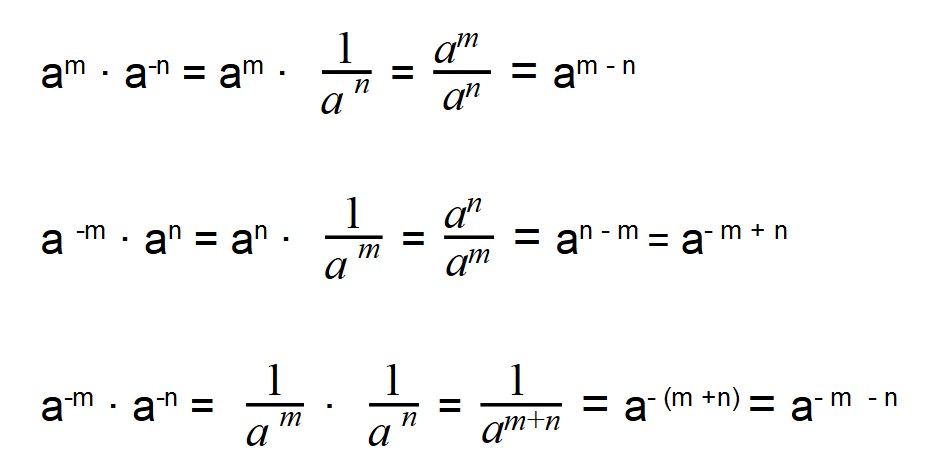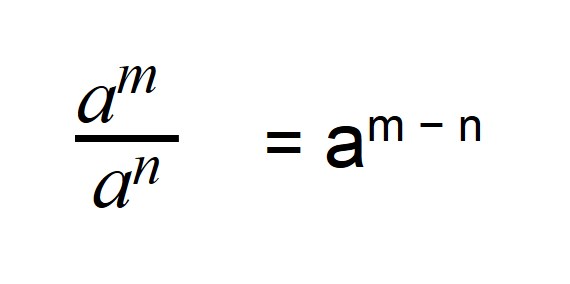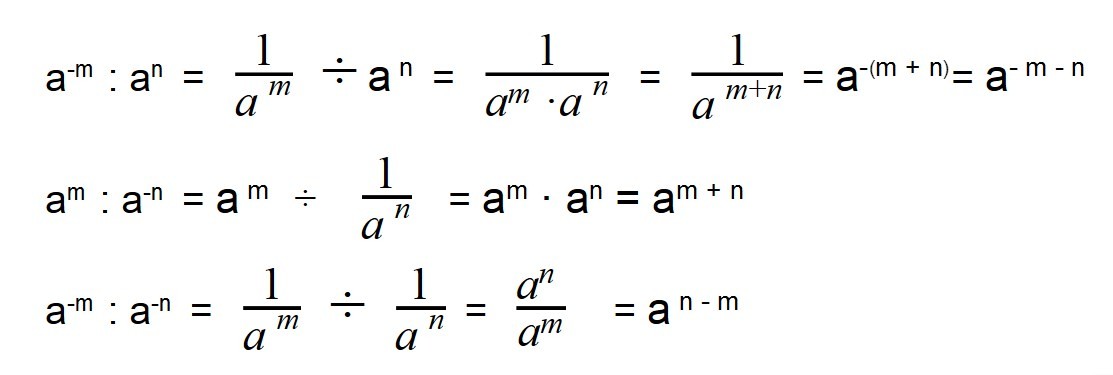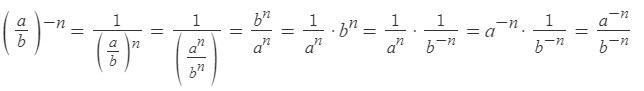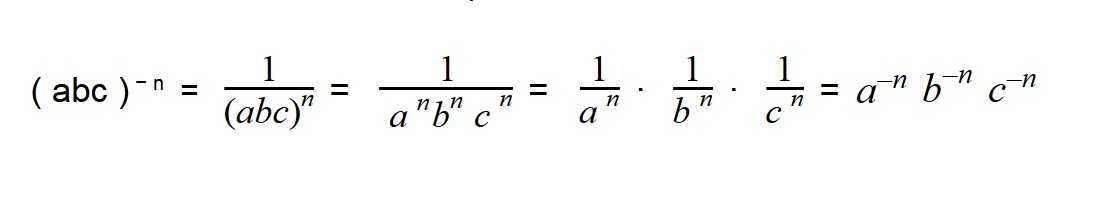При делении что делать со степенями при
Действия со степенями
теория по математике 📈 числа и вычисления
Степенью числа a с натуральным показателем n называют произведение n одинаковых множителей, каждый из которых равен а. То есть а n =a×a×a×a …..a (а берется n раз). Число а называют основанием, а число n показателем степени. Показатель показывает, сколько раз берется основание как множитель.
Свойства степени (применимы для степеней с одинаковым основанием)
При умножении степеней с одинаковым основанием основание оставляют тем же, а показатели складывают:
a n × a m =a n +m
5 5 ×5 3 ×5 4 =5 5+3+4 =5 12
При делении степеней с одинаковым основанием основание оставляют тем же, а показатели вычитают:
a n : a m =a n — m
с 12 :с 5 =с 12-5 = с 7
3 23 :3 20 =3 23-20 = 3 3
Возведение степени в степень
При возведении степени в степень основание оставляют тем же, а показатели умножают:
(a n ) m =a n×m
При возведении в степень произведения разных множителей необходимо возвести в эту степень каждый множитель:
(a×b×c) m =a m ×b m ×c m
(3 2 5 4 ) 6 =3 12 5 24
Степень дроби (степень частного)
При возведении в степень обыкновенной дроби необходимо возвести в данную степень числитель и знаменатель дроби:
Важные правила для работы со степенями
В числителе дроби возведем в степень каждый множитель:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Подставляем значение a = 13:
pазбирался: Даниил Романович | обсудить разбор | оценить
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5) 2 — x (x — 10) = x 2 + 2 • 5 • x + 25 — x 2 + 10x
Затем приведем подобные слагаемые:
x 2 + 2 • 5 • x + 25 — x 2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24
pазбирался: Даниил Романович | обсудить разбор | оценить
Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
pазбирался: Даниил Романович | обсудить разбор | оценить
Значение какого из выражений является рациональным числом?
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
Данный вариант ответа нам подходит.
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
Суммарно наши действия выглядят так:
pазбирался: Даниил Романович | обсудить разбор | оценить
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
121 • 11 n = 11 2 • 11 n
С учетом правила умножения, складываем степени:
Следовательно, нам подходит второй ответ.
pазбирался: Даниил Романович | обсудить разбор | оценить
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Свойства степеней. Действия со степенями
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
a — основание степени;
n — показатель степени.
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Правила умножения и деления степеней
Что представляют собой степенные выражения
Степенью n для числа а является произведение множителей, которые по величине равны а, взятое n раз.
здесь а представляет собой основание степени, n определяет ее показатель.
Таким образом, можно составить формулу:
Запись можно прочитать, как «a в степени n».
Степенное выражение представляет собой такое выражение, в состав которого входит степень.
Перед тем, как рассмотреть действия со степенными выражениями, полезно вспомнить свойства степени:
Правила умножения, что происходит
Если степени имеют одинаковые показатели, то в процессе их перемножения следует умножить между собой основания, а показатель записать без изменений:
где а и b являются основаниями степени, n — это показатель степени в виде какого-либо натурального числа.
В качестве примера решим несколько простых уравнений:
a 5 × b 5 = ( a × a × a × a × a ) × ( b × b × b × b × b ) = ( a × b ) n = ( a b ) × ( a b ) × ( a b ) × ( a b ) × ( a b ) = ( a b ) 5
3 5 × 4 5 = ( 3 × 4 ) 5 = 12 5 = 248832
16 a 2 = 4 2 × a 2 = ( 4 a ) 2
Когда требуется найти произведение степеней, которые обладают одинаковыми основаниями, следует сложить показатели степеней:
В качестве примеров рассмотрим несколько вычислений:
3 5 × 3 2 = 3 5 + 3 = 3 8 = 6561
2 8 × 8 1 = 2 8 · 2 3 = 2 11 = 2048
При умножении чисел, которые имеют разные степени, но схожи по основаниям, необходимо руководствоваться правилом, рассмотренным в предыдущем примере. То есть:
где а и b являются основаниями степени, n — это показатель степени в виде какого-либо натурального числа.
Бывают ситуации, когда числа отличаются по степеням и по основаниям, а также какое-то из оснований невозможно преобразовать в число с аналогичной степенью, как у второго числа. В этом случае нужно возвести в степень каждое число, а на втором шаге выполнить умножение.
3 3 × 5 2 = 27 × 25 = 675
Правила деления
Когда требуется выполнить деление степеней, которые имеют разные основания, но схожи по показателям, нужно найти разность показателей и оставить основание без изменений:
где а является основанием степени, n и m — это показатели степени в виде каких-либо натуральных чисел, m>n.
В качестве примеров рассмотрим несколько выражений:
Деление степеней, которые имеют одинаковые показатели, подразумевает возведение результата частного данных чисел в степень:
где а и b являются основаниями степени в виде любых рациональных чисел, не равных нулю, n — это показатель степени в виде какого-либо натурального числа.
5 12 ÷ 3 12 = ( 5 ÷ 3 ) 12 = ( 1 2 3 ) 12
Предположим, что требуется выполнить деление чисел со степенями. При этом степени не одинаковые, а основания идентичные. Тогда следует руководствоваться правилом, рассмотренным в предыдущем примере:
В том случае, когда отличаются не только степени, но и основания, необходимо возвести в степень каждое из чисел, а затем выполнить умножение. Например:
Примеры решения заданий для 7 класса
Воспользуемся правилом умножения степеней, имеющих одинаковое основание:
Воспользуемся правилом умножения степеней, имеющих одинаковое основание, чтобы избавиться от необходимости возводить число в большую степень:
2 7 = 2 3 × 2 4 = 8 × 16 = 128
Воспользуемся правилом умножения степеней, имеющих разные основания, но одинаковые показатели:
3 2 × 2 2 = ( 3 × 2 ) 2 = 6 2 = 36
Здесь можно применить правило деления степеней с одинаковым основанием и разными показателями:
Здесь можно применить правило деления степеней с одинаковым основанием и разными показателями:
Воспользуемся свойством деления степеней, когда основания отличаются, а показатели совпадают:
Отрицательная степень
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Свойства степеней
Степень с натуральным показателем в математике имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
Свойство 4: степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень сначала делимое, потом делитель, и первый результат разделить на второй.
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0; 0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Как делить степени
Как делить степени? При каких условиях деление степеней возможно?
В алгебре найти частное степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
Чтобы разделить степени с одинаковыми основаниями, надо основание оставить прежним, а из показателя степени делимого вычесть показатель степени делителя (или коротко: при делении степеней показатели вычитают):
(последнюю формулу удобно использовать, если показатель степени в знаменателе больше показателя степени в числителе).
При делении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как делить степени, на конкретных примерах.
Единицу в показателе степени не пишут, но при делении степеней ее следует учесть:
При делении степеней с одинаковыми основаниями и одинаковыми показателями получаем единицу:
Вынесение общего показателя при делении степеней позволяет упростить вычисления:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число разделить на степень либо степень разделить на число, сначала следует выполнить возведение в степень, а затем — деление: