Рабочий обслуживает 5 одинаковых станков вероятность того что в течение часа

Решение задач о станках. Почти полное руководство

В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков.

В этот раз рассмотрим задачи о станках, и остановимся на трех типах задач: на действия с событиями (станки выходят из строя с разными вероятностями), на формулу Бернулли (вероятности одинаковы) и на формулу полной вероятности и Байеса.

Если вы только учитесь решать задачи, рекомендуем читать всю статью целиком, чтобы понять принцип решения и формулы в каждом случае, научиться отличать задачи друг от друга и подбирать верный подход. Знаете что конкретно ищете? Переходите по ссылкам.

Капризные станки и вероятности

Рассмотрим популярный класс задач: про рабочего и капризные станки, которые ломаются/требуют внимания рабочего, причем вероятности выхода из строя заданы и различны для каждого из станков. Нужно найти вероятность выхода из строя одного станка, двух, ни одного и так далее, в зависимости от конкретной задачи.

Теория: выписываем события

Рассматривать в примере будем случаи с 2 или 3 станками. С одним задача вырождается, с четырьмя становится довольно громоздкой, но решается аналогично рассмотренным ниже.

Теория: случай 2 станков

Теория: случай 3 станков

Ни один станок не отказал:

Все три станка отказали:

Практика: укрощаем станки

Пример 1. Два станка работают независимо друг от друга. Вероятность того, что первый станок проработает смену без наладки, равна 0,9, а второй – 0,8. Найти вероятность того, что: а) оба станка проработают смену без наладки, б) оба станка за смену потребуют наладки.

Итак, случай с 2 станками, используем формулы (1) и (3), чтобы найти искомые вероятности. Важно, какое событие мы считаем базовым: выше в теории мы использовали «станок откажет», тут же удобнее событие «станок проработает смену» (при этом формулы сохраняют вид, но легко использовать не ту, будьте внимательны).

1) Оба станка проработают смену без наладки:

2) Оба станка за смену потребуют наладки:

Пример 2. Вероятности бесперебойной работы для каждого из двух станков соответственно равны 0,95 и 0,8. Найти вероятность того, что за смену: а) произойдет остановка только одного станка; б) остановится хотя бы один станок.

Еще одна задачка про 2 станка. Так как в вопросах идет речь именно об остановках станка, их и будем считать базовыми событиями:

а) произойдет остановка только одного станка (используем формулу (2)):

б) В этом случае удобно сначала найти вероятность противоположного события «Ни один станок не остановится» (оба работают):

Тогда вероятность того, что остановится хотя бы один станок, равна:

Теперь рассмотрим пример задачи с тремя станками, в которой используем все формулы, выведенные выше (см. (4)-(7)).

Также эту вероятность можно выразить через уже найденные ранее:

Пример 4. Рабочий обслуживает три станка. Вероятность выхода из строя за смену для них, соответственно, равна 0,75; 0,8 и 0,7. Найти вероятность того, что за смену выйдут из строя не менее двух станков.

Тогда искомая вероятность:

И, наконец, рассмотрим одну задачу с четырьмя станками.

Пример 5. Рабочий обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что в течение смены первый станок потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвёртый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок потребует внимания мастера.

Вероятность нужного события тогда:

Одинаковые станки и формула Бернулли

Пример 6. Рабочий обслуживает пять однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение дня, равна 0,3. Найти вероятность того, что в течение дня этих требований будет ровно четыре.

Найдем вероятность того, что ровно 4 станка потребуют внимания рабочего по формуле (8):

Пример 7. Вероятность поломки одного из 6 работающих независимо друг от друга станков равна 0,2. Если происходит поломка, станок до конца дня не работает. Какова вероятность того, что в течение дня сломается более 2 станков?

Найдем вероятность того, что в течение дня сломается более двух станков, используя переход к противоположному событию (в течение дня сломается 0, 1 или 2 станка):

Пример 8. На рабочем участке 5 однотипных станков. Вероятность того, что каждый из них исправен, равна 0,8. Плановое задание может быть выполнено, если исправно не менее 3 станков. Какова вероятность, что задание будет выполнено?

Думаю, тут можно обойтись только формулой, согласны?

Пример 9. В цехе работают 8 станков. Вероятность безотказной работы каждого 0,9. Найти вероятность того, что хотя бы один станок откажет в работе.

Как и почти всегда, когда в задаче есть «хотя бы один», используем переход к противоположному событию «Все станки работают»:

Задачи на полную вероятность

Рассмотрим еще один тип задач со станками, который оооочень распространен в домашних и контрольных работах, и относится к теме полной вероятности.

Теорию вы сможете найти по ссылке выше, а тут я кратко напомню основные шаги:

Пример 10. В цехе работают 20 станков. Из них 10 марки А, 6 марки В и 4 марки С. Вероятность того, что качество детали окажется отличным для этих станков соответственно равна 0,9; 0,8; 0,7. Какой процент отличных деталей выпускает цех в целом?

Введем полную группу гипотез:
$Н_1$ = (Деталь изготовлена на станке марки А),
$Н_2$ = (Деталь изготовлена на станке марки В),
$Н_3$ = (Деталь изготовлена на станке марки С).

Вероятности гипотез найдем как отношение числа станков нужной марки к общему числу станков в цехе:

Получили 0,83 или 83% отличных деталей в цехе.

Пример 11. Три станка подают детали в общий бункер. Вероятность выпуска бракованной продукции для первого станка 0,03, для второго – 0,02, и для третьего 0,01. Производительность первого станка в 3 раза больше производительности второго, а производительность третьего в два раза больше второго. Какова вероятность того, что взятая наудачу деталь из бункера окажется годной?

Вероятность того, что взятая наудачу деталь из бункера окажется годной, находим по формуле полной вероятности (9):

Пример 12. На склад поступили детали с 3-х станков. На первом станке изготовлено 40% деталей от их общего количества, на 2-ом – 35% и на третьем – 25%. Причем на первом станке было изготовлено 90% деталей 1-го сорта, на втором 80% и на третьем – 70%. Известно, что наугад выбранная со склада деталь оказалась деталью 1-го сорта. Найти вероятность того, что она была изготовлена на 2-м станке.

Найдем апостериорную вероятность того, что деталь изготовлена на втором станке, если она оказалась 1-го сорта, используя формулу Байеса (10):

Полезные ссылки по ТВ

Решебник по вероятности

А здесь вы найдете почти 300 задач о станках с полными решениями (вводите часть текста для поиска своей задачи):

Источник

Теория вероятностей

Министерство образования и науки Российской Федерации

Бузулукский гуманитарно-технологический институт (филиал) государственного образовательного учреждения высшего профессионального образования

«Оренбургский государственный университет»

Факультет заочного обучения

Кафедра физики, информатики, математики

по дисциплине Математика

Студент з-09 ПГС группы

Какова вероятность того, что в течение часа:

а) ни один станок не потребует внимания рабочего;

б) все три станка потребуют внимания рабочего;

в) какой-нибудь один станок потребует внимания рабочего;

г) хотя бы один станок потребует внимания рабочего?

а) А (i =1,2,3) – не потребует внимания станок в течение часа

В – событие, где все 3 станка не потребуют внимания рабочего в течение часа

Р (В) = Р (А1 × А2 × А3) = Р(А1) × Р(А2) × Р(А3) = 0,9 × 0,8 × 0,85 = 0,612

б) А (i =1,2,3) – не потребует i-й внимания станок

Ᾱ (i =1,2,3) – потребует i-й внимания станок, независимое событие

Р (Ᾱ 3) = 1 – 0,85 = 0,15

Р (Ᾱ 1 × Ᾱ 2 × Ᾱ 3) = (0,1 × 0,2 × 0,15) = 0,003

в) Ᾱ 1 = 0,1; Ᾱ 2 = 0,2; Ᾱ 3 = 0,85

Аi – один станок потребует внимания рабочего в течение часа

Р (В) = Р (А1 × Ᾱ 2 × А3 + Ᾱ 1 × А2 × А3 + А1 × А2 × Ᾱ 3) = (0,9× 0,2 × 0,85 + 0,1 × 0,8 × 0,85 + 0,9 × 0,8 × 0,15) = 0,329

г) Найдём вероятность через противоположное событие, т.е. ни один станок не потребует внимания рабочего в течение часа

Р (А1 × А2 × А3) = Р (А1) × Р (А2) × Р (А3) = 0,9 × 0,8 × 0,85 = 0,612

Р ( С) = 1 – 0,612 = 0,388

Ответ: а) вероятность равна 0,612, что в течение часа ни один станок не потребует внимания рабочего; б) вероятность равна 0,003, что в течение часа все три станка потребуют внимания рабочего; в) вероятность равна 0,329, что в течение часа какой-нибудь один станок потребует внимания рабочего; г) вероятность равна 0,388, что в течение часа хотя бы один станок потребует внимания рабочего.

Ящик содержит 10 деталей, среди которых 3 стандартные. Найти вероятность того, что среди отобранных 5 деталей окажутся: а) только 2 стандартные детали; б) все детали нестандартные; в) все детали стандартные; г) хотя бы одна деталь стандартная.

а) число способов, где взяли 5 деталей из 10 детали, можно подсчитать по формуле:

С2 – число способов, где взяли 2 стандартные детали из 3-х нестандартных

С3 – число способов, где взяли 3 стандартные детали из 7-ми нестандартных

С5 – всего способов, где взяли 5 стандартных деталей из 10-ти

С2 =__3!___ = 3 С3 = __7!___ = 35 С5 = __10!___ = 252

С3 × С7 = 3 × 35 = 0,417

б) С7 – число способов выбора, где взяли 5 деталей из 7-ми

Число выбора деталей считается в сочетании С5 = 1

С7 – число способов, где взяли 5 деталей из 7-ми

С10 – всего способов, где взяли 5 деталей из 10-ти

Искомая вероятность Р ( Д):

Р (Д) = С7 × С3 = 21 × 1 = 0,083

в) Событие, где взяли 5 стандартных деталей из 3-х стандартных деталей невозможно. Вероятность равна нулю.

г) Найдём искомую вероятность через противоположное событие:

С7 – число способов, где взяли 5 нестандартных деталей из 7-ми

С3 – число способов выбора из 3-х

С10 – всего способов, где взяли 5 деталей из 10-ти

Ответ: а) Если среди отобранных 5 деталей окажутся только 2 стандартные детали, то вероятность равна 0,417; б) если среди отобранных 5 деталей окажутся все детали нестандартные, то вероятность равна 0,083; в) если среди отобранных 5 деталей окажутся все детали стандартные, то вероятность равна 0; г) если среди отобранных 5 деталей окажется, хотя бы одна деталь стандартная, то вероятность равна 0,083.

Решение: I ящик II ящик

Доброкачественные 50 × 50 изделия Н1 – взяли из I ящика с доброкачественными изделиями, то Р ( Н1) = 0,5

Н2 – взяли из II ящика, то Р ( Н2) = 0,5

Событие А, где взяли доброкачественную деталь, Р ( А ǀ Н1) = 1

Событие А ǀ Н1 – доброкачественная деталь из I ящика

Событие А ǀ Н2 – из II ящика, Р ( А ǀ Н2) = 0,5

Тогда искомая вероятность Р ( А ) =Р ( Н1 ) × Р ( А ǀ Н1 ) + Р ( Н2 ) × Р (А ǀ Н2)

Р ( А) = 0,5 × 1 + 0,5 × 0,5 = 0,5 + 0,25 = 0,75

Р ( Н1 ) × Р ( А ǀ Н1 ) ˃ Р ( Н2 ) × Р ( А ǀ Н2)

Ответ: Если изделие принадлежит первому и второму ящику, и количество изделий в ящиках одинаково, то вероятности отличаются на 0,75.

Р ( А ǀ Н1 ) = 0,7 Р ( А ǀ Н2 ) = 0,85 Р ( А ǀ Н3 ) = 0,9

Р ( А) = 0,7 × 0,85 × 0,9 = 0,536

А – взятое изделие отличного качества из II станка

Искомая вероятность равна:

Р ( Н2 ǀ А ) = ________ Р ( Н2 ) × Р ( А ǀ Н2)

Р ( Н1 ) × Р ( А ǀ Н1 ) + Р ( Н2 ) × Р ( А ǀ Н2 ) + Р ( А ǀ Н3)

Где Н1, Н2, Н3 – соответственно изготовлено изделий на станках I, II и III.

Р ( А ǀ Н1) = 0,7 – вероятность отличной детали I станка

Р ( А ǀ Н2) = 0,85 – вероятность отличной детали II станка

Р ( А ǀ Н3) = 0,9 – вероятность отличной детали III станка

Р ( Н2 ǀ А) = ________ 0,346 × 0,85 ______________ = 0,294 = 0,365

0,385 × 0,7 + 0,346 × 0,85 + 0,269 × 0,9 0,806

Ответ: Вероятность равна 0,365, что взятое наудачу изделие оказалось отличного качества изготовлено на втором станке.

Найти вероятность того, что событие А произойдет не менее 2 раз в 4 независимых испытаниях, если вероятность наступления события А в одном испытании равна 0,6.

Событие А произойдёт не менее 2-х раз в 4 независимых испытаниях

q = 1 – р = 1 – 0,6 = 0,4

– вероятность противоположного события. Нет наступления события А в 1-ом испытании.

Найдём произведение npq и определим формулу вычисления:

вероятность случайный величина интегральный

n = 4 npq = 4 × 0,6 × 0,4 = 0,96

Можно использовать формулу Бернули:

Р ( А) = С2 × p2 × q2 + С3 × р3 × q1 + С4 × р4 × q0

Найдём через противоположное событие:

Р ( А) = 1 – С0 × p0 × q4 + С1 × p1 × q3 = 1 – 1 × 1 × (0,4)4 + 4 × 0,6 × (0,4)3 = 1 – 0,0256 + 4 × 0,6 × 0,064 = 0,9744 + 0,1536 = 1,128

Ответ: Если событие А произойдет не менее 2 раз в 4 независимых испытаниях, то вероятность равна 1,128.

Вероятность того, что пара обуви, наудачу из изготовленной партии, окажется 1-го сорта, равна 0,7. Определить вероятность того, что из 2100 пар, поступающих на контроль, число пар первосортной обуви окажется не менее 1000 и не более 1500.

Для решения задачи используем интегральную формулу Муавра – Лапласа.

Вероятность событий Рn (m1 ˂ m ˂ m2) = Ф (х2) – Ф (х1)

р = 0,7; n = 2100; m1 = 1000; m2 = 1500; q = 0,3

х1 = _m1 – np_ = 1000 – 2100 × 0,7 = 1000 – 1470 = – 470 = – 22,38

√ npq √2100 × 0,7 × 0,3 √441 21

х2 = _m2 – np_ = 1500 – 2100 × 0,7 = 1500 – 1470 = _30_ = 1,43

√ npq √2100 × 0,7 × 0,3 √441 21

Ф ( – х) = – Ф (х) Ф (– 22,38) = 0,5 Ф (– 22,38) = 0,4236

Ф (х2) – Ф (х1) = Ф (х2) + Ф (х1) = 0,5 + 0,4236 = 0,9236

Ответ: Если число пар первосортной обуви окажется не менее 1000 и не более 1500, то из 2100 пар, поступающих на контроль, равна вероятности 0,9236.

Случайная величина Х задана интегральной функцией F(x). Требуется: а) найти дифференциальную функцию f(х) (плотность вероятности), б) найти математическое ожидание и дисперсию Х, в) построить графики интегральной и дифференциальной функций, г) вероятность попадания случайной величины Х в интервал .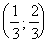

По определению Fʹ (х) = f (х)

Fʹ ( х ) = 0ʹ = 0 Fʹ ( х ) = ( х2 ÷ 4 )ʹ = 0,5х Fʹ ( х ) = 1ʹ = 0

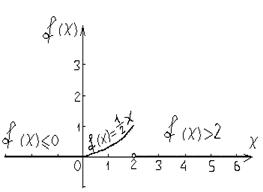
в) Построение графиков интегральной и дифференциальной функции.

б) М (Х) = х f (х) dx = 0 dx + х × _1_ dx + 0 dx =_ 1_ × х3 ÷ 3 = х3 ÷ 6 =

2 2 =_ 23_ – _03 = 8 – 0 = 4 = а

Д (Х) = (х – _4_)2 f (х) dx = 0 (х – _4)2 f (х) dx + (х – 4)2 1 х dx +

= 1_ × 24 – 4 × 23 + 8_ × 22 = 16 – 32 + 16 = 144 – 128 = 16 = _2_

2 4 3 3 9 2 8 9 9 72 72 9

г) Р ( 1 ˂ Х ˂ 2) = F (в) – F (а) 22 × 1 – 12 × 1 = _1 – _1 = _1_ ––

вероятность попадания в этот промежуток.

Ответ: М (Х) = _4 = а ; Д (Х) = _2 ; Р ( 1 ˂ Х ˂ 2) =_ 1_

Найти вероятность попадания в заданный интервал ( a,b ) нормально распределенной случайной величины Х, если известны ее математическое ожидание а и среднее квадратическое отклонение s.

a = 2, b = 13, а = 10, s = 4.

Если случайная величина Х нормально распределена, то она является непрерывной случайной величиной, и М (Х) вычисляется, как: (a + b) ÷ 2, а Д (Х) вычисляется, как: (b-a) ÷ (в-а), и s связаны формулой √ Д.

Тогда вероятность: Р < Х ϵ [a,b] >будет вычисляться по формуле:

Ф ( ( b – a ) ÷ s) – Ф ( (a – b) ÷ s ).

М (Х) = (a + b) ÷ 2 = (2 + 13) ÷ 2 = 7,5

s = √ Д = √ 0,75 = 0,87 × 100 = 87

То искомая вероятность находится по формуле:

Р (a ˂ Х ˂ b ) = Ф ( ( b – a ) ÷ s ) – Ф ( (a – b) ÷ s ) = Ф ((13 – 10) ÷ 4) –

Ф ((2 – 10) ÷ 4) = Ф (0,75) – Ф (– 2) = Ф (0,75) + Ф (2) = 0,2734 + 0,5 =

Где Фх – функция Лапласа, которую находим по таблице.

Ответ: Вероятность попадания в заданный интервал ( a,b ) нормально распределенной случайной величины Х, равна 0,773.

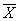
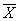
Найти доверительные интервалы для оценки математического ожидания нормального распределения с надежностью 0,95, если выборочная средняя , объем выборки n и среднее квадратическое отклонение s.

= 12, 15, n = 169 s = 5

Находим доверительные интервалы: х – t γ ˂ а ˂ х + t γ

где Ф (t) = Ф (γ ÷ s) → t = (γ ÷ s) = (0,95 ÷ 5) = 0,19

х – t γ = 12,15 – 0,19 × 0,95 = 12,15 – 0,01 = 12,14

х + t γ = 12,15 + 0,19 × 0,95 = 12,15 + 0,01 = 12,16

Ответ: Доверительные интервалы 12,14 ˂ а ˂ 12,16.

1. Севастьянов Б.А., Чистяков В.П, Зубков А.М. Сборник задач по теории вероятностей – М.: Наука, 1980.

2. Шипачев В.С. Высшая математика. М.: Высшая школа, 2004.

3. Чистяков В.П. Курс теории вероятности, М.: 2001.

4. Гмурман В.Е. Теория вероятностей и математическая статистика.- М.: Высшая школа, 2003.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.- М.: Высшая школа, 2003.

6. Данко П.Е и др. Высшая математика в упражнениях и задачах (I и II часть).-М, 2005.

7. Богаров П.П., Печинкин А.В. Теория вероятностей. Математическая статистика – М.: 1998.

8. Венцель Е.С. Теория вероятностей – М.: 1962.

9. Солодовников А.С. Теория вероятностей М.: Просвещение, 1978.

10. Виленкин Н.Я., Потапов В.Т. Задачник-практикум по теории вероятности с элементами комбинаторики и математической статистики.

11. Кремер Н.Ш.: «Теория вероятностей и математическая статистика»; М.ЮНИТИ – Дана, 2003.

Источник

LiveInternetLiveInternet

—Ссылки

—Рубрики

—Метки

—Приложения

—Поиск по дневнику

—Подписка по e-mail

—Статистика

100 готовых задач по теории вероятностей часть 18

1701. Вероятность появления события A в отдельном испытании равна 0,75. Какова вероятность того, что при восьмикратном повторении испытания это событие появится более 6 раз? Готовое решение задачи

1702. Вероятность появления события А при одном испытании равна 0,1. Найти вероятность того, что при 3 независимых испытаниях оно появится хотя бы один раз. Готовое решение задачи

1703. Вероятность появления события А при одном испытании равна 0,1. Найти вероятность того, что при трех независимых испытаниях оно появится: а) не менее двух раз; б) хотя бы один раз. Готовое решение задачи

1704. Вероятность появления события А при одном испытании равна 0,1. Найти вероятность того, что при трех независимых испытаниях оно появится а) ровно 2 раза, б) не менее 2 раз. Готовое решение задачи

1705. Вероятность попадания в цель при одном выстреле – 0,6. Найти: а) вероятность того, что при 5400 выстрелах цель будет поражена 3240 раз, б) наиболее вероятное число попаданий при 5400 выстрелах. Готовое решение задачи

1706. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность трех попаданий при четырех выстрелах. Готовое решение задачи

1707. Производится 6 выстрелов по цели. Вероятность попадания в цель при каждом выстреле равна 0,4. Найти вероятность того, что: а) произойдет одно попадание в цель; б) произойдет не менее 4 попаданий; в) произойдет хотя бы одно попадание. Готовое решение задачи

1708. Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 8 выстрелов дадут 5 попаданий? Готовое решение задачи

1709. Из одной ЭВМ в другую необходимо переслать файл объемом 10000 символов. Вероятность ошибки при передаче составляет 0,001. Вычислить вероятность того, что в переданном файле будет ровно 10 ошибок. Готовое решение задачи

1710. Рабочий обслуживает 50 станков. Вероятность того, что в течение смены станок потребует регулировки, равна 1/3. Что более вероятно: а) Регулировки требуют 17 станков. б) Регулировки требуют 16 станков. Готовое решение задачи

1711. Рабочий обслуживает 5 одинаковых станков. Вероятность того, что в течение часа станок потребует регулировки, равна 1/3. Какова вероятность того, что в течение часа рабочему придется регулировать 4 станка? Готовое решение задачи

1712. Рабочий обслуживает 4 однотипных станка. Вероятность того, что в течение часа станок потребует регулировки, равна 1/3. Какова вероятность того, что в течение часа рабочему придётся регулировать не более одного станка? Готовое решение задачи

1713. Рабочий обслуживает 5 станков. Вероятность остановки станка в течение рабочего дня равна 0,2. Какова вероятность того, что в течение рабочего дня не произойдет остановки хотя бы одного станка? Готовое решение задачи

1714. Рабочий обслуживает 4 однотипных станка. Вероятность того, что в течение часа станок потребует регулировки, равна 1/3. Какова вероятность того, что в течение часа рабочему придётся регулировать ровно 2 станка? Готовое решение задачи

1715. Рабочий обслуживает 12 станков одного типа. Вероятность того, что станок потребует внимание рабочего в течение часа, равна 1/3. Найти: а) вероятность того, что в течение часа 4 станка потребуют внимания рабочего; б) наиболее вероятное число станков, которые потребуют внимания рабочего в течение часа. Готовое решение задачи

1716. Рабочий обслуживает 12 станков одного типа. Вероятность того, что станок требует внимания рабочего в течение часа, равна 1/4. Найдите вероятность того, что в течение часа 2 станка потребуют внимания рабочего. Готовое решение задачи

1717. Рабочий обслуживает 10 однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение часа, равна 0,05. Найти вероятность того, что в течение часа потребует внимания не более двух станков. Готовое решение задачи

1718. Рабочий обслуживает десять однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение часа, равна 0,05. Найти вероятность того, что в течение часа этих требований будет от трех до пяти. Готовое решение задачи

1719. Рабочий обслуживает десять однотипных станков. Вероятность того, что станок потребует внимания рабочего, одинакова для каждого из десяти станков и равна 0,05. Найти вероятность того, что в течение часа этих требований будет не меньше одного, но и не больше трех (пренебречь вероятностью того, что один станок может потребовать внимания рабочего в течение часа более одного раза). Готовое решение задачи

1720. Рабочий обслуживает 10 однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение часа, равна 0,05. Найти вероятность того, что:
а) в течение часа этих требований будет ровно 4;
б) в течение часа будет не меньше двух таких требований. Готовое решение задачи

1721. В течение года град приносит значительный ущерб одному хозяйству из m=3. Определить вероятность того, что из n=100 хозяйств, имеющихся в области, пострадает не менее восьми хозяйств. Готовое решение задачи

1722. Вероятность, что покупатель сделает покупки 0,4. Найти вероятности: а) из 5 покупателей 2 сделает покупки, б) из 30 покупателей 20 сделает покупки, в) из 60 покупателей меньше 20 сделает покупки. Готовое решение задачи

1723. Аудитор проверяет n=9 документов на наличие ошибок. Вероятность нахождения ошибки дела для каждого дела одна и та же и равна p=0,8. Какова вероятность того, что из 9 дел ошибка будет обнаружена не менее чем в трех? Готовое решение задачи

1724. В областной олимпиаде по математике принимает участие n=100 студентов. Вероятность того, что каждый претендент ответит на все вопросы олимпиады, равна p=0,05. Какова вероятность того, что ровно 3 студента пройдут данный этап олимпиады, ответив на все вопросы? Готовое решение задачи

1725. Аудитор проверяет n=7 документов на наличие ошибок. Вероятность нахождения ошибки дела для каждого дела одна и та же и равна p=0,6. Какова вероятность того, что из 7 дел ошибка будет обнаружена не менее чем в трех? Готовое решение задачи

1726. В областной олимпиаде по математике принимает участие n=105 студентов. Вероятность того, что каждый претендент ответит на все вопросы олимпиады, равна p=0,01. Какова вероятность того, что ровно 3 студента пройдут данный этап олимпиады, ответив на все вопросы? Готовое решение задачи

1727. Аудитор проверяет n=8 документов на наличие ошибок. Вероятность нахождения ошибки дела для каждого дела одна и та же и равна p=0,4. Какова вероятность того, что из 8 дел ошибка будет обнаружена не менее чем в трех? Готовое решение задачи

1728. В областной олимпиаде по математике принимает участие n=120 студентов. Вероятность того, что каждый претендент ответит на все вопросы олимпиады, равна p=0,02. Какова вероятность того, что ровно 3 студента пройдут данный этап олимпиады, ответив на все вопросы? Готовое решение задачи

1729. Всхожесть семян ржи составляет 80%. Чему равна вероятность, что из 10 посевных семян взойдет 4? Готовое решение задачи

1730. Известно, что 3/5 количества обуви, изготовленной фабрикой, оценивается как продукция 1-го сорта. Нужно определить вероятность того, что среди 200 пар изготовленной обуви будет 140 пар 1-го сорта. Готовое решение задачи

1731. Известно, что 3/5 обуви, изготовленной фабрикой, оценивается как продукция 1 сорта. Какова вероятность того, что среди наугад взятых 400 пар обуви, изготовленной фабрикой, 1 сорта будет:
1) 250 пар;
2) от 250 до 300 пар Готовое решение задачи

1732. Опытным путем установлено, что доля волокна хлопка-сырца длиной а составляет в среднем 10 % в каждой подопытной партии. Какова вероятность появления волокна указанной длины 150 раз при 1700 опытах? Готовое решение задачи

1733. Опытным путем установлено, что доля волокна хлопка-сырца длиной а составляет в среднем 10 % в каждой подопытной партии. Какова вероятность появления в 1600 опытах: а) от 130 до 190 коротких волокон; б) ровно 160 коротких волокон Готовое решение задачи

1734. Каждый моряк из экипажа прибывшего в порт судна с вероятностью, равной 1/3, осматривает город, остается на корабле или находится в ресторане. Найти вероятность того, что из 203 членов экипажа в данный момент 71 моряк осматривает город. Готовое решение задачи

1735. Батарея сделала 14 выстрелов по объекту, вероятность попадания в который равна 0,2. Найти: а) наивероятнейшее число попаданий и его вероятность; б) вероятность разрушения объекта, если для этого необходимо не менее 4 попаданий. Готовое решение задачи

1736. Батарея дала 140 выстрелов по военному объекту, вероятность попадания в который равна 0,2. Найдите наивероятнейшее число попаданий и его вероятность. Готовое решение задачи

1737. Вероятность попадания при каждом выстреле равна 0,4. Найти вероятность разрушения объекта, если для этого необходимо не менее 3 попаданий, а сделано 15 выстрелов. Готовое решение задачи

1738. На факультете учатся 500 студентов. Найдите вероятность того, что первое сентября является днём рождения не более одного студента? Готовое решение задачи

1739. Вероятность появления события А в каждом из независимых испытаний равна р = 0,9. Произведено n = 150 испытаний. Найти вероятность того, что в этих испытаниях событие А появится: 1) не более k = 130 раз, 2) не менее k = 130 раз. Готовое решение задачи

1740. Определите наивероятнейшее число попаданий m₀, если вероятность попадания в цель при одном выстреле равна 0,6. Серия состоит из 8 выстрелов. Готовое решение задачи

1741. Вероятность попадания стрелком в цель равна 0,6. Сделано 30 выстрелов. Определить наивероятнейшее число попаданий в цель. Готовое решение задачи

1742. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель. Готовое решение задачи

1743. Доля брака при производстве некоторой продукции составляет 1,8 %. Определить наивероятнейшее число бракованных единиц в партии из 600 штук продукции, а также найти вероятность этого числа. Готовое решение задачи

1744. Доля брака в некоторой продукции составляет 3%. В партии 800 изделий. Какова вероятность наиболее вероятного числа бракованных изделий в этой партии? Готовое решение задачи

1745. Бракованные изделия, выпускаемые некоторым заводом, составляют в среднем 1,5%. Какое наивероятнейшее количество бракованных изделий будет в партии из 220 штук? Сколько нужно закупить изделий, чтобы наивероятнейшее число годных было равно 250? Готовое решение задачи

1746. Стрелок стреляет по мишени 10 раз. Вероятность попадания при одном выстреле р = 0,8. Вероятность того, что будет точно 8 попаданий равна. Готовое решение задачи

1747. Стрелок стреляет по мишени 10 раз. Вероятность попадания при одном выстреле р = 0,75. Вероятность того, что будет не менее 9 попаданий равна Готовое решение задачи

1748. Что вероятнее выиграть 1 партию из 3, или 2 из 5,с равными соперниками и ничья невозможна? Готовое решение задачи

1749. Местная милиция сформировала статистические данные по трезвости водителей за рулем путем остановки автомобилей наугад. Вероятность обнаружения нетрезвого водителя составила 0,2. Какая вероятность, что среди 9-ти проверенных водителей, не более двух находились в состоянии опьянения? Ровно три водителя? Готовое решение задачи

1750. Рабочий обслуживает три узла технологической линии. Вероятность того, что в течение смены внимания рабочего потребует первый узел, равная 0,7, второй – 0,75, третий – 0,84. Найти вероятность того, что в течение смены внимания рабочего потребуют любые два узла. Готовое решение задачи

1751. Рабочий обслуживает три станка. Вероятность того, что в течение смены его внимания потребует первый станок, равна 0,7, второй – 0,75, третий – 0,8. Найти вероятность того, что в течение смены внимания рабочего потребуют не менее двух станков. Готовое решение задачи

1752. Рабочий обслуживает три станка. Вероятность того, что в течение смены потребует внимания первый станок, равна 0,7, второй 0,75, третий 0,8. Найти вероятность того, что в течение смены: а) потребует внимания рабочего какие-либо два станка. б) ни один станок не потребует внимания рабочего. Готовое решение задачи

1753. Количество качественных деталей в партии составляет 70%. Найти вероятность того, что из взятых наудачу 10 деталей 8 окажутся качественными. Готовое решение задачи

1754. При данном технологическом процессе 79 % всей производственной продукции оказывается продукцией высшего сорта. Найти наивероятнейшее число изделий высшего сорта в партии из 150 изделий. Вычислить вероятность того, что в этой партии окажется наивероятнейшее число изделий высшего сорта. Готовое решение задачи

1755. Вероятность попадания по движущейся мишени – 0,7. Какова вероятность того, что из 20 выстрелов 15 окажутся удачными? Готовое решение задачи

1756. Вероятность попадания при каждом выстреле по движущейся мишени равна 0,6. Какова вероятность того, что из 25 выстрелов 10 окажутся точными? Готовое решение задачи

1757. Вероятность попадания по мишени при каждом выстреле 0,6. Найти вероятность того, что при 30 выстрелах число попаданий будет от 15 до 20. Готовое решение задачи

1758. Вероятность того, что ПК потребует обновления в течение одного года, равна 0,2. Найти вероятность, что в партии, содержащей 150 ПК, обновления в течение года потребуют ровно 20. Готовое решение задачи

1759. Доля бракованных изделий, выпускаемых заводом, равна 2%. Найти вероятность появления 30 бракованных изделий в партии, содержащей 200 изделий. Готовое решение задачи

1760. Вероятность появления брака в партии из 500 изделий равна 0,035. Найти наивероятнейшее число бракованных изделий в партии и его вероятность. Готовое решение задачи

1761. На факультете 500 студентов. Найти наиболее вероятное число студентов, родившихся 1 сентября, и вероятность этого числа рождений. Вероятность рождения 1 сентября принять равной 0,0027. Готовое решение задачи

1762. Вероятность изготовления годной детали на станке равна 0,9. Сколько нужно обработать деталей, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 деталей будут годными? Готовое решение задачи

1763. Вероятность успешной сдачи экзамена каждым студентом заочного факультета равна 0,9. У скольких студентов надо принять экзамен, чтобы с вероятностью 0,98 можно было ожидать, что не менее 120 студентов сдадут экзамен. Готовое решение задачи

1764. Даша решила участвовать в двух лотереях, которые не зависят одна от другой. Она купила по одному билету из каждой лотереи. Вероятность выиграть в первой лотерее равняется 0,5, а во второй 0,4. Какая вероятность, что Даша выиграет в обеих лотереях? Готовое решение задачи

1765. Адвокат ведет в суде дела десяти клиентов. Вероятность выигрыша дела для каждого клиента одна и та же и равна 0,4. Какова вероятность того, что из десяти дел будут выиграны не более трех? Готовое решение задачи

1766. Адвокат ведет в суде дела десяти клиентов. Вероятность выигрыша дела для каждого клиента одна и та же и равна 0,4. Какова вероятность того, что из десяти дел будет выиграно три? Готовое решение задачи

1767. Предприятие выпускает 40% изделий высшего сорта. Какова вероятность того, что среди наудачу взятых 400 изделий – высшего сорта будет не менее 200? Готовое решение задачи

1768. Вероятность изготовления стандартной детали равна 0,8. Найти наивероятнейшее число стандартных деталей среди 8 отобранных и его вероятность. Готовое решение задачи

1769. Вероятность выиграть по одному билету лотереи 1/7. Какова вероятность выиграть: а) 4 билета из 5; б) хотя бы по одному билету. Готовое решение задачи

1770. Вероятность выиграть по одному билету лотереи равна 1/6. Какова вероятность, имея 5 билетов лотереи выиграть хотя бы по одному билету; по 3 билетам? Готовое решение задачи

1771. Вероятность выигрыша по одному билету лотереи равна 1/7. Какова вероятность того, что лицо, имеющее шесть билетов:
а) выиграет по двум билетам;
б) выиграет по трем билетам;
в) не выиграет по двум билетам? Готовое решение задачи

1772. Покупатель приобрел телевизор и холодильник. Вероятность того, что телевизор не выйдет из строя на протяжении гарантированного срока, составляет 0,95. Для холодильника эта вероятность равняется 0,96. Найти вероятность того, что хотя бы одна из этих покупок выдержит гарантированный срок. Готовое решение задачи

1773. Птицеферма отправила на базу 10000 яиц. Вероятность того, что каждое яйцо повредится в пути, равна 0,0002. Найти вероятность того, что на базе в отправленной партии яиц окажется три поврежденных яйца. Готовое решение задачи

1774. В первой группе 25 студентов, из них 4 – отличники, во второй группе 30 студентов, из них 6 – отличников. Из каждой группы вызывается по одному студенту. Найти вероятности события: только один студент – отличник. Готовое решение задачи

1775. Покупатель приобрел пылесос и полотер. Вероятность того, что пылесос не выйдет из строя в течение гарантийного срока, равна 0,95, для полотера эта вероятность равна 0,94. Найти вероятность того, что хотя бы один из приборов выдержит гарантийный срок. Готовое решение задачи

1776. Покупатель приобрел пылесос и полотер. Вероятность того, что пылесос не выйдет из строя в течение гарантийного срока, равна 0,95. Для полотера такая вероятность равна 0,94. Найти вероятности следующих событий:
а) оба прибора выдержат гарантийный срок;
б) ни один не выдержит гарантийный срок;
в) хотя бы один прибор выдержит гарантийный срок. Готовое решение задачи

1777. Покупатель приобрел пылесос, полотер и стиральную машину. Вероятность того, что пылесос не выйдет из строя в течение гарантийного срока, равна 0,95; для полотера – 0,9; для стиральной машины – 0,97. Найти вероятность того, что:
а) два прибора выдержат гарантийный срок;
б) три прибора выдержат гарантийный срок Готовое решение задачи

1778. Покупатель приобрел пылесос и полотер. Вероятность того, что пылесос не выйдет из строя в течение гарантийного срока, равна 0,95, для полотера такая вероятность равна 0,9. Найти вероятность того, что
а) оба прибора выдержат гарантийный срок;
б) хотя бы один выдержит гарантийный срок. Готовое решение задачи

1779. Птицеферма отправила на базу n=2500 штук яиц. Вероятность того, что каждое яйцо повредится в пути, равна p=0,0004. Найти вероятность того, что на базу прибудут m=3 непригодных яиц. Готовое решение задачи

1780. Птицеферма отправила на базу n=5000 штук яиц. Вероятность того, что каждое яйцо повредиться в пути, равна p=0,0002. Найти вероятность того, что на базу прибудут m=2 непригодных яиц. Готовое решение задачи

1781. Птицеферма отправила на базу n=4000 штук яиц. Вероятность того, что каждое яйцо повредиться в пути, равна p=0,00025. Найти вероятность того, что на базу прибудут m=1 непригодных яиц. Готовое решение задачи

1782. Птицеферма отправила на базу n=10000 штук яиц. Вероятность того, что каждое яйцо повредится в пути, равна p=0,0004. Найти вероятность того, что на базу прибудут m=3 непригодных яиц. Готовое решение задачи

1783. В двух группах обучается по 25 студентов. В первой группе сессию на «отлично» сдали 7 человек, во второй 4 человека. Из каждой группы наудачу вызывают по одному студенту. Какова вероятность того, что:
а) оба студента отличники;
б) только один отличник;
в) хотя бы один отличник. Готовое решение задачи

1784. В двух группах имеется по 25 студентов. В первой 6 отличников, во второй 4. Из каждой группы берется по одному студенту. Чему равна вероятность того что: а) Они оба не отличники? б) Хотя бы один отличник? Готовое решение задачи

1786. При изготовлении предохранителей 15% из них не удовлетворяют стандарту. Каково наивероятнейшее число стандартных предохранителей в партии из 500 штук и его вероятность? Готовое решение задачи

1787. Установлено 3 датчика движения, 1 срабатывает с вероятностью 0,96, 2 и 3 с вероятностью 0,8. Найти вероятность того, что сработают все датчики. Готовое решение задачи

1788. Для сигнализации об аварии установлены 3 независимо работающих датчиков. Вероятность срабатывания датчиков равны: p₁ = 0,8; p₂ = 0,9; p₃ = 0,7. Вычислить вероятность того, что при аварии а) сработает только один датчик, б) ни один не сработает. Готовое решение задачи

1789. Вероятность наступления некоторого события при одном испытании равна р = 0,4. Найдите вероятность того, что при 1000 испытаниях частота наступления этого события отклонится от вероятности р = 0,4 не более чем на 0,05. Готовое решение задачи

1790. При социологических опросах города N установлено, что в среднем 19% дают неискренний ответ. Сколько нужно опросить граждан города N, чтобы с вероятностью 0,94 можно было утверждать, что доля неискренних ответов среди них отклонится по абсолютной величине от вероятности получения неискреннего ответа от каждого опрашиваемого не более, чем на 0,02. Готовое решение задачи

1791. При социологических опросах города N установлено, что в среднем 15% дают неискренний ответ. Сколько нужно опросить граждан города N, чтобы с вероятностью 0,94 можно было утверждать, что доля неискренних ответов среди них отклонится по абсолютной величине от вероятности получения неискреннего ответа от каждого опрашиваемого не более, чем на 0,03. Готовое решение задачи

1792. При социологических опросах города N установлено, что в среднем 13% дают неискренний ответ. Сколько нужно опросить граждан города N, чтобы с вероятностью 0,94 можно было утверждать, что доля неискренних ответов среди них отклонится по абсолютной величине от вероятности получения неискреннего ответа от каждого опрашиваемого не более, чем на 0,01 Готовое решение задачи

1793. Согласно статистическим данным в городе N в среднем 24% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из 400 наугад выбранных новых предприятий к концу года деятельности останется не менее 90, но не более 100 предприятий? Готовое решение задачи

1794. Согласно статистическим данным в городе N в среднем 22% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из двухсот наугад выбранных новых предприятий к концу года деятельности останется не менее 40, но не более 50 предприятий? Готовое решение задачи

1795. Согласно статистическим данным в городе N в среднем 15% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из 5 наугад выбранных новых предприятий к концу года деятельности останется ровно 3? Готовое решение задачи

1796. Согласно статистическим данным в городе N в среднем 16% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из 300 наугад выбранных новых предприятий к концу года деятельности останется не менее 40, но не более 55 предприятий? Готовое решение задачи

1797. Согласно статистическим данным в городе N в среднем 20% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из 6 наугад выбранных новых предприятий к концу года деятельности останется хотя бы два? Готовое решение задачи

1798. Согласно статистическим данным в городе N в среднем 18% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из 6 наугад выбранных новых предприятий города N к концу года деятельности останется: а) ровно 4; b) более 4; с) менее 4; d) хотя бы одно предприятие? Готовое решение задачи

1799. Согласно статистическим данным в городе N в среднем 18% открывающихся новых предприятий прекращают свою деятельность в течение года. Вычислить вероятность того, что из 100 вновь открытых предприятий в городе N к концу года прекратят свою деятельность: а) 15; b) не менее 15; с) не более 21; d) не менее 13, но не более 23 предприятий. Готовое решение задачи

1800. Согласно статистическим данным в городе N в среднем 15% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из 5 наугад выбранных новых предприятий города N к концу года деятельности останется: а) ровно 3; b) более 3; с) хотя бы одно предприятие? Готовое решение задачи

Источник