Работа тока физика в чем измеряется

Работа и мощность электрического тока

теория по физике 🧲 постоянный ток

При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Ее принято называть работой тока.

Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:

Но сила тока равна:

Тогда работа тока равна:

Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.

Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:

Работа тока измеряется в Джоулях (Дж).

Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.

Закон Джоуля-Ленца

В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.

Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:

Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.

Количество теплоты измеряется в Джоулях (Дж).

Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.

Используем закон Ома и закон Джоуля—Ленца:

Мощность тока

Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.

Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).

Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:

Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:

Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.

Выразив силу тока через заряд, прошедший за единицу времени, получим:

Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:

Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.

Мощность тока внутренней цепи:

Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P₀ = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?

Используем формулу для нахождения полезной мощности:

Применим закон Ома для полной цепи:

Выразим сопротивление внешней цепи:

Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:

Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.

Подсказки к задачам

Конденсатор в цепи постоянного тока

Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.

Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.

Подсказки к задачам

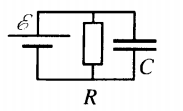
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?

Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:

Применим закон Ома:

Приравняем правые части выражений и получим:

Отсюда напряжение на конденсаторе равно:

Напряженность электрического поля равна:

Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?

Источник

Работа электрического тока: что это такое, формулы, примеры задач

В этой статье я объясню, что такое работа электрического тока, какие единицы измерения для нее используются и какие важные формулы необходимо знать.

Что такое работа электрического тока?

Давайте рассмотрим обычную батарейку. По сути, батарейка преобразует химическую энергию в электрическую энергию электронов. Если теперь подключить её в электрическую цепь, то электроны могут совершать работу, используя свою электрическую энергию, например, зажигать лампочку.

Если вы хотите узнать, сколько электрической энергии было преобразовано в другой вид энергии, то вам нужно рассчитать работу электрического тока.

Определение понятия «электрическая работа» и её единицы измерения.

Работа электрического тока [A] позволяет определить, сколько электрической энергии было или может быть преобразовано в другие виды энергии.

Когда вы рассчитываете работу электрического тока, вы знаете, сколько электрической энергии было преобразовано в другие формы энергии. А уже какие другие формы энергии могут быть — это зависит от ситуации (несколько примеров в списке ниже):

Другой важной единицей измерения является киловатт-час [кВт·ч]. Один киловатт-час равен 3 600 000 ватт-секунд или джоулей.

1 кВт·ч = 1 * 10 3 Вт·ч = 1 * 10 3 * 3600 Вт·с = 3,6 * 10 6 Вт·с = 3,6 * 10 6 Дж.

Полезный факт: а вы знали, что именно электрическую работу измеряют электросчётчики установленные в наших домах и квартирах! Электросчётчики измеряют работу электрического тока в кВт·ч.

По какой формуле вычисляется работа электрического тока?

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Чуть ниже в статье мы разберем два практических примера, которые покажут применение данных формул. Однако перед этим мы кратко рассмотрим еще несколько важных формул.

Примечание: Вы обязательно должны запомнить первые две формулы. Следующие ниже формулы менее важны, но могут быть полезны для вас при решении тех или иных задач.

Другие формулы для определения работы электрического тока.

Закон Ома для участка цепи связывает напряжение U и ток I. Это позволяет нам рассчитать электрическую работу A другим способом.

Тогда вы можете подставить эти формулы в A = U * I * t. В итоге получатся другие формулы для нахождения работы электрического тока:

Примеры задач

У вас есть батарея, подающая постоянное напряжение 12 В и ток 2,3 А. Вы используете эту батарею для освещения лампочки в течение 1 часа. Теперь вы хотите знать, какая работа электрического тока была произведена.

Мы знаем формулу для определения работы электрического тока: A = U * I * q, тогда получаем:

Чтобы дать вам представление о единицах измерения, давайте переведем результат в ватт-секунды и джоули

27,6 Вт·ч = 27,6 * 3600 Вт·с = 99360 Вт·с = 99360 Дж.

Мы знаем формулу для определения работы электрического тока: A = U * q, тогда q = A / U. Подставляя значения в формулу получаем:

Источник

Работа электрического тока. Закон Джоуля-Ленца.

Для определения работы, которая совершается током, проходящим по некоторому участку цепи, нужно воспользоваться определением напряжения: . Значит,

где А — работа тока; q — электрический заряд, который прошел за определенное время через исследуемый участок цепи. Подставив в последнее равенство формулу q = It, имеем:

Работа электрического тока на участке цепи является произведением напряжения на концах это­го участка на силу тока и на время, на протяжении которого совершалась работа.

Закон Джоуля — Ленца гласит: количество теплоты, которое выделяется в проводнике на участке электрической цепи с сопротивлением R при протекании по нему постоянного тока I в течение времени t равно произведению квадрата тока на сопротивление и время:

Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтверж­ден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которо­му удалось раскалить железную спираль, пропустив через нее электрический ток.

Из закона Джоуля — Ленца видно, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на про­воднике с наибольшим сопротивлением. Это применяется в технике, например, для распыления металлов.

При параллельном соединении каждый проводник находятся под одинаковым напряжением, но токи в них разные. Из формулы (Q = I 2 Rt) видно, что, так как, согласно закону Ома , то

Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.

Если в формуле (А = IUt) выразить U через IR, воспользовавшись законом Ома, получим Закон Джоуля — Ленца. Это лишний раз подтверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.

Источник

Работа и мощность тока

Электрическое поле на выделенном участке совершит работу

где U = Δ φ 12 обозначает напряжение. Эту работу называют работой электрического тока.

Интерпретация закона сохранения энергии. Закон Джоуля-Ленца

Закон Ома для однородного участка цепи при сопротивлении R отражает формула:

Умножим обе части выражения на I Δ t и получим соотношение:

Полученный результат является выражением закона сохранения энергии для однородного участка цепи.

Данный закон называется законом Джоуля-Ленца.

Закон носит название сразу двух известных физиков, поскольку экспериментальным путем был установлен ими обоими в независимости друг от друга.

Можно сказать проще: мощность – это работа, выполненная в единицу времени. Запишем формулу, связывающую работу тока и его мощность:

P = ∆ A ∆ t = U I = I 2 R = U 2 R

Закон Ома для полной цепи выглядит так:

Перемножим обе части выражения с Δ q = I Δ t и получим соотношение, которое будет служить выражением закона сохранения энергии для полной цепи постоянного тока:

R I 2 ∆ t + r I 2 ∆ t = δ I ∆ t = ∆ A с т

Левая часть выражения содержит Δ Q = R I 2 Δ t (тепло, которое выделяется на внешнем участке цепи за время Δ t ) и Δ Q и с т = r I 2 Δ t (тепло, которое выделяется внутри источника за такое же время).

∆ Q + Q и с т = ∆ A с т = δ I ∆ t

Необходимо отметить следующий факт: в указанное соотношение не включена работа электрического поля. Когда ток проходит по замкнутой цепи, электрическое поле работы не совершает; значит тепло производится лишь посредством сторонних сил, которые действуют внутри источника. Электрическое поле здесь выполняет перераспределение тепла между различными участками цепи.

Коэффициент полезного действия источника

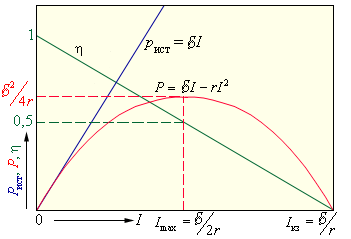
Полная мощность источника (или работа, которая производится посредством сторонних сил за единицу времени) составляет:

P и с т = δ I = δ 2 R + r

Внешняя цепь выделяет мощность:

Источник

Работа и мощность электрического тока. Закон Джоуля-Ленца

1. Электрический ток, проходя по цепи, производит разные действия: тепловое, механическое, химическое, магнитное. При этом электрическое поле совершает работу, и электрическая энергия превращается в другие виды энергии: во внутреннюю, механическую, энергию магнитного поля и пр.

Как было показано, напряжение ​ \( (U) \) ​ на участке цепи равно отношению работы ​ \( (F) \) ​, совершаемой при перемещении электрического заряда ​ \( (q) \) ​ на этом участке, к заряду: ​ \( U=A/q \) ​. Отсюда ​ \( A=qU \) ​. Поскольку заряд равен произведению силы тока ​ \( (I) \) ​ и времени ​ \( (t) \) ​ ​ \( q=It \) ​, то ​ \( A=IUt \) ​, т.е. работа электрического тока на участке цепи равна произведению напряжения на этом участке, силы тока и времени, в течение которого совершается работа.

Единицей работы является джоуль (1 Дж). Эту единицу можно выразить через электрические единицы:

​ \( [A] \) ​= 1 Дж = 1 В · 1 А · 1 с

Для измерения работы используют три измерительных прибора: амперметр, вольтметр и часы, однако, в реальной жизни для измерения работы электрического тока используют счётчики электрической энергии.

Если нужно найти работу тока, но при этом сила тока или напряжение неизвестны, то можно воспользоваться законом Ома, выразить неизвестные величины и рассчитать работу по формулам: ​ \( A=\fract \) ​ или ​ \( A=I^2Rt \) ​.

2. Мощность электрического тока равна отношению работы ко времени, за которое она совершена: ​ \( P=A/t \) ​ или ​ \( P=IUt/t \) ​; ​ \( P=IU \) ​, т.е. мощность электрического тока равна произведению напряжения и силы тока в цепи.

Единицей мощности является ватт (1 Вт): ​ \( [P]=[I]\cdot[U] \) ​; ​ \( [P] \) ​ = 1 А · 1 В = 1 Вт.

Используя закон Ома, можно получить другие формулы для расчета мощности тока: ​ \( P=\frac;P=I^2R \) ​.

Значение мощности электрического тока в проводнике можно определить с помощью амперметра и вольтметра, измерив соответственно силу тока и напряжение. Можно для измерения мощности использовать специальный прибор, называемый ваттметром, в котором объединены амперметр и вольтметр.

3. При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника, в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: ​ \( Q=A \) ​ или ​ \( Q=IUt \) ​. Учитывая, что ​ \( U=IR \) ​, ​ \( Q=I^2Rt \) ​.

Количество теплоты, выделяющееся при прохождении тока но проводнику, равно произведению квадрата силы тока, сопротивления проводника и времени.

Этот закон называют законом Джоуля-Ленца.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Силу тока в проводнике увеличили в 2 раза. Как изменится количество теплоты, выделяющееся в нём за единицу времени, при неизменном сопротивлении проводника?

1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза

2. Длину спирали электроплитки уменьшили в 2 раза. Как изменится количество теплоты, выделяющееся в спирали за единицу времени, при неизменном напряжении сети?

1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза

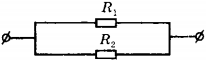
3. Сопротивления резистор ​ \( R_1 \) ​ в четыре раза меньше сопротивления резистора ​ \( R_2 \) ​. Работа тока в резисторе 2

1) в 4 раза больше, чем в резисторе 1
2) в 16 раз больше, чем в резисторе 1
3) в 4 раза меньше, чем в резисторе 1
4) в 16 раз меньше, чем в резисторе 1

4. Сопротивление резистора ​ \( R_1 \) ​ в 3 раза больше сопротивления резистора ​ \( R_2 \) ​. Количество теплоты, которое выделится в резисторе 1

1) в 3 раза больше, чем в резисторе 2
2) в 9 раз больше, чем в резисторе 2
3) в 3 раза меньше, чем в резисторе 2
4) в 9 раз меньше, чем в резисторе 2

5. Цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединенных последовательно. Лампочка станет гореть ярче, если

1) проволоку заменить на более тонкую железную
2) уменьшить длину проволоки
3) поменять местами проволоку и лампочку
4) железную проволоку заменить на нихромовую

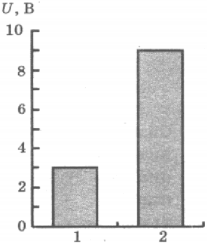
6. На рисунке приведена столбчатая диаграмма. На ней представлены значения напряжения на концах двух проводников (1) и (2) одинакового сопротивления. Сравните значения работы тока ​ \( A_1 \) ​ и ​ \( A_2 \) ​ в этих проводниках за одно и то же время.

1) ​ \( A_1=A_2 \) ​
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

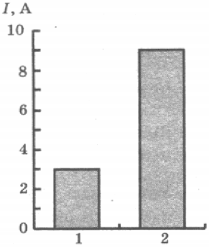
7. На рисунке приведена столбчатая диаграмма. На ней представлены значения силы тока в двух проводниках (1) и (2) одинакового сопротивления. Сравните значения работы тока \( A_1 \) ​ и ​ \( A_2 \) в этих проводниках за одно и то же время.

1) ​ \( A_1=A_2 \) ​
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

8. Если в люстре для освещения помещения использовать лампы мощностью 60 и 100 Вт, то

А. Большая сила тока будет в лампе мощностью 100 Вт.
Б. Большее сопротивление имеет лампа мощностью 60 Вт.

Верным(-и) является(-ются) утверждение(-я)

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

9. Электрическая плитка, подключённая к источнику постоянного тока, за 120 с потребляет 108 кДж энергии. Чему равна сила тока в спирали плитки, если её сопротивление 25 Ом?

1) 36 А
2) 6 А
3) 2,16 А
4) 1,5 А

10. Электрическая плитка при силе тока 5 А потребляет 1000 кДж энергии. Чему равно время прохождения тока по спирали плитки, если её сопротивление 20 Ом?

1) 10000 с
2) 2000 с
3) 10 с
4) 2 с

11. Никелиновую спираль электроплитки заменили на нихромовую такой же длины и площади поперечного сечения. Установите соответствие между физическими величинами и их возможными изменениями при включении плитки в электрическую сеть. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) электрическое сопротивление спирали
Б) сила электрического тока в спирали
B) мощность электрического тока, потребляемая плиткой

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась

12. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) работа тока
Б) сила тока
B) мощность тока

Часть 2

13. Нагреватель включён последовательно с реостатом сопротивлением 7,5 Ом в сеть с напряжением 220 В. Каково сопротивление нагревателя, если мощность электрического тока в реостате составляет 480 Вт?

Источник