Распределение гаусса что это
Распределение Гаусса
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
Содержание
Моделирование нормальных случайных величин
Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.
Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.
Статистическая проверка принадлежности нормальному распределению
Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии проверки на «нормальность»:
Заключение
Нормальное распределение наиболее часто встречается в природе, нормально распределёнными являются следующие случайные величины:
Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный). Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием предельной теоремы Ляпунова.
См. также
Полезное
Смотреть что такое «Распределение Гаусса» в других словарях:
РАСПРЕДЕЛЕНИЕ ГАУССА — син. термина распределение нормальное. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
распределение Гаусса — Gauso skirstinys statusas T sritis fizika atitikmenys: angl. Gauss distribution; gaussian distribution; Laplace Gauss distribution vok. Gauß Verteilung, f rus. Гауссово распределение, n; распределение Гаусса, n pranc. distribution de Gauss, f;… … Fizikos terminų žodynas
РАСПРЕДЕЛЕНИЕ ГАУССА — (Gaussian distribution) см. Частота распределения, значимость … Толковый словарь по медицине
Распределение Гаусса (Gaussian Distribution) — см. Частота распределения, значимость. Источник: Медицинский словарь … Медицинские термины
Континуальное распределение Гаусса — было введено в квантовой теории поля как расширение понятия распределения Гаусса для конечномерных векторов на континуальные пространства скалярных и векторных полей. Континуальное распределение активно используется в аппарате функциональных… … Википедия
ГАУССА РАСПРЕДЕЛЕНИЕ — (Гаусса закон распределения вероятностей) то же, что нормальное распределение … Большой Энциклопедический словарь
Гаусса распределение — (Гаусса закон распределения вероятностей), то же, что нормальное распределение. * * * ГАУССА РАСПРЕДЕЛЕНИЕ ГАУССА РАСПРЕДЕЛЕНИЕ (Гаусса закон распределения вероятностей), то же, что нормальное распределение (см. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ) … Энциклопедический словарь
Гаусса распределение — [Gaussian distribution] см. Нормальное распределение … Экономико-математический словарь
Новичкам. Опционы и Гауссово (нормальное) распределение.
Продолжаем грызть тему опционов по книгам Саймона и Натенберга, сегодня добрались до темы волатильность.
Волатильность — это то, что отличает торговлю фьючерсами от опционов. Кто не знает как работает волатильность, по каким законам она живет, не сможет работать с опционами. Там, где волатильность, там есть и теория вероятности, а там, где теория вероятности — сидит определенный математический аппарат.
Именно в этой точке гуманитарий опускает руки, потому что не может разобраться как работать с моделью Блэка-Шоулза, не знает элементарных понятий из теории вероятности, не знает как работает Гауссово распределение.
Будем двигаться понемногу, сегодня разберемся именно с Гауссовым распределением, я покажу на пальцах что это такое и уже потом будем постепенно углубляться в модель Блэка-Шоулза (да-да, уважаемые новички, без понимания как работает эта модель вы будете терять деньги на опционном рынке).
Что же такое Гауссово распределение, оно же распределение Гаусса-Лапласа? Это такое распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
Важно знать следующие свойства функции плотности распределения Гаусса:
С вероятностью 68,2% случайная величина не отклонится от своего математического ожидания дальше, чем 1 сигма.
С вероятностью 95,4% случайная величина не отклонится от своего математического ожидания дальше, чем 2 сигма.
С вероятностью 99,7% случайная величина не отклонится от своего математического ожидания дальше, чем 3 сигма.
Что это такое и как с этим работать трейдеру?
Есть удивительный индикатор Боллинджера, который показывает среднюю, верхнюю и нижнюю границу диапазона изменения цены актива, по умолчанию там настроен параметр 2сигма. Таким образом, если бы рынок подчинялся распределению Гаусса, то с вероятностью 95,4% цена не должна выходить за границы диапазона. Но почему же иногда она выходит? Потому что нормальное распределение по Гауссу это всего лишь математическая модель, рынки же в основе своей живут не по распределению Гаусса, на рынках есть тренд и память. Именно поэтому о каком-то случайном блуждании цены говорить не приходится, но в то же время рынки очень часто живут также и по Гауссу, мы это видим во время боковиков, когда цена хаотично движется туда-сюда, но не выходит за границы диапазона. Это как раз частный случай хаотичного движения (пропал тренд).
Более простого изложения на практике «куполообразного» распределение вероятностей я нигде не видел ранее, именно этим меня и цепанула книга Натенберга. Респект автору, умеет он всё же нетривиальные вещи объяснить простым языком.
Случайное блуждание.
Возьмем для примера игру пинбол. Шарик катится вниз через частокол штырьков. Наткнувшись на штырек, он отклоняется вправо или влево с вероятностью 50%. После этого шарик попадает на новый уровень, где натыкается на другой штырек. Наконец, внизу он падает в одну из лунок.

Движение шарика через частокол штырьков называют случайным блужданием. Как только шарик попадает в этот частокол, никто не может повлиять на его траекторию, равно как и предсказать эту траекторию.
Если бросить достаточное количество шариков, то можно получить распределение, которое называется Гауссовым — большинство шариков попадает в центр игрового поля; чем дальше лунки расположены от центра, тем меньше шариков в них оказывается. Такое распределение называется еще нормальным или колоколообразным:

Если бросить бесконечно большое количество шариков, то распределение будет описываться колоколообразной кривой, изображенной на рисунке.
Низковолатильное распределение.
Теперь давайте слегка изменим условия игры, поставив вертикальные перегородки таким образом, что теперь, наткнувшись на штырек и отклонившись влево или вправо, шарик опустится до соприкосновения со следующим штырьком не на один, а на два уровня. Если бросить достаточное количество шариков, то получится распределение, представленное кривой на рисунке (низковолатильное распределение):

Поскольку боковые движения шариков ограничены, пик этой кривой будет выше, а ее хвосты будут более узкими, чем у кривой на предыдущем рисунке. Несмотря на изменения формы, это по-прежнему кривая нормального распределения, но с несколько иными характеристиками (для тех, кто владеет математическим аппаратом — параметр эксцесс отвечает за высоту пика).
Высоковолатильное распределение.
Наконец, мы можем поставить горизонтальные перегородки так, что, попадая на следующий уровень, шарик будет каждый раз отклоняться на два штырька влево или вправо. И снова, если бросить достаточное количество шариков, то получится распределение, представленное на рисунке:

У этой кривой, которая также отражает нормальное распределение вероятностей, пик намного ниже, а хвосты убывают намного медленнее, чем у кривых на предыдущих рисунках.
Для чего нам всё это нужно было?
Пусть боковые движения шарика символизируют повышательные и понижательные изменения цены базового актива, а движение вниз — течение времени. Если предположить, что цена Ri каждый день повышается или понижается на 2500 пунктов (шаг 1 страйка), то распределение значений цены через 15 дней будет представлено на рисунке с «колоколообразной» плотностью распределения вероятностей.
Если предположить, что цена Ri повышается на 2500 пунктов каждые 2 дня, то распределение будет похоже на рисунок «низковолатильного распределения».
А если предположить, что цена Ri за день растет или падает на 5000 пунктов (2 страйка), то распределение будет напоминать рисунок «высоковолатильного распределения».
Если сегодня Ri стоит 107 500, а срок действия опциона истекает через 15 дней, то как определить стоимость 112 500 колла?
Об этом в следующих сериях.
Если такие вот топики вам заходят — ставьте лайки, жмите колокольчик, пишите каменты.
Да сопутствует вам всем удача в опционном мире!
Почему с нормальным распределением не все нормально
Нормальное распределение (распределение Гаусса) всегда играло центральную роль в теории вероятностей, так как возникает очень часто как результат воздействия множества факторов, вклад любого одного из которых ничтожен. Центральная предельная теорема (ЦПТ), находит применение фактически во всех прикладных науках, делая аппарат статистики универсальным. Однако, весьма часты случаи, когда ее применение невозможно, а исследователи пытаются всячески организовать подгонку результатов под гауссиану. Вот про альтернативный подход в случае влияния на распределение множества факторов я сейчас и расскажу.
Краткая история ЦПТ. Еще при живом Ньютоне Абрахам де Муавр доказал теорему о сходимости центрированного и нормированного числа наблюдений события в серии независимых испытаний к нормальному распределению. Весь 19 и начало 20 веков эта теорема послужила ученым образцом для обобщений. Лаплас доказал случай равномерного распределения, Пуассон – локальную теорему для случая с разными вероятностями. Пуанкаре, Лежандр и Гаусс разработали богатую теорию ошибок наблюдений и метод наименьших квадратов, опираясь на сходимость ошибок к нормальному распределению. Чебышев доказал еще более сильную теорему для суммы случайных величин, походу разработав метод моментов. Ляпунов в 1900 году, опираясь на Чебышева и Маркова, доказал ЦПТ в нынешнем виде, но только при существовании моментов третьего порядка. И только в 1934 году Феллер поставил точку, показав, что существование моментов второго порядка, является и необходимым и достаточным условием.
ЦПТ можно сформулировать так: если случайные величины независимы, одинаково распределены и имеют конечную дисперсию отличную от нуля, то суммы (центрированные и нормированные) этих величин сходятся к нормальному закону. Именно в таком виде эту теорему и преподают в вузах и ее так часто используют наблюдатели и исследователи, которые не профессиональны в математике. Что в ней не так? В самом деле, теорема отлично применяется в областях, над которыми работали Гаусс, Пуанкаре, Чебышев и прочие гении 19 века, а именно: теория ошибок наблюдений, статистическая физика, МНК, демографические исследования и может что-то еще. Но ученые, которым не достает оригинальности для открытий, занимаются обобщениями и хотят применить эту теорему ко всему, или просто притащить за уши нормальное распределение, где его просто быть не может. Хотите примеры, они есть у меня.
Коэффициент интеллекта IQ. Изначально подразумевает, что интеллект людей распределен нормально. Проводят тест, который заранее составлен таким образом, при котором не учитываются незаурядные способности, а учитываются по-отдельности с одинаковыми долевыми факторами: логическое мышление, мысленное проектирование, вычислительные способности, абстрактное мышление и что-то еще. Способность решать задачи, недоступные большинству, или прохождение теста за сверхбыстрое время никак не учитывается, а прохождение теста ранее, увеличивает результат (но не интеллект) в дальнейшем. А потом филистеры и полагают, что «никто в два раза умнее их быть не может», «давайте у умников отнимем и поделим».
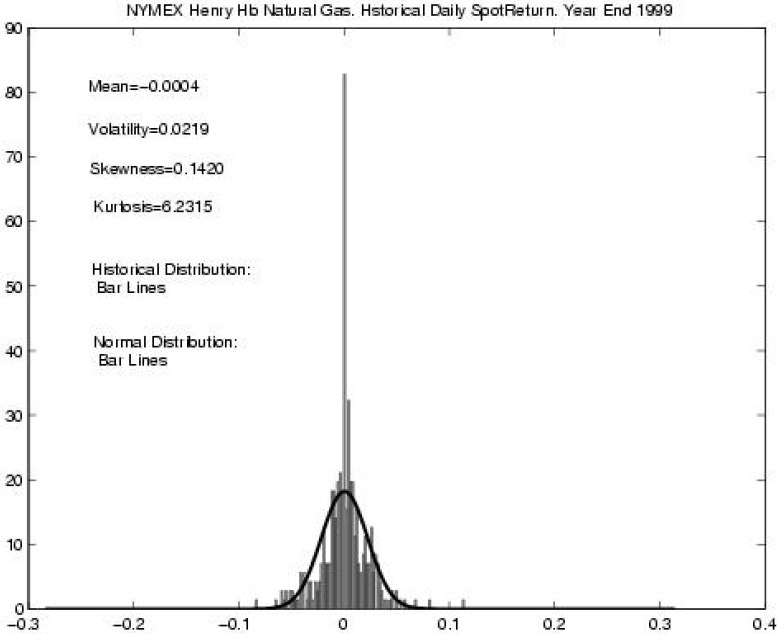
Второй пример: изменения финансовых показателей. Исследования изменения курса акций, котировок валют, товарных опционов требует применения аппарата математической статистики, а особенно тут важно не ошибиться с видом распределения. Показательный пример: в 1997 году нобелевская премия по экономике была выплачена за предложение модели Блэка — Шоулза, основанной на предположении нормальности распределения прироста фондовых показателей (так называемый белый шум). При этом авторы явно заявили, что данная модель нуждается в уточнении, но всё, на что решилось большинство дальнейших исследователей – просто добавить к нормальному распределению распределение Пуассона. Здесь, очевидно, будут неточности при исследовании длинных временных рядов, так как распределение Пуассона слишком хорошо удовлетворяет ЦПТ, и уже при 20 слагаемых неотличимо от нормального распределения. Гляньте на картинку снизу (а она из очень серьезного экономического журнала), на ней видно, что, несмотря на достаточно большое количество наблюдений и очевидные перекосы, делается предположение о нормальности распределения.
Весьма очевидно, что нормальными не будет распределения заработной платы среди населения города, размеров файлов на диске, населения городов и стран.
Общее у распределений из этих примеров – наличие так называемого «тяжелого хвоста», то есть значений, далеко лежащих от среднего, и заметной асимметрии, как правило, правой. Рассмотрим, какими еще, кроме нормального могли бы быть такие распределения. Начнем с упоминаемого ранее Пуассона: у него есть хвост, но мы же хотим, чтобы закон повторялся для совокупности групп, в каждой из которых он наблюдается (считать размер файлов по предприятию, зарплату по нескольким городам) или масштабировался (произвольно увеличивать или уменьшать интервал модели Блэка — Шоулза), как показывают наблюдения, хвосты и асимметрия не исчезают, а вот распределение Пуассона, по ЦПТ, должно стать нормальным. По этим же соображениям не подойдут распределения Эрланга, бета, логонормальное, и все другие, имеющие дисперсию. Осталось только отсечь распределение Парето, а вот оно не подходит в связи с совпадением моды с минимальным значением, что почти не встречается при анализе выборочных данных.
Распределения, обладающее необходимыми свойствами, существуют и носят название устойчивых распределений. Их история также весьма интересна, а основная теорема была доказана через год после работы Феллера, в 1935 году, совместными усилиями французского математика Поля Леви и советского математика А.Я. Хинчина. ЦПТ была обобщена, из нее было убрано условие существования дисперсии. В отличие от нормального, ни плотность ни функция распределения у устойчивых случайных величин не выражаются (за редким исключением, о котором ниже), все что о них известно, это характеристическая функция (обратное преобразование Фурье плотности распределения, но для понимания сути это можно и не знать).
Итак, теорема: если случайные величины независимы, одинаково распределены, то суммы этих величин сходятся к устойчивому закону.
Теперь определение. Случайная величина X будет устойчивой тогда и только тогда, когда логарифм ее характеристической функции 
где 
В самом деле, ничего сильно сложного здесь нет, просто надо объяснить смысл четырех параметров. Параметры сигма и мю – обычные масштаб и смещение, как и в нормальном распределении, мю будет равно математическому ожиданию, если оно есть, а оно есть, когда альфа больше одного. Параметр бета – асимметрия, при его равенстве нулю, распределение симметрично. А вот альфа это характеристический параметр, обозначает какого порядка моменты у величины существуют, чем он ближе к двум, тем больше распределение похоже на нормальное, при равенстве двум распределение становиться нормальным, и только в этом случае у него существуют моменты больших порядков, также в случае нормального распределения, асимметрия вырождается. В случае, когда альфа равна единице, а бета нулю, получается распределение Коши, а в случае, когда альфа равна половине, а бета единице – распределение Леви, в других случаях не существует представления в квадратурах для плотности распределения таких величин.
В 20 веке была разработана богатая теория устойчивых величин и процессов (получивших название процессов Леви), показана их связь с дробными интегралами, введены различные способы параметризации и моделирования, несколькими способами были оценены параметры и показана состоятельность и устойчивость оценок. Посмотрите на картинку, на ней смоделированная траектория процесса Леви с увеличенным в 15 раз фрагментом.
Именно занимаясь такими процессами и их приложением в финансах, Бенуа Мандельброт придумал фракталы. Однако не везде было так хорошо. Вторая половина 20 века прошла под повальным трендом прикладных и кибернетических наук, а это означало кризис чистой математики, все хотели производить, но не хотели думать, гуманитарии со своей публицистикой оккупировали математические сферы. Пример: книга «Пятьдесят занимательных вероятностных задач с решениями» американца Мостеллера, задача №11:
Авторское решение этой задачи, это просто поражение здравого смысла:
Такая же ситуация и с 25 задачей, где даются ТРИ противоречащих ответа.
Но вернемся к устойчивым распределениям. В оставшейся части статьи я попытаюсь показать, что не должно возникать дополнительных сложностей при работе с ними. А именно, существуют численные и статистические методы, позволяющие оценивать параметры, вычислять функцию распределения и моделировать оные, то есть работать так же, как и с любым другим распределением.
Моделирование устойчивых случайных величин. Так как все познается в сравнении, то напомню сначала наиболее удобный, с точки зрения вычислений, метод генерирования нормальной величины (метод Бокса – Мюллера): если 

получится стандартная нормальная величина.
Теперь зададим заранее альфу и бету, пусть V и W, независимые случайные величины: V равномерно распределена на 



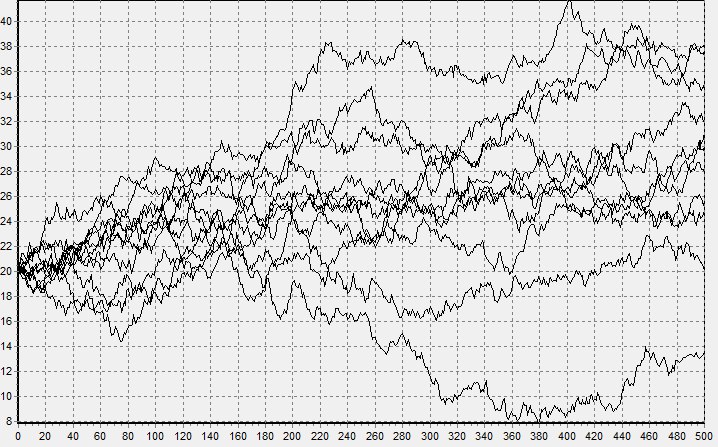
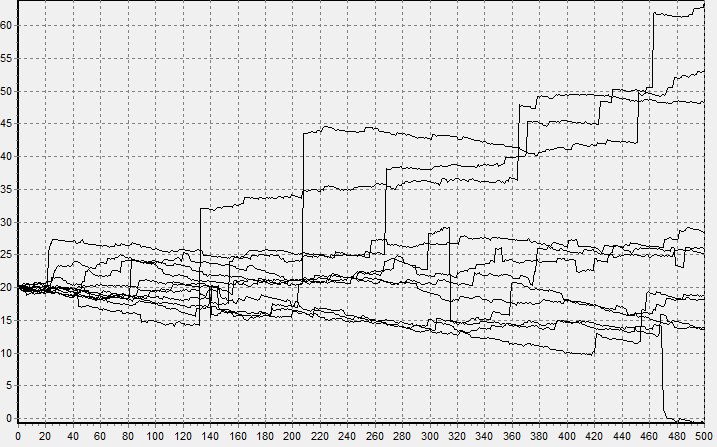
получим устойчивую случайную величину, для которой мю равна нулю, а сигма единице. Это так называемая стандартная устойчивая величина, которую для общего случая (при альфа не равном единице), просто достаточно помножить на масштаб и прибавить смещение. Да, соотношение сложнее, но оно все равно достаточно простое, чтобы его использовать даже в электронных таблицах (Ссылка). На рисунках снизу показаны траектории моделирования модели Блэка — Шоулза сперва для нормального, а затем для устойчивого процесса.
Можете поверить, график изменения цен на биржах больше похож на второй.
Оценка параметров устойчивого распределения. Так как вставлять формулы на хабре достаточно сложно, я просто оставлю ссылку на статью, где подробно разбираются всевозможные методы для оценки параметров, или на мою статью на русском языке, где приводятся только два метода. Также можно найти замечательную книгу, в которой собрана вся теория по устойчивым случайным величинам и их приложениям (Zolotarev V., Uchaikin V. Stable Distributions and their Applications. VSP. M.: 1999.), или ее чисто научный русский вариант (Золотарев В.М. Устойчивые одномерные распределения. – М.: Наука, Главная редакция физико-математической литературы, 1983. – 304 с.). В этих книгах также присутствуют методы для вычисления плотности и функции распределения.
В качестве заключения могу лишь порекомендовать, при анализе статистических данных, когда наблюдается асимметрия или значения, сильно превосходящие ожидаемые, спрашивать самих себя: «правильно ли выбран закон распределения?» и «а все ли с нормальным распределением нормально?».
Открытие про Гауссово распределение, или тайна Иоганна Карла Фридриха Гаусса.
Ну так вот. Есть такая штука – Гауссово распределение. Оно очень часто встречается, оно повсюду.
Практически, куда ни плюнь – там гауссово распределение.
И это, между прочим, не метафора! Если начать куда-нибудь плевать, то плевки будут распределятъся именно по гауссу.
Поэтому не будет преувеличением сказать, что куда ни плюнь – там гауссово распределение.
Гаусово распределение, или оно еще называется „нормальное распределение“, описывается страшной формулой:
А график его выглядит как колокольчик, вот так:
Ну и возникает вопрос – почему совершенно разные процессы, такие как плевание в потолок, траектория ракеты,
или посещаемость избирательных участков (кроме, конечно, российских), описываются именно этой формулой?
Даже два вопроса возникает:
1. Какое общее свойство у всех этих процессов?
Ведь случайный процесс может быть любым, распределение может быть вообще произвольным.
Не может же так случайно получиться, что у кучи совершенно различных процессов распределение описывается
одной и той же формулой. Значит, должно быть у них какое-то общее свойство, которое именно этой формулой и
описывается.
Причем, это должно быть какое-то ОЧЕНЬ ПРОСТОЕ свойство, раз куча совершенно разных процессов им обладает.
Чтобы ответить на оба эти вопроса, возьмем да и построим это Гауссово распределение своими руками.
Но позже. Для начала поясним – о чем вообще речь. 🙂
Есть у нас какая-то величина, назовем ее X. Ну, например, температура в комнате в градусах Цельсия.
Она в течении дня принимает разные значения. Например, <18°, 19°, 18°, 18°, 19°, 20° >.
Все эти значения можно графически изобразить в виде «гистограммы“:
Или можно отображать значения горизонтальными черточками:
Это дело вкуса, обычно используются горизонтальные черточки.
Если X принимает нецелые значения, например, 18.2°, то их округляют до целых.
Вот все эти графики и называются “распределением величины X“. Они просто показывают – как часто X принимает то или иное значение.
Понятно, что распределение может быть любой формы. Но есть такие формы, которые встречаются часто, и у них есть свои названия.
Например: Гауссово (или нормальное) распределение, распределение Пуассона, равномерное распределение, распределение Ландау, и еще всякие разные.
Все они исследованы Гауссом, Пуассоном и Ландау соответственно, и их графики описаны аналитически, в виде формул.
Ну и вот интересно – почему это одни распределения встречаются чаще, чем другие.
Взять, например, равномерное распределение.
Равномерное распределение означает, что величина X распределена равномерно – все значения одинаково вероятны.
Формула у него предельно простая:
Казалось бы, это равномерное распределение должно быть самым распространенным.
Ан нет, не тут то было. Куда ни плюнь – все везде распределено по Гауссу, и описывается жуткой формулой.
Гаусс своими руками.
Чтобы понять – что такое Гауссово распределение, почему оно именно такое, и почему оно так часто встречается, возьмем да и построим этого Гаусса своими руками.
# Осторожно.
# Дальнейший текст содержит секретную информацию, не известную ни одному аспиранту,
# не говоря уже о профессорах и академиках
# Читая дальнейший текст, вы подписываетсесь под тем, что читаете его на свой страх и риск.
# Автор не несет никакой ответственности ни за что, и ниибет.
Теперь рисуем гистограмму. Наша X распределена вот так:
Возьмем другую случайную величину X1, которая точно так же распределена, и при этом НЕЗАВИСИМА от X.
Например, будем кидать еще одну монетку.
Добавим ее к нашему X и посмотрим как изменится распределение. Гистограмма суммы двух величин (X+X1) выглядит так:
Прикольно, да? У суммы края разъехались и появился пик в нуле.
Понятно, почему так получается.
Уже, наверное, понятно, что будет дальше. Добавим еще одну величину X2, так же распределенную:
Досыпeм туда еще случайных величин.
Сумма 20-ти случайных величин выглядит так:
Получился всеми любимый Гаусс, описываемый жуткой формулой.
(Для сравнения, красная линия показывает идеальный Гаусс, нарисованный по формуле.)
Вот и все, чистая арифметика.
Именно поэтому Гаусс так часто встречается.
И наоборот, если нечто распределено по Гауссу, то можно уверенно сказать,
что это нечто является сложным процессом, в который вовлечено много независимых факторов.
Правильный ответ такой – в сумме будет Гаусс. Когда слагаемых много, то эффект от суммирования перевешивает
индивидуальные особенности распределений, и в итоге получается Гаусс.
Например, возьмем X распределенный по Ландау
(вообще, у Ландау бесконечный хвост вправо, но я его отбросил и сдвинул все немного влево,
чтобы центр распределения оказался в нуле).
Вот такая штука получилась:
Ландау неудобно тем, что оно совсем несимметричное. Ну ничего.
Сложим два Ландау:
Ага! 🙂 Правый хвост поджался, уже похоже на Гаусс, но не совсем.
Теперь сложим сразу 100 Ландау:
Ну уже почти.
Возьмем 1000 Ландау:
Уверен, что ни один ученый из тех, кто пользуется Гауссианам, не знает что это такое.
Хотя, может и есть где-то пара специалистов по теории вероятностей, постигших тайну нормального распределения,
и по секрету передающих ее из поколения в поколение, кто знает.