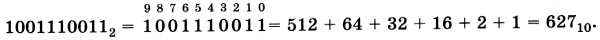Равно количеству цифр составляющих алфавит системы счисления что это
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Представление чисел в позиционных системах счисления
Информатика. 10 класса. Босова Л.Л. Оглавление
§10. Представление чисел в позиционных системах счисления
10.1. Общие сведения о системах счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов свидетельствуют о том, что первоначально число предметов отображали равным количеством каких-либо значков (бирок): зарубок, чёрточек, точек. Такая система записи чисел называется единичной (унарной), т. к. любое число в ней образуется путём повторения одного знака, символизирующего единицу.
Подумайте, где в наши дни можно найти отголоски унарной системы счисления.
Унарная система — не самый удобный способ записи чисел: записывать таким способом большие значения утомительно, да и сами записи при этом получаются очень длинными. С течением времени возникли иные, более удобные и экономичные системы счисления.
Система счисления или нумерация — это способ записи (обозначения) чисел.
Система счисления — это знаковая система, в которой числа записываются по определённым правилам с помощью символов некоторого алфавита, называемых цифрами. Количество цифр, составляющих алфавит, называется его размерностью или мощностью.
Различают непозиционные и позиционные системы счисления.
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения этой цифры в числе.
Примером непозиционной системы, которая сохранилась до наших дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежали знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две скрещённые ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 стали применять первые буквы соответствующих латинских слов (centum — сто, demimille — половина тысячи, mille — тысяча).
Чтобы записать число, римляне разлагали его на сумму тысяч (М), полутысяч (D), сотен (С), полусотен (L), десятков (X), пятёрок (V), единиц (I). Например, десятичное число 128 представляется следующим образом:
CXXVIII = 100 + 10 + 10 + 5 + 1 + 1 + 1
(одна сотня, два десятка, пять, три единицы).
Для записи промежуточных чисел римляне использовали не только сложение, но и вычитание. При этом применялось следующее правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Например, XI обозначает 11, а IX обозначает 9.
Римскими цифрами пользовались очень долго. Ещё 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). Римская система счисления сегодня используется в основном для наименования знаменательных дат, томов, разделов и глав в книгах.
Подумайте, почему римскую систему счисления нельзя считать полностью непозиционной.
Непозиционные системы счисления имеют ряд существенных недостатков:
• существует постоянная потребность введения новых знаков для записи больших чисел;
• невозможно представлять дробные и отрицательные числа;
• сложно выполнять арифметические операции, т. к. не существует алгоритмов их выполнения.
Всех перечисленных недостатков лишены позиционные системы счисления.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (места, позиции) в записи числа.
Например, используемая повсеместно десятичная система счисления — позиционная. Рассмотрим число 555. Цифра 5, стоящая в записи этого числа на первом месте, обозначает количество сотен и соответствует числу 500; цифра, стоящая посередине, обозначает 5 десятков (50); последняя цифра 5 соответствует пяти единицам. Исходное число можно представить в виде суммы:
555 = 500 + 50 + 5.
Потребовалось много тысячелетий, чтобы люди научились называть и записывать числа так, как это делаем мы с вами. Начало этому было положено в Древнем Египте и Вавилоне, а завершили дело индийские математики в V-VII веках нашей эры. Важным достижением индийской науки было введение особого обозначения для пропуска разрядов — нуля. Арабы, познакомившись с этой нумерацией первыми, по достоинству её оценили, усвоили и перенесли в Европу. Получив название арабской, эта система в XII веке нашей эры распространилась по всей Европе. И так как эта система счисления проще и удобнее остальных, быстро их вытеснила.
Французский математик Пьер Симон Лаплас (1749-1827) оценил «открытие» позиционной системы такими словами: «Мысль выражать все числа немногими знаками, придавая им кроме значения по форме ещё значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна».
10.2. Позиционные системы счисления
Существует бесконечно много позиционных систем счисления. Каждая из них определяется целым числом q > 1, называемым основанием системы счисления. Основание определяет (даёт) название системы счисления: двоичная, троичная, восьмеричная, шестнадцатеричная, g-ичная и т. д. Можно говорить «система счисления с основанием q» (табл. 3.1).
Основное достоинство любой позиционной системы счисления — возможность записи произвольного числа ограниченным количеством символов. Для записи чисел в позиционной системе счисления с основанием q нужен алфавит из q цифр: 0, 1, 2, …, g — 1.
Таблица 3.1
Основания и алфавиты систем счисления
В g-ичной системе счисления q единиц какого-либо разряда образуют единицу следующего разряда.
Целое число без знака А в g-ичной системе счисления представляется в виде конечной суммы степеней числа q — суммы разрядных слагаемых:
• q — основание системы счисления;
• аi — цифры, принадлежащие алфавиту данной системы счисления (0 ≤ аi ≤ q — 1);
• q i — весовой коэффициент разряда.
Последовательность чисел, каждое из которых задаёт «вес» соответствующего разряда, называется базисом позиционной системы счисления.
Свёрнутой формой записи числа мы пользуемся в повседневной жизни, иначе её называют естественной формой или цифровой.
Развёрнутая форма записи чисел также всем хорошо известна. Ещё в начальной школе дети учатся записывать числа в виде суммы разрядных слагаемых. Например:
125 248 = 1 • 100 000 + 2 • 10 000 + 5 • 1 000 + 2 • 100 + 4 • 10 + 8 • 1.
Если представить разряды в виде степей основания, то получим:
Аналогичным образом представляются и дроби:
Иногда бывает полезно преобразовать развёрнутую форму записи числа так, чтобы избежать возведения основания системы счисления в степени.
Например, можно записать:
125 248 = 1 • 10 5 + 2 • 10 4 + 5 • 10 3 + 2 • 10 2 + 4 • 10 1 + 8 • 10 0 = ((((1 • 10 + 2) • 10 + 5) • 10 + 2) • 10 + 4) • 10 + 8;
Такую форму представления числа называют разложением по схеме Горнера.
Изучая десятичную систему счисления с раннего возраста и используя её в повседневной практике, многие люди не догадываются о существовании других систем счисления.
Но так ли хороша десятичная система счисления? Великий французский математик и естествоиспытатель Блез Паскаль (1623-1662) писал: «Десятичная система построена довольно неразумно, конечно, в соответствии с людскими обычаями, а вовсе не с требованиями естественной необходимости, как склонно думать большинство людей». В ряде теоретических и практических задач некоторые системы счисления, отличные от десятичной, имеют определённые преимущества.
Первые механические счётные машины были разработаны на основе десятичной системы счисления. Для реализации десяти устойчивых состояний в них использовались сложные системы зубчатых колёс (рис. 3.1). Такие машины были очень громоздки, занимали много места.
Рис. 3.1. Механизм передачи десятков в арифмометре П.Л. Чебышёва
Так, если бы проект Аналитической машины Ч. Беббиджа — механического прототипа появившихся спустя столетие ЭВМ — был реализован, то по размерам такая машина сравнялась бы с локомотивом. В 1937 году немецкий инженер К. Цузе создал вычислительную машину, основанную на принципах действия аналитической машины Ч. Беббиджа. Она была механической, но работала на основе двоичной системы счисления, что позволило значительно уменьшить её размеры: машина занимала всего 2 м 2 на столе в квартире изобретателя!
В наши дни большой практический интерес представляют двоичная, троичная, восьмеричная и шестнадцатеричная системы счисления.
10.3. Перевод чисел из g-ичной в десятичную систему счисления
Перевод числа, записанного в системе счисления с основанием q, в десятичную систему счисления основан на использовании развёрнутой формы записи чисел (рис. 3.2).
Рис. 3.2. Перевод числа из g-ичной системы счисления в десятичную
Для перевода числа Aq в десятичную систему счисления достаточно:
1) записать развёрнутую форму числа Aq;
2) представить все числа, фигурирующие в развёрнутой форме, в десятичной системе счисления;
3) вычислить значение полученного выражения по правилам десятичной арифметики.
Переведём числа 2123, 1235 и 12А16 в десятичную систему счисления:
2123 = 2 • 3 2 + 1 • 3 1 + 2 • 3 0 = 2 • 9 + 1 • 3 + 2 • 1 = 2310;
1235 = 1 • 5 2 + 2 • 5 1 + 3 • 5 0 = 2 • 25 + 2 • 5 + 3 • 1 = 6310;
12А16 = 1 • 16 2 + 2 • 16 1 + А • 16 0 = 1 • 256 + 2 • 16 + 10 • 1 = 29810.
Перевод в десятичную систему счисления целых двоичных чисел будет значительно проще, если вспомнить и использовать уже знакомую вам таблицу степеней двойки:
Для перевода двоичного числа в десятичную систему счисления можно воспользоваться схемой Горнера:
1) 1 • 2 = 2 — возьмем 1, соответствующую самому старшему разряду числа, и умножим её на 2;
2) 2 + 0 = 2 — прибавим следующую цифру;
3) 2 • 2 = 4 — умножим результат на 2;
4) 4 + 0 — 4 — прибавим следующую цифру;
5) 4 • 2 = 8 — умножим результат на 2;
6) 8 + 1 = 9 — прибавим следующую цифру;
7) 9 • 2 = 18 — умножим результат на 2;
8) 18 + 1 = 19 — прибавим следующую цифру;
9) 19 • 2 = 38 — умножим результат на 2;
10) 38 + 1 = 39 — прибавим следующую цифру;
11) 39 • 2 = 78 — умножим результат на 2;
12) 78 + 0 = 78 — прибавим следующую цифру;
13) 78 • 2 = 156 — умножим результат на 2;
14) 156 + 0 = 156 — прибавим следующую цифру;
15) 156 • 2 = 312 — умножим результат на 2;
16) 312 + 1 = 313 — прибавим следующую цифру;
17) 313 • 2 = 626 — умножим результат на 2;
18) 626 + 1 = 627 — прибавим последнюю цифру.
Рассмотрим несколько примеров решения задач.
Пример 1. Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления.
Запишем условие задачи иначе: 212g = 5710, q > 2. Представим в виде суммы разрядных слагаемых:
212q = 2 • q 2 + 1 • q 1 + 2 • q 0 =2q 2 + q + 2 = 5710.
Решим уравнение: 2g 2 + q + 2 = 57.
Так как основание системы счисления должно быть натуральным числом, то q — 5.
Пример 2. Все пятибуквенные слова, составленные из пяти букв А, И, Р, С, Т, записаны в алфавитном порядке.
Необходимо найти ответы на два вопроса.
1. На каком месте от начала списка стоит слово ИСТРА?
2. Сколько всего слов в этом списке?
Введём следующие обозначения: А — О, И — 1, Р — 2, С — 3, Т — 4. Перепишем в новых обозначениях исходный список:
Теперь перед нами последовательность чисел от 0 до 44444, записанных в пятеричной системе счисления. При этом на 1-м месте в этой последовательности находится 0, на 2-м месте — 1, на 3-м месте — 2 и т. д. Это значит, что само число на единицу меньше того места (номера), которое оно занимает в последовательности.
Представив слово ИСТРА в новых обозначениях, получим 134205. Переведём это пятеричное число в десятичную систему счисления:
134205 = 1 • 5 4 + 3 • 5 3 + 4 • 5 2 + 2 • 5 1 + 0 • 5 0 = 625 + 375 + 100 + 10 = 111010.
Это число находится в списке на 1111-м месте.
Чтобы выяснить, сколько всего слов в списке, запишем его самое последнее слово: ТТТТТ. Ему соответствует число 444445.
444445 = 4 • 5 4 + 4 • 5 3 + 4 • 5 2 + 4 • 5 1 + 4 • 5 0 = 312410.
В списке это число стоит на 3125-м месте.
Вспомните о комбинаторике и предложите другой способ подсчёта количества слов в нашем списке.
Пример 3. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 60, запись которых в четверичной системе счисления оканчивается на 31.
В четверичной системе счисления используются цифры 0, 1, 2 и 3; число представляется в виде суммы разрядных слагаемых:
Из этой таблицы видно, что интересующие нас числа (≤ 60) не будут более чем трёхзначными. С учётом того что их запись заканчивается на 31, определим первую цифру (k):
k • 16 + 3 • 4 + 1 ≤ 60, k • 16 ≤ 47, k ∈ <0, 1, 2>.
САМОЕ ГЛАВНОЕ
Система счисления — это способ записи (обозначения) чисел. Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (места, позиции) в записи числа.
Существует бесконечно много позиционных систем счисления. Каждая из них определяется целым числом q > 1, называемым основанием системы счисления. Для записи чисел в позиционной системе счисления с основанием q нужен алфавит из q цифр: 0, 1, 2, q — 1.
Для перевода числа Aq в десятичную систему счисления достаточно:
1) записать развёрнутую форму числа Аg;
2) представить все числа, фигурирующие в развёрнутой форме, в десятичной системе счисления;
3) вычислить значение полученного выражения по правилам десятичной арифметики.
Вопросы и задания
1. Что такое система счисления? Какие классы систем счисления принято выделять?
2. Дайте определение позиционной системы счисления. Что называется алфавитом системы счисления? Что называется базисом позиционной системы счисления? Что называется основанием позиционной системы счисления?
3. Сколько цифр используется в системе счисления с основанием 2, 3, 5, 8, 16, 100, q?
4. Какая форма записи числа называется развёрнутой?
5. Запишите в развёрнутой форме числа:
6. Воспользуйтесь схемой Горнера для представления чисел:
7. Вычислите десятичные эквиваленты следующих чисел:
8. Существует ли треугольник, длины сторон которого выражаются числами 128, 1223 и 110112?
9. Укажите целые десятичные числа, принадлежащие следующим числовым промежуткам:
10. Найдите основание х системы счисления, если известно:
11. Десятичное число 63 в некоторой системе счисления записывается как 120. Определите основание системы счисления.
12. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству 9D16
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Общие сведения о системах счисления
Современные люди воспринимают цифры как данность. Ведь людей учат считать с ранних лет. Поэтому ни у кого не возникает проблем с подсчетом оставшиеся наличности, пройденных шагов, дней до важного события.
Но как именно люди научились считать? Когда это произошло?
Учиться считать люди начали с незапамятных времен, а учителем у них была сама жизни.
Древние люди наблюдая за окружающие их природой от которой зависела их жизнь и процветание из большого разнообразия предметов и вещей изначально научились выделять всего лишь отдельные предметы.
Из стада животных одно животное, из косяка рыб одну рыбу. Изначально они смогли определить это отношение как один и много умение.
Вести подсчет играла большую роль выживания не только одного человека, но и всего его племени до того, как научиться считать наши предки использовали конечности пальцы рук и ног и окружавшие их предметы палочки камушки.
Потребности в ведение счета крупных чисел дали толчок к появлению письменного счета так как бумагу еще не производили и не знали, как это делать подсчеты проводились посредством зарубин на костях животных и полках или узелками на веревках или письма на глиняных дощечках.
Такой способ записи чисел назывался унарной системе счисления

Унарная система счисления это простейшая и самая древняя система, в которой для записи любых чисел используется всего один символ палочка узелок зарубка камушек.
Длина записи числа при таком кодировании прямо связано с его величиной что роднит этот способ с геометрическим представлением чисел введя отрезков.
Именно унарная система лежит фундаменте арифметики и именно она до сих пор вводит первоклассников в мир счет.
Унарные системы еще называют системами бирок.
Давайте дадим определение системе счисления.
Система счисления — это знаковая система, в которой приняты определенные правила записи чисел знаки с помощью которых записываются числа называются цифрами, а их совокупность алфавитом системы счисления.
Можно выделить следующие виды систем счисления
1. унарная система счисления
2. непозиционные системы
3. позиционные системы
Система счисления называется не позиционной если количественный эквивалент количественное значение цифры в числе не зависит от ее положения в записи числа.
Примером непозиционные системы счисления является римская система у римлян были специальные обозначения для чисел 1, 5, 10, 50, 100, 500 и 1000 римские цифры имели такой вид:
Обозначая цифры, римляне записывали столько цифр чтобы, их сумма давала нужное число.
Например, число 7 они записывали VII
число 362 — CCCLXII
Как видите сначала идут большие цифры, а потом поменьше, но иногда римляне писали меньшую цифру перед большей это означало что нужно не складывать и вычитать.
Например, число 4 обозначалось IV, а число 9 — IX
Запись XC означало число 90
В позиционной системе счисления как раз все наоборот величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Основании позиционной системы счисления равно количеству цифр, составляющих ее алфавит.
Алгоритмические числа образуется в ней следующим образом значение цифр умножаются на веса соответствующих разрядов и все полученные значения складываются. Это отчетливо прослеживается в числительных русского языка. Три ста пять десят семь.
Основанием позиционной системы счисления может служить любое натуральное число q > 1.
Алфавит десятичные системы составляют цифры
Определение. Система счисления или нумерация — это способ записи (обозначения) чисел.
Определение. Символы, при помощи которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления. Количество цифр, составляющих алфавит, называется его размерностью.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от ее положения в записи числа.
В позиционных системах счисления значения числа образуется путем умножения значения цифр на «веса» соответствующих разрядов и, затем, все полученные произведения складываются. Например,
504710 = 5 • 1000 + 0 • 100 + 4•10 + 7 • 1
D4А516 = D • 4096 + 4 • 256 + A • 16 + 5 • 1
11012 = 1 • 8 + 0 • 4 + 0 • 2 + 1 • 1
Базис, алфавит и основание позиционной системы счисления
Определение. Последовательность чисел, каждое из которых задает «вес» соответствующего разряда, называется базисом позиционной системы счисления.
Определение. Позиционную систему счисления называют традиционной, если ее базис образуют члены геометрической прогрессии, а значения цифр есть целые неотрицательные числа.
Определение. Знаменатель Р геометрической прогрессии, члены которой образуют базис традиционной системы счисления, называется основанием этой системы счисления. Традиционные системы счисления с основанием Р иначе называют Р-ичными…
В Р-ичных системах размерность алфавита равна основанию системы счисления.
Основанием Р-ичной системы счисления может быть любое натуральное число, большее единицы. Системой счисления с минимальным основанием является двоичная система.
Последовательность чисел может являться базисом позиционной системы счисления только тогда, когда в соответствующей этому базису системе может быть представлено любое число (если система предназначена только для нумерации целых чисел, то любое целое число).
Договоренности о формах записи цифр
В качестве цифр систем счисления могут быть использованы любые символы.
В математике придерживаются следующих договоренностей в отношении вида используемых, цифр:
Copyright © 2014-2021, Урок информатики
Все права защищены
Равно количеству цифр составляющих алфавит системы счисления что это
Египетская система счисления
Древнеславянская система счисления
Вавилонская система счисления
Унарная система счисления
Непозиционная система счисления
Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Позиционная система счисления
Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от её положения в записи числа.
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Десятичная система счисления
Цифры 1234567890 сложились в Индии около 400 г. н. э.
Арабы стали пользоваться подобной нумерацией около 800 г. н. э.
Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
Такая запись числа называется развёрнутой формой записи.
Примеры записи чисел в развёрнутой форме:
2012=2 ´ 10 3 +0 ´ 10 2 +1 ´ 10 1 +2 ´ 10 0
14351,1=1 ´ 10 4 +4 ´ 10 3 +3 ´ 10 2 +5 ´ 10 1 +1 ´ 10 0 +1 ´ 10 –1