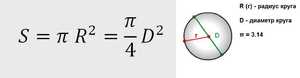Размер поперечного сечения элемента h что это
iSopromat.ru
Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины. 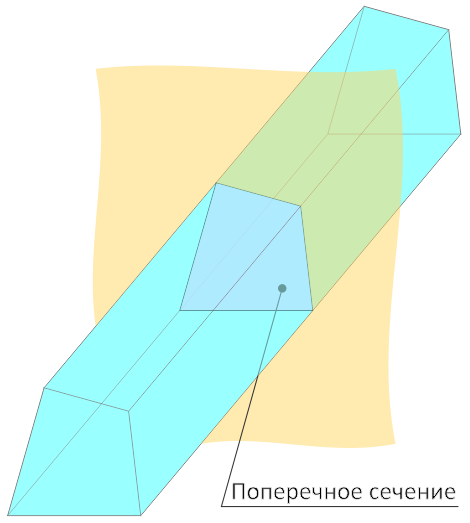
Сечение может иметь простую или сложную форму, а также быть составным.
Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Пример:
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением. 
Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто. 
В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым. 
Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Длина поперечного сечения
Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками. 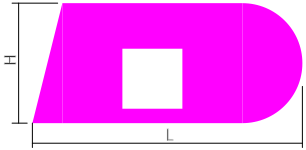
Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.
Ширина сечения определяется аналогично, но обозначается буквой H или h.
Различают два основных вида расчета площади сечений:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Уточнение размеров поперечного сечения
Содержание
2. Компоновка балочного панельного сборного перекрытия………………….3
3. Предварительные размеры поперечного сечения элементов и расчетные сопротивления материалов……………………………………………………….4
4. Расчет неразрезного ригеля……………………………………………………5
4.2 Уточнение размеров поперечного сечения…………………………. 7
4.3 Подбор продольной арматуры……………………………………… 10
4.4 Подбор поперечной арматуры……………………………………….19
4.6 Эпюра материалов (арматуры)………………………………………23
4.7 Определение расстояния от точки теоретического обрыва до торца обрываемого стержня……………………………………………………………26
5.1 Вычисление нагрузок………………………………………………. 28
Список использованной литературы………………………………………….34
Исходные данные
Компоновка балочного панельного сборного перекрытия
При заданной сетке колонн компоновка перекрытия включает в себя определение направления ригелей и раскладку панелей. Поскольку, согласно 6.7.б и табл. 27 [3], здание имеет жесткую конструктивную схему, направление ригелей может быть как поперечным, так и продольным. Принимаем поперечное направление ригелей.
Если типовые плиты (шириной 1,5 и 1,8 м) не укладываются в целое число по длине ригеля, то в условиях курсового проекта является допустимым изменение их ширины. Учитывая назначение здания (промышленное) и размер полнотелой нагрузки (2400 кг/м 2 ) на перекрытия, используются железобетонные ребристые плиты с ребрами вниз. Для возможности приведения сосредоточенных (от ребер) нагрузок от веса плит к равномерно распределённым по длине ригеля, их ширину следует принимать такой, что бы укладывалось в каждом пролёте не менее четырёх плит.
Предварительные размеры поперечного сечения элементов и расчетные сопротивления материалов
Размеры сечения определяются расчетом. Однако сначала для определения нагрузки от собственного веса элементов и значений расчетных пролетов необходимо предварительно задаться как размерами поперечного сечения балок (ригелей), так и глубиной их опирания на стену.
Рекомендуемые размеры сечения ригеля: высота h = (0,07…0.1)l1 = (0,07…0,1)5800 = 406…580. Ширина b = (0,3…0,5)h = (0,3…0,5)580 = 174…270. При этом высота принимается кратной 50 при h = 600 мм, h 600 мм, а ширина с округлением до размеров 150, 180, 200, 220, 250 мм и далее кратной 50 мм. Исходя из этих условий, принимаем h = 500 и b = 250.
Глубина опирания ригеля на стену и консоли колонны принимается 300 мм (по рисунку 2.б. МУ). Колонну принимаем квадратного сечения со стороной 300 мм.
Согласно 5.2.3. [1], для определения расчетных сопротивлений бетона Rb и Rbt необходимо установить значение коэффициента условий работы бетона γb1, учитывающего влияние характера (длительность действия) нагрузки и условий окружающей среды (влажность). В соответствии с 5.1.10.а [2] при продолжительном (длительном) действии нагрузки коэффициент γb1 = 0,9. При этом значение γb1 бетону В20 соответствует (с округлением) Rb = 13 МПа и Rbt = 0,95 МПа (прил. 2 МУ).
Согласно 5.2.6 и табл. 5. 8. [2] (см. так же прил. 3 МУ), продольной арматуре класса А400 соответствуют расчетные значения сопротивления растяжению и сжатию продольной арматуры Rs = Rsc = 355 МПа, растяжению поперечной арматуры – Rsw = 285 МПа. В соответствии с 5.2.1. [2] модуль упругости арматурной стали принимается одинаковым при растяжении и сжатии и составляет Es = 200 000 МПа.
Расчет неразрезного ригеля
Статический расчет
Ригель является элементом рамы, однако при свободном опирании его концов на наружные стены и равных пролетах его рассчитывают как неразрезную балку (11.2.3 [7]). C этих позиций рассматриваемый ригель представляет собой 4-х пролётную неразрезную балку (рис. 2 а, МУ).
Расчетные значения длины крайних l01 и промежуточных l02 пролетов отличаются от номинальных (расстояния между буквенными разбивочными осями, т.е. шага колонн в поперечном направлении l1), что обусловлено характером опирания ригелей на стены и колонны. Определяем численные значения расчетных пролетов: l01 = 5800 – 0,5 * 1000 – 200 + 150= 5250 мм;
l02 =5800–1000 = 4800 мм.
Расчетные значения постоянных и временных нагрузок определяются по их нормативным значениям умножением последних на коэффициенты надежности и ответственности γn и по нагрузке γf . Согласно п.2 прил. 7 [4] для здания II уровня ответственности γn = 1. Согласно 2.2 [4], для веса строительных конструкций: γf = 1,1 – для железобетонных плит и ригеля; γf = 1,3 для пола (со средней плотностью бетона 1600 кг/м 3 ).
Нагрузка от ребристых плит (при их количестве в пролете не менее 4) считается равномерно распределенной по длине ригеля.
Интенсивность равномерно распределенных нагрузок на ригель определяется по грузовой площади, с которой они передаются на 1м длины ригеля (т.н. погонный метр), равной 1м×l2 (рис. 1, МУ). Подсчет приведен в таблице 1, в которой для удобства не указаны постоянные множители к нормативным значениям всех видов нагрузки γn = 1 и l2 = 6 м.
Вычисление нагрузки на 1 пог. м ригеля
| Нагрузка | Нормативное значение нагрузки, кН | γf | Расчетная нагрузка на 1 пог.м ригеля, кН/м | |
| на 1м 2 площади | На 1 пог. М ригеля | |||
| 1. Постоянная 1.1 Вес пола толщиной t = 30 мм при средней плотности бетона ρ=16 кН/м 3 | 0,48 | 2,88 | 1,3 | 3,74 |
| 1.2 Вес ж/б плит перекрытия с ребрами вниз | 1,31 | 7,86 | 1,1 | 8,65 |
| 1.3 Собственный вес ж/б ригеля при h=0,50м; b=0,25м; ρ=25 кН/м 3 | — | 3,125 | 1,1 | 3,44 |
| Итого постоянная g | — | 13,87 | — | 15,83 |
| 2. Временная p | 1,2 | 172,8 | ||
| 3. Полная q = g + p | — | 157,87 | — | 188,63 |
Уточнение размеров поперечного сечения
Осуществляется из условия прочности нормальных сечений изгибаемых элементов при оптимальном для балок значении относительной высоты сжатой зоны ξ=x/h0=0,4 (сжатую продольную арматуру здесь не учитываем) и, согласно 6.2.33 [2], условия (6.65) прочности бетонной полосы между наклонными сечениями.
Определяем максимальные значения положительного изгибающего момента в 1-м пролете и поперечной силы слева от опоры В от полной расчетной нагрузки q = 188,63 кН/м.
Мl,max = 
QB,лев = 
Значению ξ = 0,4 соответствует αm= 0,32 (получено из таблицы прил. 4 МУ). Руководствуясь рис 2.г МУ, определяем рабочую высоту сечения из 1-го условия по формуле:

Теперь определяем рабочую высоту сечения из условия, где коэффициент φb1 = 0,3 (для простоты значения поперечной силы принимаем непосредственно у опоры В):

Задаемся диаметром стержня d=32 мм. Тогда толщина защитного слоя бетона аb=35 мм. Она должна составлять не менее диаметра стержня и не менее 20 мм. Кроме того, должна быть кратна 5 мм в целях стандартизации фиксаторов положения. Расстояние между осями продольных стержней, расположенных в 2 ряда по высоте сечения балки V1 = 70 мм. (прил.6 МУ)
Величина a=ab+0,5d+0,5V1=35+0,5∙32+0,5∙70=8,6 см. Тогда высота сечения h=h0+a=67,4+8,6=76см. Принимаем h=80см. Отношение ширины сечения к его высоте b/h=25/80=0,31 удовлетворяет рекомендуемое (0,3…0,5).
В связи с тем, что уточненные размеры сечения балки больше предварительно принятых (h=50 см, b=25 см), собственный вес балки увеличивается, что приводит к увеличению постоянной и полной нагрузок, расчетные значения которых на 1 метр ригеля составляют g = 17,89 кН и q =190,69 кН. Им соответствуют значения МI,max = 478,29 кНм и QВ,лев =600,67 кН. По этим усилиям, пользуясь формулами (1) и (2), снова определяем рабочую высоту сечения при b = 25 см и получим соответственно hо = 67,82 cм и hо = 61,61 см. Окончательно принимаем во всех пролетах h = 80 cм и b = 25 см.
Теперь, пользуясь тем же рисунком прил. 5, вычисляем положительные (в точках 1,2,3,4,6,7,8,9 и максимальных в 1-м и 2-м пролетах) и отрицательные (в точках 5,6,7,8,9 и 10) изгибающие моменты и максимальные поперечные силы на опорах А, В и С по формулам:


α = 0,6 – на опоре В слева.
α = 0,5 – на опоре В справа, на опоре С слева и справа.
Отрицательные моменты (в точках 5,6,7,8,9 и 10) вычисляются по тому же приложению, но при этом коэффициент 

В результате вычислений получены следующие значения изгибающих моментов и поперечных сил от действия уточненной полной расчетной нагрузки на ригель.
Положительные изгибающие моменты, кНм:
М1= 0,065∙190,69 ∙(5,25) 2 =341,6 кНм
М2= 0,09∙190,69 ∙(5,25) 2 =473 кНм
М3= 0,075∙190,69 ∙(5,25) 2 = 394,2 кНм
М4= 0,020∙190,69 ∙(5,25) 2 =105,1 кНм
МIImax=0,0625∙190,69∙(4,8) 2 = 274,6 кНм
Отрицательные изгибающие моменты, кНм:
Поперечные силы, кН
QА = 0,4∙190,69 ∙5,25= 400,4 кН
QВ,лев = 0,6∙190,69 ∙5,25= 600,7 кН
Соединив соответствующие ординаты в указанных точках, получим огибающую эпюру изгибающих моментов.
Типы поперечных сечений
Поперечные сечения стоек имеют различную форму. Она зависит от значения усилия, наличия эксцентриситета, длины стойки, конструкции опорных закреплений, общей компоновки объекта. Сжатые элементы должны быть не только прочны, но и устойчивы. Поэтому поперечные сечения сжатых элементов должны обладать возможно большей жесткостью по всем направлениям.
Во избежание местной потери устойчивости стенку стойки подкрепляют продольными ребрами жесткости. Последние ставятся* если
hCT lsCT > 40 уг210/(0,9зт) + 0,4А (19.4)
для двутаврового сечения и
hCT lsCT > 40 К210/(0,9зт) — f 0,2А (19.4′)
для коробчатого сечения. В формулах (19.4) и (19.4′): X — гибкость стойки; На — высота стенки; sCT — толщина стенки. Для сталей классов С 38/23—С 52/40 отношение половины ширины полки
двутавра к ее толщине не должно превосходить 16—14 при гиб
кости //>=50 и 20,5—18,5 при гибкости //г= 100.
Часто напряжения в сжатых элементах проверяют по преобразованной формуле
При этом произведение Ftp называют приведенной площадью сжатого элемента. Трудность подбора сечения сжатого
320*10 тіп И Коэффициент ф2, СООТ — ветствующий значению Яшах. ОпрЄДЄ — ляют напряжение в спроектированном сечении о — N/ (^фг), которое должно быть близким к [а]р. Допустимы отклонения а от Мр в пределах ±5%. В противном случае размеры поперечных сечений элементов изменяют в требуемом направлении. Обычно на второй или третьей стадии подбора сечения результаты оказываются удовлетворительными.
Пример расчета (рис. 19.3). Требуется подобрать поперечное сечение стойки; ее длина 1 = 8 м, продольная сжимающая сила Р=—940 кН; концы стойки закреплены шарнирно; материал — сталь класса С46/33 ([ 150 т]^1.
Значения коэффициентов фм в зависимости от тц и к для стали С 38/23 приведены в табл. 19.2.
При применении сталей других классов можно пользоваться «табл. 19.2, подставляя вместо гибкости элемента X значения условной гибкости:
где сгт — предел текучести стали. При этом значения фм не должны быть больше значений ф, приведенных в табл. 19.1.
В-третьих, следует проверить устойчивость от силы N в плоскости наибольшей гибкости, как правило, перпендикулярной плоскости действия момента М, с учетом изгибно-крутильной формы потери устойчивости. В этом случае проверка производится по формуле
Размер поперечного сечения это
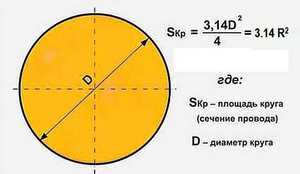
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
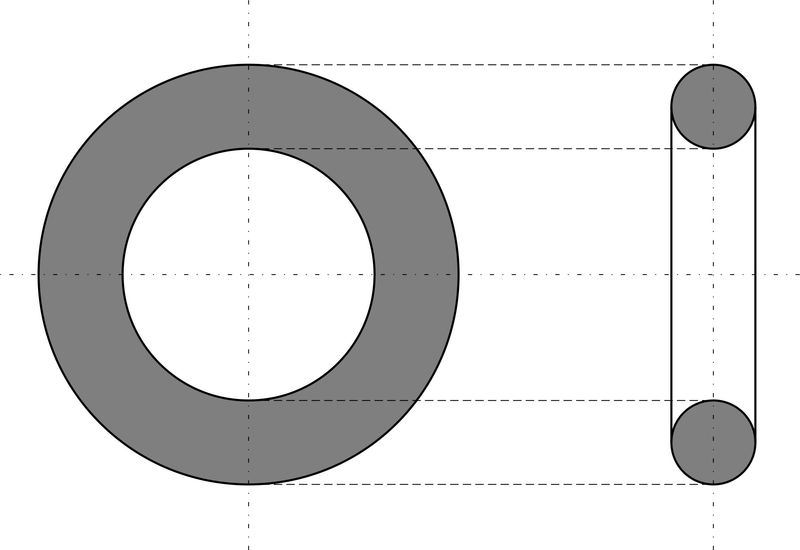
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
11.2.6 Минимальные размеры сечений следует назначать с учетом действующих усилий, требований технологического характера (защитный слой бетона, расположение арматуры, способ изготовления и т. д.), обеспечивающих надежность и долговечность конструкции, и с учетом экономических факторов.
11.2.7 Толщину железобетонных плит следует принимать не менее значений, указанных в таблице 11.3. Толщину железобетонных плит допускается снижать на 5 мм по сравнению с требуемыми по таблице 11.3 при их изготовлении в организациях, где действует сертифицированная система контроля качества.
11.2.8 Размеры сечений внецентренно сжатых элементов следует принимать такими, чтобы их гибкость l /i в любом направлении не превышала 200, а для колонн, являющихся элементами зданий, не превышала 120.
Таблица 11.3 — Минимально допустимая толщина железобетонных плит В миллиметрах
2 Перекрытия многоэтажных жилых и общественных зданий
3 Перекрытия многоэтажных производственных зданий
4 Плиты, работающие на сосредоточенную подвижную нагрузку
5 Для плит с сосредоточенным опиранием
Защитный слой бетона
11.2.9 Толщину защитного слоя бетона принимают из условий защиты арматуры от коррозии, воздействия огня и обеспечения ее совместной работы с бетоном.
11.2.10 Минимальное расстояние между поверхностью стержней продольной арматуры и ближайшей поверхностью бетона (защитный слой бетона) ограничивается величинами, указанными в таблице 11.4 с учетом класса по условиям эксплуатации.
11.2.11 Для сборных конструкций допускается снижать размер защитного слоя бетона на 5 мм по сравнению с указанными в таблице 11.4, но он не должен быть меньше 20 мм.
Таблица 11.4 — Минимально допустимая толщина защитного слоя бетона
Класс по условиям эксплуатации
ХD1, ХD2, ХD3, XF1, XF2, XF3, XF4
Минимальный размер защитного слоя, мм
11.2.12 Для фундаментов следует принимать толщину защитного слоя бетона не менее, мм:
а) при выполнении из монолитного железобетона:
— при отсутствии бетонной подготовки — 80;
— при наличии бетонной подготовки — 45;
б) при выполнении из сборного железобетона — 45.
11.2.13 Толщина защитного слоя бетона должна быть не менее:
— диаметра арматуры (если он не превышает 40 мм);
— максимального размера заполнителя (если он меньше 32 мм);
— максимального размера заполнителя плюс 5 мм (если он больше 32 мм).
11.2.14 Толщину защитного слоя бетона c поперечной и распределительной арматурой в конструкциях, работающих в условиях нормальной и слабоагрессивной сред, соответствующих классам Х0, ХС1, ХА1 (см. таблицу 5.2), следует принимать не менее 15 мм. При увеличении степени агрессивности среды на каждую ступень размер защитного слоя бетона дополнительно следует увеличивать на 5 мм.
Размещение арматуры в сечении
Расстояния между стержнями продольной арматуры
11.2.15 Расстояние в свету между стержнями продольной арматуры должно обеспечивать совместную работу бетона и арматуры, качественную укладку и уплотнение бетонной смеси и не должно быть менее значений, показанных на рисунке 11.1.
11.2.16 Наибольшие расстояния между осями стержней продольной арматуры, определяемые эффективностью работы бетонного сечения, усиленного арматурой, должны быть:
— в изгибаемых элементах — не более 400 мм, при этом площадь сечения конструктивно установленной арматуры должна быть не менее 0,15 % площади бетона bh (где h — расстояние между стержнями, b — половина ширины ребра элемента, но не более 200 мм);
— в линейных внецентренно сжатых элементах — не более 500 мм в плоскости изгиба и не более 400 мм в плоскости, перпендикулярной к плоскости изгиба.
Рисунок 11.1 — Минимально допустимые расстояния между продольными стержнями арматуры
в зависимости от положения конструкции при бетонировании
11.2.17 Количество стержней, доводимых до опоры, и максимально допустимые расстояния между ними должны быть:
в балках шириной менее 150 мм до опоры доводить не менее одного стержня;
в балках шириной более 150 мм до опоры доводить не менее двух стержней площадью сечения не менее 50 % расчетного сечения арматуры;
в плитах до опоры следует доводить стержни площадью сечения не менее 30 % сечения арматуры, подобранной из расчета на 1 м ширины сечения в зоне действия наибольшего изгибающего момента, выдерживая расстояние между стержнями не более 400 мм;
в неразрезных плитах, армированных рулонными сетками, все продольные стержни у промежуточных опор допускается переводить в верхнюю зону;
в неразрезных плитах расстояния между осями рабочих стержней в середине пролета и над опорами должны быть не более 200 мм — при толщине плиты до 150 мм и не более 1,5h — при толщине плиты более 150 мм.
Расстояние между стержнями поперечной арматуры
11.2.18 Поперечную арматуру следует устанавливать исходя из расчета на восприятие усилий, а также с целью фиксации в проектном положении и предотвращения бокового выпучивания в любом направлении продольных стержней.
11.2.19 Любая продольная арматура, установленная у поверхности железобетонной конструкции, должна охватываться поперечной арматурой, устанавливаемой с шагом не более 500 мм и не более удвоенной ширины грани элемента.
11.2.20 В плитах (высотой менее 300 мм) и балках (высотой менее 150 мм), при обеспечении прочности на поперечную силу, допускается поперечную арматуру не устанавливать.
11.2.21 В плитах (высотой более 300 мм) и балках (высотой более 150 мм) поперечная арматура устанавливается по расчету и по конструктивным соображениям с шагом:
а) на приопорных участках длиной 0,25l:
— при h 450 мм — не более 0,5h и 150 мм;
— при h > 450 мм — не более h/3 и 300 мм;
б) в средней части элемента независимо от высоты — не более 3/4h и 500 мм;
в) по всей длине элемента из условия обеспечения работы продольной арматуры, установленной по расчету в сжатой зоне сечения:
при fyd 400 Н/мм 2 — не более 500 мм и не более 15 и 20 в вязаных и сварных каркасах соответственно;
при fyd 450 Н/мм 2 — не более 400 мм и не более 12 и 15 в вязаных и сварных каркасах соответственно.
11.2.22 В элементах, работающих на изгиб с кручением, хомуты и поперечные стержни должны образовывать замкнутый контур.
11.2.23 В плитах, работающих на продавливание, поперечную арматуру следует устанавливать с шагом не более 1/3h и не более 200 мм на участке, расположенном между критическим периметром и наружным контуром площади смятия.
11.2.24 Во внецентренно сжатых линейных элементах поперечная арматура должна ставиться с шагом, не более:
на участках стыковки без сварки продольной рабочей арматуры — 10;
если площадь сечения сжатой арматуры S2 по расчету более 1,5 % — 10 и не более 300 мм;
если все сечение сжато и общая площадь сечения арматуры S1 и S2 по расчету более 3 % — 10 и не более 300 мм.
Поперечное армирование коротких консолей колонн выполняется горизонтальными и наклонными (угол наклона 45) хомутами. Шаг хомутов должен быть не более 0,25h (где h — высота консоли), 12 (где — диаметр продольной растянутой арматуры консоли) и не более 150 мм.
11.2.25 Во внецентренно сжатых элементах с косвенным армированием в виде сеток или в виде ненапрягаемой спиральной или кольцевой арматуры должны быть приняты (из арматуры класса S240, S500 диаметром не более 14 мм):
размеры ячеек сеток — не менее 45 мм, не более 100 мм и не более 1/4 размера меньшей стороны сечения;
шаг сеток — не менее 60 мм, не более 150 мм и не более 1/3 размера меньшей стороны сечения;
диаметр навивки спиралей или диаметр колец — не менее 200 мм;
шаг навивки спиралей или шаг колец — не менее 40 мм, не более 100 мм и не более 1/5 диаметра бетонного сечения, ограниченного спиралью или кольцом.
При усилении торцов внецентренно сжатых элементов следует устанавливать не менее четырех сеток на длине 15 (если продольная арматура гладкая), 10 (если продольная арматура имеет периодический профиль), считая от торца конструкции.
11.2.26 Конструктивное решение поперечной арматуры (хомуты, поперечные стержни, шпильки и т. д.) во внецентренно сжатых элементах должно обеспечивать крепление стержней продольной арматуры (перегиб или сварка в вязаных или сварных каркасах соответственно) на расстоянии не более 400 мм по ширине грани сечения с шагом не более 500 мм по длине элемента.