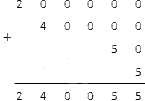Разрядные слагаемые что это такое 3 класс примеры
Разрядные слагаемые в математике
Число — это математическое понятие для количественного описания чего-либо или его части, служит также для сравнения целого и частей, расположения по порядку. Понятие числа изображается знаками или цифрами в различном сочетании. В настоящее время почти везде используются цифры от 1 до 9 и 0. Цифры в виде семи латинских букв применения почти не имеют и рассматриваться здесь не будут.
[block >
Натуральные числа
При счёте: «один, два, три… сорок четыре» или расстановке по очереди: «первый, второй, третий… сорок четвёртый» используются естественные числа, которые называются натуральными. Вся эта совокупность называется «ряд натуральных чисел» и обозначается латинской буквой N и не имеет конца, ведь всегда есть число ещё больше, и са́мого большого просто не существует.
Разряды и классы чисел
Разряды
Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.
Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.
Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.
Классы
Первый — единиц, содержит до 3 знаков:
Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.
Сорок пять состоит из четырёх десятков и пяти простых единиц.
[block > Второй — тысяч, от 4 до 6 знаков:
Эта сумма состоит из следующих разрядных слагаемых:
Здесь отсутствуют слагаемые выше четвёртого разряда.
Третий — миллионов, от 7 до 9 цифр:
Это число содержит девять разрядных слагаемых:
В этом числе нет слагаемых выше 7 разряда.
[block > Четвёртый — миллиардов, от 10 до 12 цифр:
Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.
Разрядные слагаемые 4 класса читаются слева направо:
Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.
[block > При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:
Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого́ третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.
Пятый — триллионов, от 13 до 15 знаков.
Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.
Шестой — квадриллионов, 16—18 цифр.
Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.
Седьмой — квинтиллионов, 19—21 знак.
Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.
Восьмой — секстиллионов, 22—24 цифры.
Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.
Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.
Сумма разрядных слагаемых натурального числа
Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.
В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.
Каким образом можно разложить число по разрядам?
Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах.
Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.
Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.
Сумма разрядных слагаемых натурального числа равна этому числу.
Перейдем к понятию разрядных слагаемых.
Разрядные слагаемые– это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.
Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы. Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.
Как раскладывать числа?
Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.
Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.
Как найти натуральное число, если известна сумма разрядных слагаемых?
Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.
Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.
Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.
Получаем: 
Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.
Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.
Разрядные слагаемые числа
Сумма разрядных слагаемых
Любое натуральное число можно записать в виде суммы разрядных слагаемых.
Как это делается, видно из следующего примера: число 999 состоит из 9 сотен, 9 десятков и 9 единиц, поэтому:
999 = 9 сотен + 9 десятков + 9 единиц = 900 + 90 + 9.
Числа 900, 90 и 9 — разрядные слагаемые. Разрядное слагаемое — это количество единиц в данном разряде.
Сумму разрядных слагаемых также можно записать следующим образом:
999 = 9 · 100 + 9 · 10 + 9 · 1.
Числа, на которые выполняется умножение (1, 10, 100, 1000 и т. д.), называются разрядными единицами. Так, 1 — это единица разряда единиц, 10 — единица разряда десятков, 100 — единица разряда сотен и т. д. Числа, которые умножаются на разрядные единицы выражают количество разрядных единиц.
Запись любого числа в виде:
12 = 1 · 10 + 2 · 1 или 12 = 10 + 2
называется разложением числа на разрядные слагаемые (или суммой разрядных слагаемых).
Сумма разрядных слагаемых — это запись многозначного числа в виде сложения количеств его разрядных единиц.
Пример 1. Запишите числа в виде суммы разрядных слагаемых: 3278, 5031, 3700.
1) 3278 = 3 · 1000 + 2 · 100 + 7 · 10 + 8 · 1 = 3000 + 200 + 70 + 8;
2) 5031 = 5 · 1000 + 0 · 100 + 3 · 10 + 1 · 1 = 5000 + 30 + 1;
3) 3700 = 3 · 1000 + 7 · 100 + 0 · 10 + 0 · 1 = 3000 + 700.
Обратите внимание, что разрядные единицы могут быть записаны в виде степени числа 10:
1) 3278 = 3 · 10 3 + 2 · 10 2 + 7 · 10 1 + 8 · 1;
2) 5031 = 5 · 10 3 + 0 · 10 2 + 3 · 10 1 + 1 · 1 = 5 · 10 3 + 3 · 10 1 + 1;
Пример 2. Записать число, представленное в виде суммы разрядных слагаемых:
а) 3 · 10 2 + 2 · 10 + 7 = 300 + 20 + 7 = 327;
б) 5 · 10 3 + 0 · 10 2 + 4 · 10 + 1 = 5000 + 40 + 1 = 5041;
в) 8 · 10 2 + 0 · 10 + 5 = 800 + 5 = 805;
г) 1 · 10 3 + 6 · 10 2 + 7 · 10 = 1000 + 600 + 70 = 1670.
Калькулятор разложения числа на разрядные слагаемые
Математика. 3 класс
Конспект урока
Математика, 3 класс.
Урок № 53. Замена числа суммой разрядных слагаемых.
Сложение (вычитание) трёхзначных чисел
Перечень вопросов, рассматриваемых в теме:
— Как заменить трёхзначное число суммой разрядных слагаемых?
— Как упорядочивать заданные числа?
ЧИСЛА – это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т. д.).
Позиция (место) цифры в записи числа называется РАЗРЯДОМ.
Каждые три разряда натуральных чисел образуют КЛАСС.
Основная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. с. 48-49.
2. Волкова С. И. Математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018. с. 62-71.
3. Волкова С. И. Математика. Тесты. 3 кл. — М.: Просвещение, 2018. с. 38-45.
Теоретический материал для самостоятельного изучения
Как вы думаете, какова связь между этими изображениями?
Каждый ребёнок с раннего возраста умеет разбирать и собирать матрёшку. А как же этот фокус (секрет) применить к многозначным числам?
Если вы будете внимательным, то к концу урока вы научитесь раскладывать и складывать многозначные числа так же легко как матрёшку.
Вспомним, как образуются трёхзначные числа.
На первом месте стоят сотни, на втором – десятки и на третьем – единицы.
Единицы, десятки и сотни это разряды первого класса – класса единиц.
Попробуйте прочитать числа из таблицы.
Помните: читаем слева направо.
Четыреста пятьдесят шесть, шестьсот, пятьдесят, четыре.
А теперь вспомним матрёшку.
Представьте себе, что большая матрёшка это самый большой разряд. У нас это – сотни, мы не увидим следующую, пока не откроем большую и так далее. Теперь легко запомнить, что при записи разрядов на первом месте самый большой разряд.
Но может случиться так, что большой матрёшки не будет, сотен нет.
Мы же её не видим, значит и на месте этого разряда в записи числа ничего не будет.
Так было с числом 50 из таблицы.
Ноль впереди не пишется!
Как же представить многозначное число в виде суммы разрядных слагаемых?
Расставить матрёшек по порядку! (по росту)
Посмотрим, как это работает с числами.
Число шестьсот тридцать один. Все три матрёшки (разряда) на месте.
6 – сотни, 3 – десятки, 1 – единицы. Значит, в сумме разрядных слагаемых будут представлены все три разряда.
Итак, шестьсот тридцать один это сумма чисел шестьсот, тридцать и один
Каждое разрядное слагаемое показывает количество единиц в этом разряде
6 сотен – 600, 1 сотня – 100, 5 сотен – 500.
8 десятков – 80, 1 десяток – 10.
Единицы не меняются.
Итак, чтобы правильно записать число в виде суммы разрядных слагаемых, надо хорошо знать разряды.
Рассмотрим несколько примеров.
В числе 309 на месте десятков – 0 (нет одной матрёшки) поэтому в сумме разрядных слагаемых мы этот разряд пропускаем. Получается 309 это 300 и 9.
В числе 970 отсутствуют единицы в разряде единиц (нет последней матрёшки). Значит, в сумме этот разряд не обозначаем.
222 – все разряды на месте. Выстраиваем матрёшек по росту. 200 + 20 + 2
Это умение необходимо при сравнении, сложении и вычитании многозначных чисел.
Задания тренировочного модуля:
3. Укажите ряд чисел, расположенных в порядке убывания
Что такое разрядные слогаемые
Ответ или решение 2
Определим, что такое разрядные слагаемые
Разрядные слагаемые – это сумма чисел с разной разрядностью.
Возьмем на примере, число 86. Разложим данное число на десятки и единицы. Получаем: 86 = 80 + 6 = 8 * 10 + 6 * 1. Отсюда видим, что число 86 состоит из 8 десятков и 6 единиц. Это и есть разрядные слагаемые.
Числа 1, 10, 100, 1000 и так далее – это разрядные единицы.
Запишем разделение разрядных слагаемых:
Любое натуральное число можно разделить на разрядные слагаемые и записать в виде суммы.
Примеры разрядных слагаемых:
Рассмотрим пример определения разрядных слагаемых числа 92586
Сначала, разложим число 92586 на разрядные слагаемые и получим:
92 586 = 90000 + 2000 + 500 + 80 + 6 = 9 * 10 000 + 2 * 1 000 + 5 * 100 + 8 * 10 + 6 * 1.
Запишем, из чего состоит число 92 586:
Сделаем вывод, что любое число можно разделить на разрядные слагаемые. Разрядные слагаемые помогают при решении более сложных примеров и задач.
Разрядное слагаемое — это любое натуральное многозначное число, которое можно представить в виде суммы разрядных слагаемых. Разложить число на разрядные слагаемые значит разделить число на разряды: единицы, десятки, сотни, тысячи, десятки тысяч и так далее.
Примеры разложения чисел на разрядные слагаемые:
Более сложный пример с большим числом разрядов: