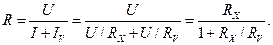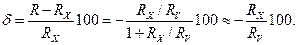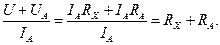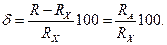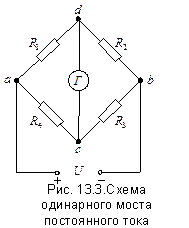зачем в косвенном методе вольтметра амперметра проводится три измерения с усреднением результата

Измерение средних сопротивлений косвенным методом (амперметра-вольтметра).

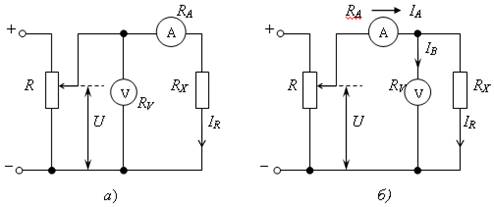
Измеряемое сопротивление R_X включается в цепь последовательно с амперметром. Вольтметр подключается в зависимости от величины измеряемого сопротивления либо перед амперметром (рис. а), либо после амперметра (рис. б). Сопротивление R_X определяется приближенно по формуле, вытекающей из закона Ома, подставив в нее значения тока и напряжения, измеренные приборами

При подключении вольтметра за амперметром (рис. а), то амперметр будет измерять сумму тока, проходящего через измеряемое сопротивление, и тока, проходящего через вольтметр. При этом сопротивление R_X определяют по формуле:

Такую схему применяют, если внутренне сопротивление вольтметра R_V значительно превышает значение измеряемого сопротивления (в 100 и более раз).

При подключении вольтметра перед амперметром (рис. б) он покажет сумму напряжений на амперметре и на измеряемом сопротивлении. При этом измеряемое сопротивление определяют по формуле:

Такую схему применяют, если сопротивление амперметра составляет менее 1% от измеряемого сопротивления.

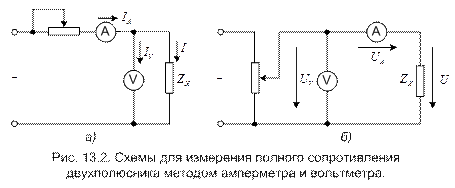
Рис. Измерение средних сопротивлений косвенным методом.

Источник

Косвенные (приближенные) методы измерения с помощью вольтметра – амперметра представляют собой измерение тока и напряжения в цепи с измеряемым двухполюсником и последующим расчетом по закону Ома его параметров, а именно: активного и полного сопротивления, индуктивности и емкости.

Измерение активного сопротивления производится на постоянном токе, при этом включение резистора R_х в измерительную цепь возможно по схемам, представленным на рис. 14.1, а и рис. 14.1, б.

Рис. 14.1. Измерение активных больших (а) и малых (б) сопротивлений R_X методом вольтметра- амперметра

Измерение модуля полного (комплексного) сопротивления Z _X выполняется на переменном токе с частотой f по схемам, представленным на рис. 14.2.

По показаниям вольтметра и амперметра определяют модуль полного сопротивления

,

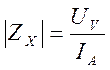
Анализ методических погрешностей измерения модуля полного сопротивления вольтметром – амперметром приводит к результату, что схему на рис. 14.1, а целесообразно применять при Z_X >> Z_V, а схему на рис. 14.1, б – при Z_X > Z_V (а) и при Z_X > С_Х, то формулу (14.5) можно упростить

.

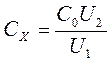
Измерение индуктивности катушки методом вольтметра – амперметра возможно с помощью схем, изображенных на рис. 14.5, если ее сопротивление R_L значительно меньше реактивного сопротивления Х_L.

Из рис. 14.5 следует

, откуда по показаниям вольтметра и амперметра получим искомое измеренное значение индуктивности

.

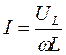
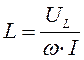
Рис. 14.5. Измерение больших (а) и малых (б) индуктивностей методом вольтметра- амперметра

Для более точного определения индуктивности следует учесть сопротивление катушки R_L по формуле

.

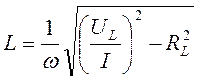
Погрешности измерения параметров элементов электрорадиоцепей методом вольтметра – амперметра на низких частотах составляют 0,5 – 10% и увеличиваются с ростом частоты.

14.2. Прямые методы измерения параметров электрорадиоцепей.

Кило-омметры и мега-омметры

Прямые методы измерения параметров электрорадиоцепей реализуются в приборах для измерения сопротивления постоянному току. Этими приборами являются омметры электромеханического или электронного типа.

Электромеханические омметры строятся на основе приборов магнитоэлектрической системы и в зависимости от величины измеряемого сопротивления подразделяются на кило- омметры и мега- омметры. В кило- омметрах измерительная обмотка прибора включена последовательно (рис. 14.6, а), а в мага- омметрах (рис. 14.6, б) – параллельно измеряемому сопротивлению R_X.

Источник

Измерение электрического сопротивления постоянному току

Метод амперметра-вольтметра

Пожалуй, он самый простой для измерения средних и малых сопротивлений R.

При измерении малых R рекомендуют применять такую схему:

Потому что в данном случае I_A≈I_R из-за большого внутреннего сопротивления вольтметра относительно R и будет выполнено равенство I_V«I_R. При среднем значении R рекомендована такая схема:

Из-за наличия внутренних сопротивлений в приборах возникает погрешность, что есть основным недостатком этого метода. Но при измерении малых R сопротивление вольтметра будет равно R_V>100R, а для измерения средних R амперметра R_A 9 Ома применяют специальные электронные устройства, которые носят название тераомметров.

Мостовой метод

Устройства, применяемые для реализации такого измерения, именуют измерительными мостами. Четырехплечевой или одинарный мост содержит в себе две диагонали и четыре плеча:

Мост образуют три резистора, значения которых известны – R₂, R₃, R₄ и соответственно сопротивление, значение которого необходимо измерить R_x. В одну из диагоналей моста необходимо подключить источник питания, для данного случая источник Е₀ подключенный к зажимам a и b, а другую нулевой индикатор НИ (зажимы c и d), который выполняет роль указателя симметричности моста. Когда потенциалы в точках c и d будут равны, то отклонение в НИ протекает ток I_НИ = 0 и его отклонение тоже равно нулю. Мост в состоянии равновесия. Будут выполнятся следующие соотношения: I₁ = I₂, I₃ = I₄, R_xI₁=R₃I₃, R₂I₂=R₄I₄. Учтя равенство токов и почленно разделив два последних уравнения получим:

Из данного выражения можем выделить искомое сопротивление:

Плечо R₂ именуют плечом сравнения, а плечами отношений R₃ и R₄ соответственно.

Методом одинарного моста измеряют только средние сопротивления. Измерять им малые и большие сопротивления не рекомендуют. Нижний предел измерений моста (единицы Ом) ограничивается влиянием сопротивлений проводов и контактов, которые подключаются в плечо ас последовательно с объектом измерения R_х. Верхний предел (10 5 Ом) ограничен шунтирующим действием токов утечки.

Компенсационный метод

Его применяют для получения повышенной точности измерения. Ниже показана схема подобной установки:

В данную схему входит компенсатор постоянного тока, двухпозиционный переключатель (П2 и П1), резистор образцовый R₀, а также источник питания Е и измеряемый резистор R_х. Измеряв падение напряжения на каждом из резисторов при двух разных положениях переключателя определяют – U_R0=R₀I и U_RХ=R_ХI. Из этих выражений можно получить следующую формулу:

При выполнении измерений необходимо ток I поддерживать постоянным и не допускать изменения его значения, для обеспечения точности измерения.

Источник

Метод амперметра – вольтметра

Измерение параметров элементов электрических цепей

Электрические цепи представляют собой совокупность соединенных друг с другом элементов – источников электрической энергии и нагрузок в виде резисторов, катушек индуктивности, конденсаторов. При определенных допущениях эти нагрузки можно рассматривать как линейные пассивные двухполюсники с сосредоточенными постоянными, характеризуемые некими идеальными параметрами – сопротивлением R, индуктивностью L, емкостью С.

При измерении, однако, не всегда удается определить значение того или иного параметра, соответствующее идеальному, совершенному виду элемента. Несовершенство конструкции и характеристик применяемых материалов является причиной появления так называемых остаточных (паразитных) параметров элементов. Так, наряду с главным параметром катушки индуктивности – индуктивностью, она обладает собственной емкостью и активным сопротивлением; резистор, обладая активным сопротивлением, имеет также определенную индуктивность т.п.

С учетом остаточных параметров конденсатор, катушку индуктивности или резистор можно характеризовать некоторым эффективным значением емкости, индуктивности, сопротивления, которые зависят от частоты. Поэтому эффективные параметры компонентов необходимо измерять на рабочих частотах, если их влиянием на результат измерения нельзя пренебречь.

В зависимости от объекта измерений, требуемой точности результата, диапазона рабочих частот и других условий для измерения параметров двухполюсников применяют различные методы и средства измерений. Наиболее распространенными являются следующие методы измерения: амперметра – вольтметра, непосредственной оценки, мостовой, резонансный и дискретного счета.

Метод амперметра – вольтметра

Измерение методом амперметра – вольтметра сводится к измерению тока и напряжения в цепи с измеряемым двухполюсником и последующему расчету его параметров по закону Ома. Метод может быть использован для измерения активного и полного сопротивления, индуктивности и емкости.

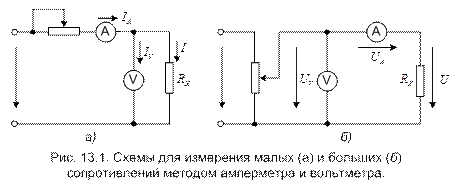
Измерение активных сопротивлений производится на постоянном токе, при этом включение резистора R_Х в измерительную цепь возможно по схемам, представленным на рис. 13.1, а и б.

В схеме рис. 13.1,а вольтметр показывает значение напряжения на зажимах R_Х, а амперметр — сумму токов I_V+I.

Следовательно, результат измерения R, вы­численный по показаниям приборов, будет отличаться от R_Х :

Относительная погрешность измерения в процентах

Здесь приближенное равенство справедливо, так как при правильной организации эксперимента предполагается выполнение условия R_V >>R_Х.

Относительная погрешность измерения в процентах в данном случае равна:

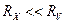
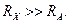
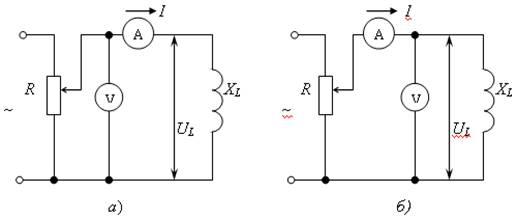
Сравнивая полученные выражения относительных по­грешностей, приходим к выводу: в схеме рис. 13.1,а на методическую погрешность результата измерения оказы­вает влияние только сопротивление R_V ; для снижения этой погрешности необходимо обеспечить условие ; в схеме рис. 13.1,б на методическую погрешность результата измерения оказывает влияние только R_A; снижение этой погрешности достигается выполнением условия Таким образом, при практическом ис­пользовании данного метода можно рекомендовать пра­вило: измерение малых сопротивлений следует произво­дить по схеме рис. 13.1,а; при измерении больших сопротивлений предпочтение следует отдавать схеме рис. 13.1, б.

Измерение полного сопротивления Z_X выполняется на переменном токе частотой f (рис. 13.2). По показаниям вольтметра и амперметра определяют модуль полного сопротивления

,

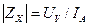
где 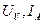— показания вольтметра и амперметра.

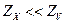
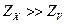
Выполнив аналогично предыдущему анализ методической погрешности, придем к выводу, что схему, представленную на рис. 13.2, а, целесообразно применять при , а на рис. 13.2, б – при .

Емкостное сопротивление конденсатора

,

.

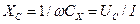
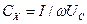
При измерении емкости этим методом необходимо знать частоту источника питания. Для измерения больших емкостей рекомендуется схема а), а для малых емкостей – схема б).

Измерение индуктивности катушки методом амперметра – вольтметра возможно, если ее сопротивление R_L значительно меньше реактивного сопротивления X_L. При этом

, откуда .

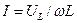
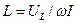
Если требуется получить более точный результат, то необходимо учесть сопротивление катушки. Так как

,

.

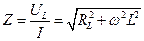
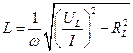
Погрешности измерения параметров элементов цепей методом амперметра – вольтметра на низких частотах составляют 0.5-10%. Погрешности измерения возрастают с увеличением частоты.

Мостовой метод

Важным классом средств измерения, предназначенных для измерения параметров элементов электрических цепей методом сравнения, являются мосты. Сравнение измеряемой величины (сопротивления, емкости. Индуктивности) с образцовой мерой при помощи моста в процессе измерения может осуществляться вручную или автоматически, на постоянном или на переменном токе. Мостовые схемы обладают большой точностью, высокой чувствительностью, широким диапазоном измеряемых значений параметров. На основе мостовых методов измерения строятся средства измерения, предназначенные как для измерения какой-либо одной величины, так и универсальные аналоговые и цифровые приборы.

Одинарный мост постоянного тока

Простейшая схема одинарного моста представлена на рис.13.3. Четыре резистора R₁,R₂,R₃,R₄ (их называют плечами моста) соединены в кольцевой замкнутый контур. Точки соединения сопротивлений называют вершинами моста.

Цепи, соединяющие противоположные вершины, называют диагоналями. Диагональ ab содержит источник питания и называется диагональю питания. Диагональ cd, в которую включен индикатор Г, называется измерительной диагональю. В мостах постоянного тока в качестве индикатора обычно используется гальванометр.

В общем случае зависимость протекающего через гальванометр тока I_г от сопротивления плеч, сопротивления гальванометра R_г и напряжения питания U имеет вид

. (13.1)

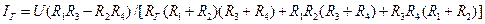
Измерение сопротивления может производиться в одном из двух режимов работы моста: уравновешенном либо неуравновешенном. Мост называется уравновешенным, если разность потенциалов между вершинами c и d равна нулю, а, следовательно, и ток через гальванометр равен нулю.

Из (13.1) следует, что I_г = 0 при

. (13.2)

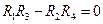
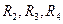
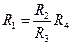
Это условие равновесия одинарного моста постоянного тока можно сформулировать следующим образом: для того, чтобы мост был уравновешен, произведения сопротивлений противолежащих плеч моста должны быть равны. Если сопротивление одного из плеч моста (например, R₁) неизвестно, то уравновесив мост путем подбора сопротивлений плеч , находим из условия равновесия

.

В реальных мостах постоянного тока для уравновешивания моста регулируются отношение 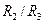и сопротивление плеча , которые, соответственно, называют плечами отношения и плечом сравнения.

В состоянии равновесия моста ток через гальванометр равен нулю и, следовательно, колебания напряжения питания и сопротивления гальванометра влияния на результат измерения не оказывают (важно лишь, чтобы чувствительность гальванометра была достаточной для надежной фиксации состояния равновесия). Поэтому основная погрешность уравновешенного моста определяется чувствительностью гальванометра, чувствительностью схемы, погрешностью сопротивлений плеч, а также сопротивлениями монтажных проводов и контактов.

Двойной мост постоянного тока. Схема двойного моста представлена на рис. 13.4 .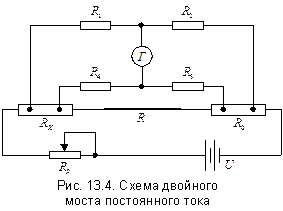

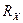
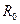
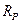
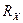
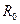
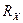
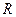
Для исключения влияния сопротивлений соединительных проводов и переходных сопротивлений контактов измеряемое сопротивление присоединяется по четырехзажимной схеме включения: двумя токовыми зажимами в цепь источника питания моста, а двумя потенциальными – в измерительную цепь. Аналогичные зажимы имеет образцовое сопротивление . В цепь источника питания моста входит регулировочное сопротивление , измеряемое сопротивление , образцовое сопротивление (одного порядка по величине с ) и малого сопротивления .

Сопротивления плеч R₁,R₂,R₃ и R₄, входящие в измерительную цепь, выбирают достаточно большими (сотни и тысячи Ом), поэтому влияние сопротивлений монтажных проводов и переходных сопротивлений в контактах пренебрежимо мало.

При равновесии моста формула для определения сопротивления имеет вид

. (13.3)

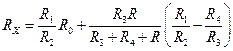
При соблюдении равенства

(13.4)

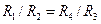
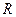
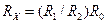
и достаточно малом сопротивлении вторым членом формулы (13.3) можно пренебречь. Тогда формула (13.3) упрощается до следующей

.

Равенство (13.4) должно соблюдаться постоянно, поэтому резисторы R₁,R₂ и R₃,R₄ регулируются при помощи спаренных органов управления. Резистор 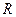представляет собой короткий отрезок медной шины большого сечения.

Промышленностью выпускаются одинарные и одинарно-двойные мосты постоянного тока классов точности от 0.005 до 5.

Измерительные мосты переменного тока

Для измерения емкости, индуктивности, взаимной индуктивности и тангенса угла потерь конденсаторов применяются мосты переменного тока, схемы которых отличаются большим разнообразием. Кроме простых четырехплечих мостовых схем существуют и более сложные мостовые схемы. Эти схемы путем последовательных эквивалентных преобразований могут быть приведены к простой четырехплечей схеме, которая является, таким образом, основной.

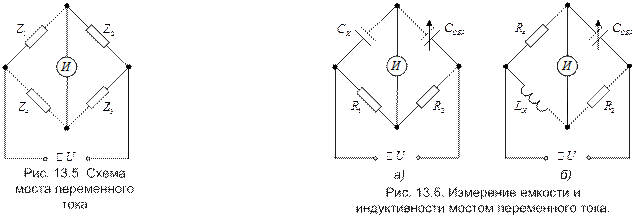
Схема одинарного четырехплечего моста переменного тока приведена на рис. 13.5. Так как мост питается напряжением переменного тока, то в качестве индикатора в нем применяются электронные милливольтметры переменного тока, либо осциллографические индикаторы нуля.

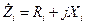
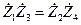
В общем случае сопротивления плеч моста переменного тока представляют собой комплексные сопротивления вида . Аналогично соотношению (13.2) условие равновесия одинарного моста переменного тока имеет вид:

.

Записав это выражение в показательной форме, получим

, (13.5)

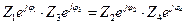
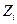
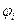
где — модуль комплексного сопротивления; — фазовый сдвиг между током и напряжением в соответствующем плече.

Соотношение (13.5) распадается на два скалярных условия равновесия:

(13.6)

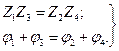
Отсюда следует, что в схеме моста переменного тока равновесие наступает только при равенстве произведений модулей комплексных сопротивлений противолежащих плеч и равенстве сумм их фазовых сдвигов. При этом нужно иметь в виду, что при изменении значений активных и реактивных составляющих одновременно изменяются и модуль, и фаза, поэтому мост переменного тока можно привести к состоянию равновесия лишь большим или меньшим числом переходов от регулирования одного параметра к регулированию другого.

Второе уравнение (13.6) показывает, какими по характеру должны быть сопротивления плеч мостовой схемы, чтобы обеспечить возможность ее уравновешивания. Так, например, если в двух смежных плечах включены активные сопротивления (φ = 0), то в двух других смежных плечах обязательно должны быть сопротивления одного характера – или индуктивности, или емкости.

Для измерения емкости конденсаторов без потерь используется мостовая схема, приведенная на рис. 13.6, а. Условие равновесия для этой схемы имеет вид

,

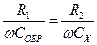
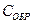
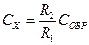
где — образцовый конденсатор переменной емкости, откуда

.

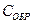
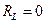
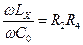
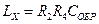
Мостовая схема для измерения индуктивности приведена на рис. 13.6, б. В качестве плеча сравнения здесь также используется конденсатор переменной емкости . Полагая, что активное сопротивление катушки пренебрежимо мало ( ), получим условие равновесия

,

.

Погрешность моста переменного тока определяется погрешностями элементов, образующих мост, переходных сопротивлений контактов, чувствительностью схемы и индикатора. Мосты переменного тока больше, чем мосты постоянного тока, подвержены влиянию помех и паразитных связей между плечами, плечами и землей, мостом и оператором. Именно поэтому, даже при тщательном экранировании моста и принятии других мер защиты, погрешности мостов переменного тока больше, чем погрешности мостов постоянного тока. Промышленностью выпускаются мосты переменного тока классов точности от 0.1 до 5.0.

Мосты переменного тока работают обычно на низких частотах 100 Гц и 1000 Гц. При работе на повышенных частотах погрешности измерения резко возрастают.

Источник