Как проверить что точка внутри треугольника

Как проверить что точка внутри треугольника

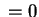
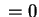
Решение. Точка лежит внутри треугольника, если она расположена правее прямой x, выше прямой y и ниже прямой x+y=2. Таким образом, принадлежность точки с координатами (x,y) нашему треугольнику определяется истинностью логического выражения

Поэтому наше решение будет содержать ровно один условный оператор:

module ПроверкаРасположенияТочки;
const НУЛЬ = 0;
var X,Y : Real;
begin
read(X,Y);
writeLn (‘Точка с координатами (‘,X, ‘, ‘, Y, ‘) ‘);
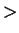
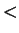
if (X > НУЛЬ) & (Y > НУЛЬ )& (X + Y НУЛЬ )&(Y $» BORDER=0 height=33 width=19 align=CENTER> НУЛЬ ) &(X+Y 2)) и (X = НУЛЬ) or (Y = НУЛЬ) or (X+Y $» BORDER=0 height=33 width=19 align=CENTER> = 2).

Поэтому печать ответа можно записать чуть короче:

module ПроверкаРасположенияТочки2;
const НУЛЬ = 0;
var X,Y : Real;
begin
read(X,Y);
writeln (‘Точка с координатами (‘,X, ‘, ‘, Y, ‘) ‘);
if (X = 2)
then write (‘ не ‘)
end;
writeln (‘ принадлежит треугольнику.’)
end ПроверкаРасположенияТочки2.

Источник

Русские Блоги

Как определить, находится ли точка внутри треугольника

Основная мысль

Как показано на рисунке, точка P находится внутри треугольника ABC, о чем можно судить по следующим трем условиям:

Если три вышеуказанных условия выполняются одновременно, точка P находится внутри треугольника ABC.

Затем математический инструмент перекрестного произведения будет использоваться, чтобы определить, на какой стороне линии находится точка.

Определите, на какой стороне линии находится точка

где, Угол вектора, Вектор, и с Все они вертикальны, а направление соответствует правилу правой спирали, как показано на рисунке ниже:

Следующая программа обработки может проверить правильность перекрестного произведения, используемого для определения, на какой стороне прямой находится точка:

Заинтересованные читатели также могут попробовать перекрестный метод.

Реализация алгоритма

Обратите внимание, что прочитать все сразу непросто, но легче понять, является ли это координатой Z после перекрестного умножения вектора AB и вектора AC.

Затем соответственно вычислите, какая сторона P находится на AB, CA, BC:

Наконец, определите, находятся ли они на одной стороне:

Это все алгоритмы! Наконец, зайдите в программу для проверки.

Источник

Определение принадлежности точки треугольнику

Дано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты.

Что нужно узнать: нужно установить принадлежность точки треугольнику.

В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику.

Метод сравнения площадей

В данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно.

Затем находится площадь самого треугольника ABC.

Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность.

Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий.

Простейшая реализация алгоритма:

Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить.

Метод относительности

Данный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.

На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику.

Всё относительно!

Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой.

Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику.

Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции!

Векторный метод

Третий метод который я освещаю для меня самый интересный.

Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма…

Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :]

1) одну вершину треугольника помещаем в координаты (0;0);

2) две стороны, выходящие из этой вершины, представляем как вектора.

Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)

Источник

Точка внутри треугольника

Решение некоторых задач требует иногда определить находится точка внутри треугольника или нет. Есть довольно много вариантов установления принадлежности точки треугольнику.

Способ сравнения площадей

Пусть нужно проверить находится ли точка D внутри треугольника АВС. Предположим, точка D внутри треугольника и является общей вершиной трех треугольников, которые она образовала с каждой из сторон треугольника АВС. Воспользовавшись формулой Герона, находим площади трех вновь образованных треугольников (DВС, DАВ, DАС). Сумму их площадей сравниваем с площадью первоначального тр-ка АВС. Равенство величин будет означать, что точка принадлежит треугольнику.

Способ геометрического луча

Из заданной точки в любом направлении выпускается луч. Нечетное число пересечений луча со сторонами треугольника означает, что точка расположена внутри треугольника.

Способ относительности

Этот вариант основан на утверждении, что все точки треугольника располагаются по одну сторону от прямой, прошедшей через каждую его сторону.
Выбираем ориентир движения по вершинам треугольника. Предположим, по часовой стрелке. Стороны треугольника принимаем за прямые. Пройдя по часовой стрелке все стороны, определяем, по какую сторону от прямой находится точка. Если для каждой из сторон точка лежит справа, она принадлежит треугольнику.
Если точка находится слева хоть одной из сторон, принятых за прямую, условие ее принадлежности треугольнику не выполняется.

Источник

Как проверить принадлежит ли точка треугольнику?

Как проверить, принадлежит ли точка треугольнику
Пожалуйста, помогите найти ошибку: Sub xy() Dim x1, y1, x2, y2, x3, y3 As Single x1 =.

Проверить, принадлежит ли точка M(x,y) треугольнику с заданными вершинами
помогите плиз две задачки решить: Проверить, принадлежит ли точка M(x,y) треугольнику с.

Проверить принадлежит ли точка плоскости с координатами (x,y) треугольнику с заданными вершинами
Даны два вещественных числа x,y. Если точка плоскости с координатами (x,y) принадлежит треугольнику.

Принадлежит ли точка треугольнику
дан три угольник ABC с координатами вершин A(xa,ya), B(xb,yb), C(xc,yc), Пользователь водит.

точка будет принадлежать треугольнику, если будет принадлежать одновременно трем полуплоскостям, пересечение которых и есть треугольник.

далее нужно найти уравнения прямых, которые содержат стороны треугольника, составить 3 неравенства, и решить систему из этих 3х неравенств.

Решение

Добавлено через 13 минут
вот ещо одно решения етой задачи

Любое вычисление более-менее извращенных функций, вроде синуса-косинуса, или квадратного корня, явно снизит скорость выполнения данного алгоритма. Тут без вопросов, и спорить не о чем. Остается только согласиться.

С другой стороны, задача-то простая. Не элементарная, но достаточно простая. Somebody уже показал, что все решается без особого выпендрежа. Ну, и нафиг оно, усложнение!

Решение

Господа. Должен заметить, что код первого решения вроде как неверен. Я не знаю, проверял ли ПроСтоСанек свое решение, но он в цикле явно «гадит» мимо массива (из-за ++i вместо i++)
Выкладываю код моего решения, которое проверено и работает (косметические изменения плюс исправленая ошибка, для тех, кто обожает копипасту с форумов =) ).

При обнаружении в программе цикла for первым выполняется инициализирующее_выражение, в котором обычно устанавливается счетчик цикла. Это происходит только один раз перед запуском цикла. Затем анализируется условное_выражение, которое также называется условием прекращения цикла. Пока оно равно true, цикл не прекращается.

Каждый раз после всех строк тела цикла выполняется модифицирующее_выражение, в котором происходит изменение счетчика цикла. Как только проверка условного_выражения даст результат false, все строки тела цикла и модифицирующее_выражение будут пропущены и управление будет передано первому выражению, следующему за телом цикла.

Источник