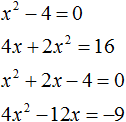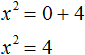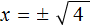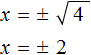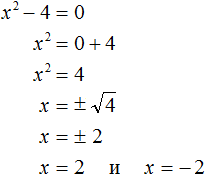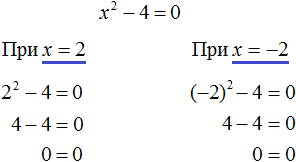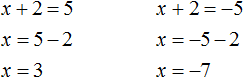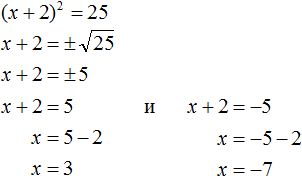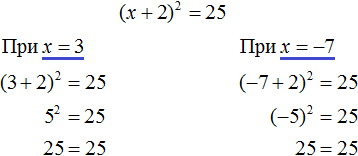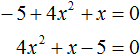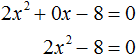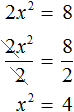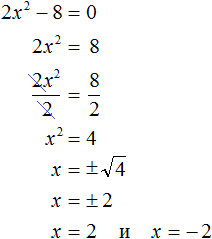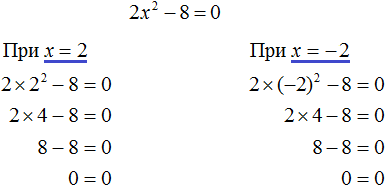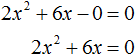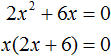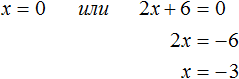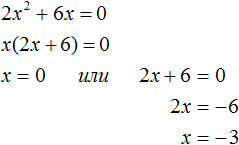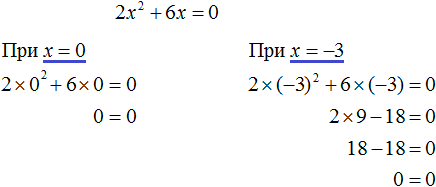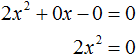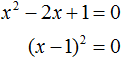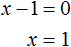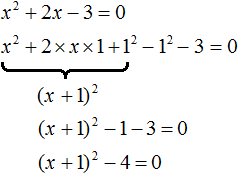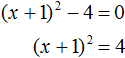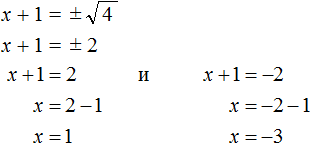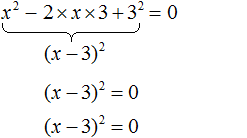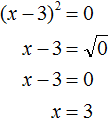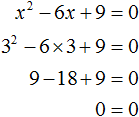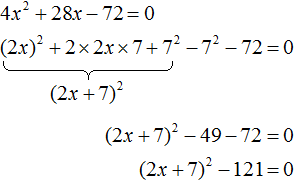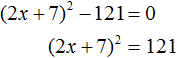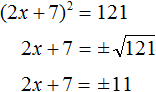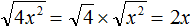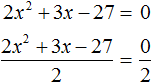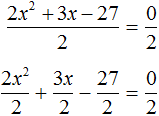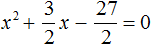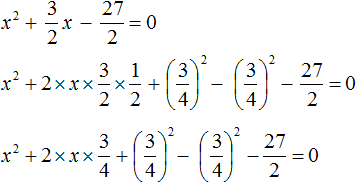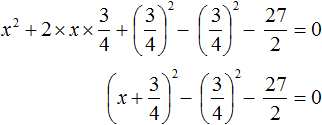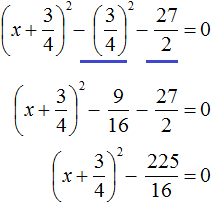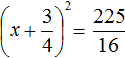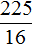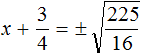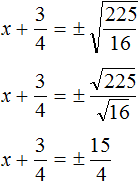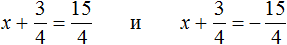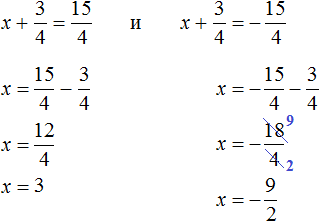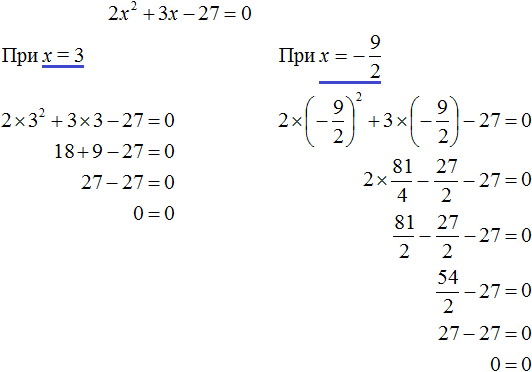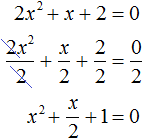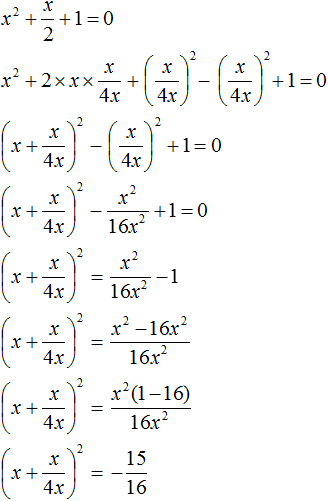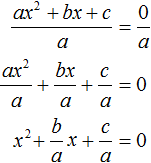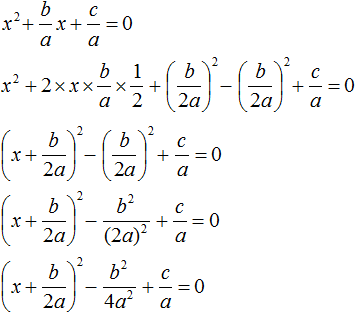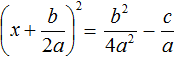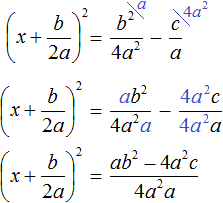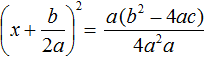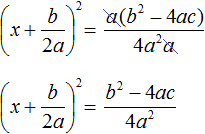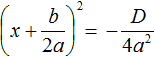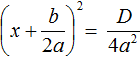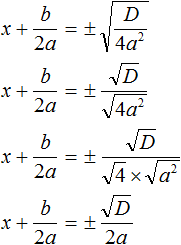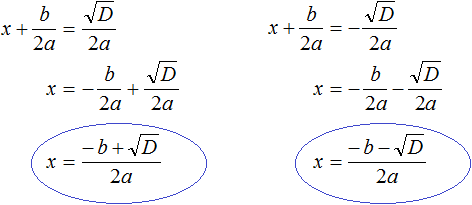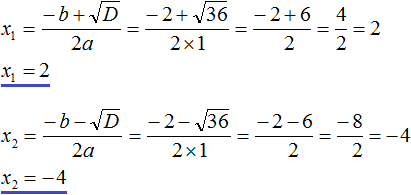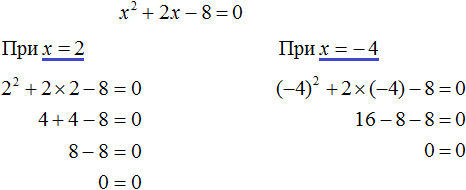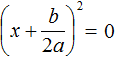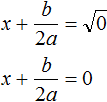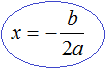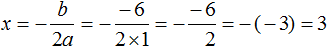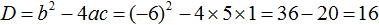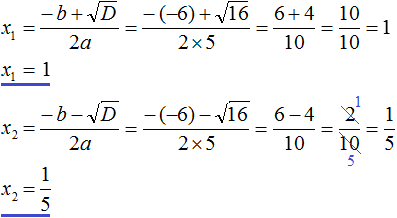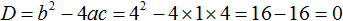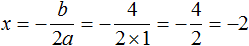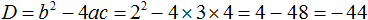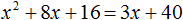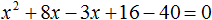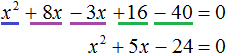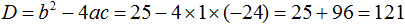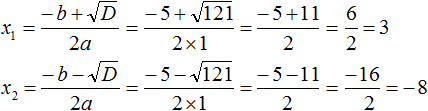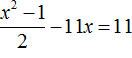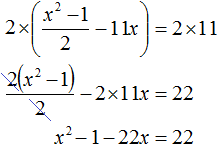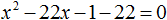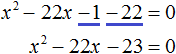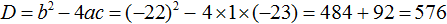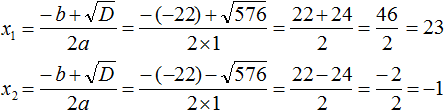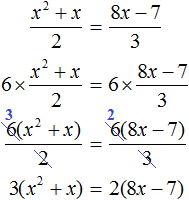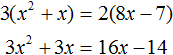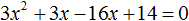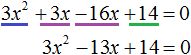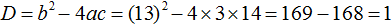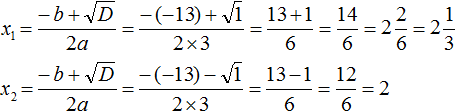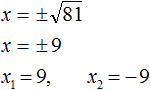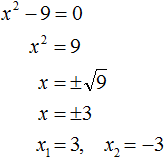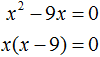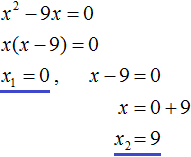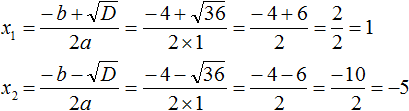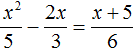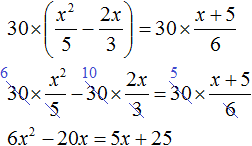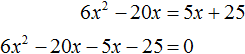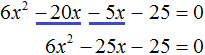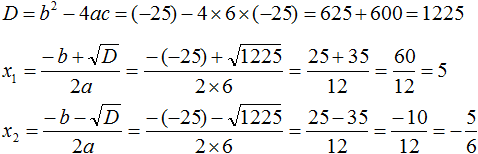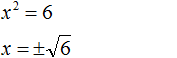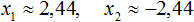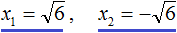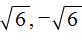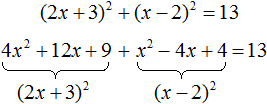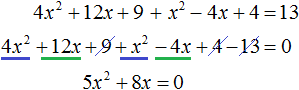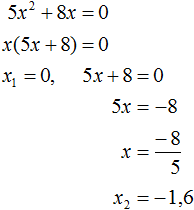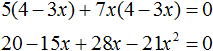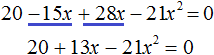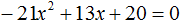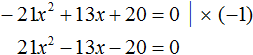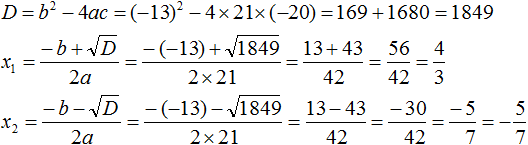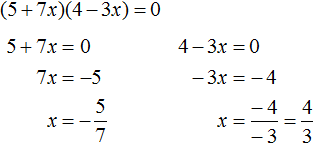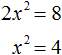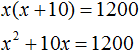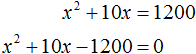Как сделать проверку квадратного уравнения
Квадратное уравнение
Что такое квадратное уравнение и как его решать?
Мы помним, что уравнение это равенство, содержащее в себе переменную, значение которой нужно найти.
Если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение называют уравнением второй степени или квадратным уравнением.
Например, следующие уравнения являются квадратными:
Все тождественные преобразования, которые мы применяли при решении обычных линейных уравнений, можно применять и при решении квадратных.
Итак, в уравнении x 2 − 4 = 0 перенесем член −4 из левой части в правую часть, изменив знак:
У нас переменная x всё ещё во второй степени, поэтому решение необходимо продолжить.
Обычно записывают так: перед квадратным корнем ставят знак «плюс-минус», затем находят арифметическое значение квадратного корня. В нашем случае на этапе когда записано выражение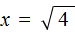 
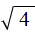
, перед 
следует поставить знак ±
Затем найти арифметическое значение квадратного корня
Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно:
В обоих случаях левая часть равна нулю. Значит уравнение решено верно.
Решим ещё одно уравнение. Пусть требуется решить квадратное уравнение (x + 2) 2 = 25
Решим оба уравнения. Это обычные линейные уравнения, которые решаются легко:
Запишем полностью решение уравнения (x + 2) 2 = 25
Бывает и так, что квадратное уравнение имеет только один корень или вовсе не имеет корней. Такие уравнения мы рассмотрим позже.
Квадратное уравнение бывает дано в разном виде. Наиболее его распространенная форма выглядит так:
Это так называемый общий вид квадратного уравнения. В таком уравнении все члены собраны в общем месте (в одной части), а другая часть равна нулю. По другому такой вид уравнения называют нормальным видом квадратного уравнения.
В квадратном уравнении желательно упорядочивать члены так, чтобы они располагались в таком же порядке как у нормального вида квадратного уравнения.
Если какой-то из коэффициентов равен нулю (то есть отсутствует), то уравнение значительно уменьшается и принимает более простой вид. Такое квадратное уравнение называют неполным. Например, неполным является квадратное уравнение 2x 2 + 6x = 0, в нём имеются коэффициенты a и b (числа 2 и 6 ), но отсутствует свободный член c.
Рассмотрим каждый из этих видов уравнений, и для каждого из этих видов определим свой способ решения.
Для дальнейшего упрощения уравнения воспользуемся ранее изученными тождественными преобразованиями. В данном случае можно разделить обе части на 2
Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно:
В обоих случаях левая часть равна нулю, значит уравнение решено верно.
Также, неполным будет квадратное уравнение, если коэффициент c равен нулю.
Получилось уравнение x(2x + 6) = 0 в котором нужно найти x, при котором левая часть станет равна нулю. Заметим, что в этом уравнении выражения x и (2x + 6) являются сомножителями. Одно из свойств умножения говорит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
В нашем случае равенство будет достигаться, если x будет равно нулю или (2x + 6) будет равно нулю. Так и запишем для начала:
Видим, что второй корень равен −3.
Выполним проверку. Подставим корни 0 и −3 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 0 и −3 левая часть равна нулю, то это будет означать, что уравнение решено верно:
Проще говоря, если в квадратном уравнении вида ax 2 + bx + c = 0 числа b и с равны нулю, то корень такого уравнения равен нулю.
Отметим, что когда употребляются словосочетания « b равно нулю » или « с равно нулю «, то подразумевается, что параметры b или c вовсе отсутствуют в уравнении.
Значит корнем уравнения x 2 − 2x + 1 = 0 является единица. Других корней у данного уравнения нет. В данном случае мы решили квадратное уравнение, имеющее только один корень. Такое тоже бывает.
В данном случае левая часть уже не является квадратом суммы или разности. Поэтому нужно искать другие пути решения.
Заметим, что левая часть уравнения представляет собой квадратный трехчлен. Тогда можно попробовать выделить полный квадрат из этого трёхчлена и посмотреть что это нам даст.
Выделим полный квадрат из квадратного трёхчлена, располагающего в левой части уравнения:
В получившемся уравнении перенесем −4 в правую часть, изменив знак:
Выделим полный квадрат из левой части:
Далее воспользуемся квадратным корнем и узнáем чему равно x
Значит корнем уравнения x 2 − 6x + 9 = 0 является 3. Выполним проверку:
Выделим полный квадрат из левой части:
Перенесём −121 из левой части в правую часть, изменив знак:
Воспользуемся квадратным корнем:
Получили два простых уравнения: 2x + 7 = 11 и 2x + 7 = −11. Решим их:
Пример 5. Решить уравнение 2x 2 + 3x − 27 = 0
Это уравнение немного посложнее. Когда мы выделяем полный квадрат, первый член квадратного трёхчлена мы представляем в виде квадрата какого-нибудь выражения.
Если обе части исходного уравнения умножить или разделить на одно и то же число, то полýчится уравнение равносильное исходному. Это правило сохраняется и для квадратного уравнения.
Перепишем левую часть в виде трёх дробей со знаменателем 2
Сократим первую дробь на 2. Остальные члены левой части перепишем без изменений. Правая часть по-прежнему станет равна нулю:
Выделим полный квадрат.
При представлении члена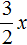 
в виде удвоенного произведения, появление множителя 2 привело бы к тому, что этот множитель и знаменатель дроби 
сократились бы. Чтобы этого не произошло, удвоенное произведение было домножено на 
. При выделении полного квадрата всегда нужно стараться сделать так, чтобы значение изначального выражения не изменилось.
Свернём полученный полный квадрат:
Приведём подобные члены:
Перенесём дробь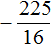 
в правую часть, изменив знак:
Воспользуемся квадратным корнем. Выражение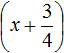 
представляет собой квадратный корень из числа 
Для вычисления правой части воспользуемся правилом извлечения квадратного корня из дроби:
Тогда наше уравнение примет вид:
Полýчим два уравнения:
Значит корнями уравнения 2x 2 + 3x − 27 = 0 являются числа 3 и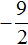 
.
Корень 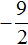удобнее оставить в таком виде, не выполняя деления числителя на знаменатель. Так проще будет выполнять проверку.
Выполним проверку. Подставим найденные корни в исходное уравнение:
В обоих случаях левая часть равна нулю, значит уравнение 2x 2 + 3x − 27 = 0 решено верно.
Такой вид квадратного уравнения называют приведённым квадратным уравнением.
Любое квадратное уравнение вида ax 2 + bx + c = 0 можно сделать приведённым. Для этого нужно разделить обе его части на коэффициент, который располагается перед x². В данном случае обе части уравнения ax 2 + bx + c = 0 нужно разделить на a
Пример 6. Решить квадратное уравнение 2x 2 + x + 2 = 0
Сделаем данное уравнение приведённым:
Выделим полный квадрат:
Получили уравнение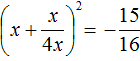 
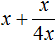
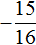
, в котором квадрат выражения 
равен отрицательному числу 
. Такого быть не может, поскольку квадрат любого числа или выражения всегда положителен.
Формулы корней квадратного уравнения
Выделять полный квадрат для каждого решаемого квадратного уравнения не очень удобно.
Можно ли создать универсальные формулы для решения квадратных уравнений? Оказывается можно. Сейчас мы этим и займёмся.
Итак, выделим полный квадрат из левой части уравнения ax 2 + bx + c = 0. Сначала сделаем данное уравнение приведённым. Разделим обе его части на a
Теперь в получившемся уравнении выделим полный квадрат:
Перенесем члены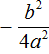 
и 
в правую часть, изменив знак:
Приведём правую часть к общему знаменателю. Дроби, состоящие из букв, привóдят к общему знаменателю методом «крест-нáкрест». То есть знаменатель первой дроби станóвится дополнительным множителем второй дроби, а знаменатель второй дроби станóвится дополнительным множителем первой дроби:
В числителе правой части вынесем за скобки a
Сократим правую часть на a
Поскольку все преобразования были тождественными, то получившееся уравнение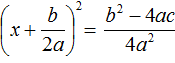 
имеет те же корни, что и исходное уравнение ax 2 + bx + c = 0.
D = b 2 − 4ac = 1 2 − 4 × 2 × 2 = 1 − 16 = −15.
Видим, что D (оно же b 2 − 4ac ) является отрицательным числом. Тогда нет смысла решать уравнение 2x 2 + x + 2 = 0, выделяя в нём полный квадрат, потому что когда мы дойдем до уравнения вида 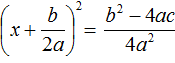, окажется что правая часть станет меньше нуля (из-за отрицательного дискриминанта). А квадрат числа не может быть отрицательным. Следовательно, корней у данного уравнения не будет.
Станóвится понятно почему древние люди считали выражение b 2 − 4ac различителем. Это выражение подобно индикатору позволяет различить уравнение имеющего корни от уравнения, не имеющего корней.
В этом случае говорят, что у исходного уравнения корней нет, поскольку квадрат любого числа не должен быть отрицательным.
В этом случае уравнение будет иметь два корня. Для их вывода воспользуемся квадратным корнем:
Получили уравнение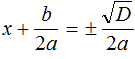 
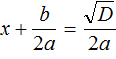
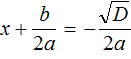
. Из него полýчится два уравнения: 
и 
. Выразим x в каждом из уравнений:
Очерёдность применения формул не важнá.
Прежде чем использовать формулы корней квадратного уравнения, нужно найти дискриминант этого уравнения.
D = b 2 − 4ac = 2 2 − 4 × 1 × (−8) = 4 + 32 = 36
Дискриминант больше нуля. Значит уравнение имеет два корня. Теперь можно воспользоваться формулами корней квадратного уравнения:
Наконец, рассмотрим случай когда дискриминант квадратного уравнения равен нулю. Вернёмся к уравнению 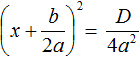. Если дискриминант равен нулю, то правая часть уравнения примет вид:
И в этом случае квадратное уравнение будет иметь только один корень. Воспользуемся квадратным корнем:
D = b 2 − 4ac = (−6) 2 − 4 × 1 × 9 = 36 − 36 = 0
Значит корнем уравнения x 2 − 6x + 9 = 0 является число 3.
Для квадратного уравнения, имеющего один корень также применимы формулы 
и 
. Но применение каждой из них будет давать один и тот же результат.
Применим эти две формулы для предыдущего уравнения. В обоих случаях получим один и тот же ответ 3
Если квадратное уравнение имеет только один корень, то желательно применять формулу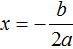 
, а не формулы и . Это позволяет сэкономить время и место.
Пример 3. Решить уравнение 5x 2 − 6x + 1 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Значит корнями уравнения 5x 2 − 6x + 1 = 0 являются числа 1 и 
.
Ответ: 1; .
Пример 4. Решить уравнение x 2 + 4x + 4 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант равен нулю. Значит уравнение имеет только один корень. Он вычисляется по формуле
Пример 5. Решить уравнение 3x 2 + 2x + 4 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант меньше нуля. Значит корней у данного уравнения нет.
Ответ: корней нет.
Пример 6. Решить уравнение (x + 4) 2 = 3x + 40
Приведём данное уравнение к нормальному виду. В левой части располагается квадрата суммы двух выражений. Раскрóем его:
Перенесём все члены из правой части в левую часть, изменив их знаки. В правой части останется ноль:
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Ответ: 3 ; −8.
Пример 7. Решить уравнение 
В получившемся уравнении перенесём 22 из правой части в левую часть, изменив знак. В правой части останется 0
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Ответ: 23; −1.
Пример 8. Решить уравнение 
В получившемся уравнении раскроем скобки в обеих частях:
Теперь перенесём все члены из правой части в левую часть, изменив у них знаки. В правой части останется 0
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
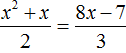
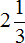
Значит корнями уравнения являются числа 
и 2.
Примеры решения квадратных уравнений
Пример 1. Решить уравнение x 2 = 81
Это простейшее квадратное уравнение, в котором надо определить число, квадрат которого равен 81. Таковыми являются числа 9 и −9. Воспользуемся квадратным корнем для их вывода:
Пример 2. Решить уравнение x 2 − 9 = 0
Это неполное квадратное уравнение. Для его решения нужно перенести член −9 в правую часть, изменив знак. Тогда получим:
Ответ: 3, −3.
Пример 3. Решить уравнение x 2 − 9x = 0
Это неполное квадратное уравнение. Для его решения сначала нужно вынести x за скобки:
Левая часть уравнения является произведением. Произведение равно нулю, если хотя один из сомножителей равен нулю.
Левая часть станет равна нулю, если отдельно x равно нулю, или если выражение x − 9 равно нулю. Получится два уравнения, одно из которых уже решено:
Пример 4. Решить уравнение x 2 + 4x − 5 = 0
Это полное квадратное уравнение. Его можно решить методом выделения полного квадрата или с помощью формул корней квадратного уравнения.
Решим данное уравнение с помощью формул. Сначала найдём дискриминант:
D = b 2 − 4ac = 4 2 − 4 × 1 × (−5) = 16 + 20 = 36
Дискриминант больше нуля. Значит уравнение имеет два корня. Вычислим их:
Пример 5. Решить уравнение 
Умнóжим обе части на наименьшее общее кратное чисел 5, 3 и 6. Это позвóлит избавиться от дробей в обеих частях:
В получившемся уравнении перенесём все члены из правой части в левую часть, изменив знак. В правой части останется ноль:
Приведём подобные члены:
Решим получившееся уравнение с помощью формул:
Пример 6. Решить уравнение x 2 = 6
В данном примере как и в первом нужно воспользоваться квадратным корнем:
Однако, квадратный корень из числа 6 не извлекается. Он извлекается только приближённо. Корень можно извлечь с определённой точностью. Извлечём его с точностью до сотых:
Но чаще всего корень оставляют в виде радикала:
Ответ: 
Пример 7. Решить уравнение (2x + 3) 2 + (x − 2) 2 = 13
Раскроем скобки в левой части уравнения:
В получившемся уравнении перенесём 13 из правой части в левую часть, изменив знак. Затем приведём подобные члены:
Получили неполное квадратное уравнение. Решим его:
Пример 8. Решить уравнение (5 + 7x)(4 − 3x) = 0
Данное уравнение можно решить двумя способами. Рассмотрим каждый из них.
Первый способ. Раскрыть скобки и получить нормальный вид квадратного уравнения.
Приведём подобные члены:
Перепишем получившееся уравнение так, чтобы член со старшим коэффициентом располагался первым, член со вторым коэффициентом — вторым, а свободный член располагался третьим:
Чтобы старший член стал положительным, умнóжим обе части уравнения на −1. Тогда все члены уравнения поменяют свои знаки на противоположные:
Решим получившееся уравнение с помощью формул корней квадратного уравнения:
Произведение равно нулю, если хотя бы один из сомножителей равен нулю. В данном случае равенство в уравнении (5 + 7x)(4 − 3x) = 0 будет достигаться, если выражение (5 + 7x) равно нулю, или же выражение (4 − 3x) равно нулю. Наша задача выяснить при каких x это происходит:
Примеры решения задач
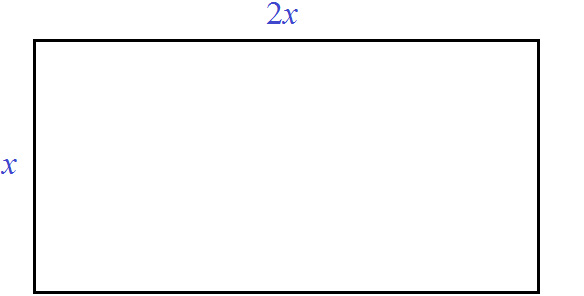
Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху:
Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это:
Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты.
Первое что можно сделать это выполнить умножение в левой части уравнения:
В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением.
Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2
Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м 2
Решение
Решим данное уравнение. Для начала раскроем скобки в левой части:
Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется 0
Решим получившееся уравнение с помощью формул:
x + 10 = 30 + 10 = 40 м
Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30 ) получится 1200 м 2
Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно найти периметр участка.
Периметр прямоугольника это сумма всех его сторон. Тогда:
P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м.
Ответ: длина изгороди огородного участка составляет 140 м.