Как сделать треугольник в unity
Процедурная генерация трёхмерных моделей
Процедурная генерация — замечательная штука! Интереснее всего работать именно с графикой, особенно трёхмерной — сразу видно результат. Всего пары инструкций достаточно, чтобы создать облако треугольников как на картинке выше.
Процедурная генерация моделей может помочь сэкономить размер дистрибутива, добавить кастомизацию игровых персонажей, на худой конец её просто можно использовать для создания спецэффектов.
На примере движка Unity и C# я покажу как можно работать с моделями и превращать текст в графику. Большинство приводимого кода легко портируется на другие фреймфорки и языки.
Треугольник

Начнём с простейшей формы — треугольника. В Unity и во многих других движках используется популярный способ описания моделей: с помощью массивов вершин, треугольников и нормалей. Дополнительно для текстурирования используются uv-координаты вершин. Для работы с моделями есть класс Mesh, в котором для каждого набора данных имеется отдельный массив. В Mesh.vertices хранятся координаты вершин, в Mesh.triangles — индексы вершин группами по три. А в Mesh.normals и Mesh.uv лежат векторы нормалей и координаты uv-карт, индексы которых должны совпадать с индексами соответствующих вершин, т. е. порядок в массивах должен быть одинаковым. Покажу на примере, чтобы было понятнее.
Сделаем функцию, которая на вход принимает три вершины треугольника, а отдаёт готовую модельку. Начнём с основы.
Упаковываем три вершины в массив и передаём мешу. Треугольник описывается элементарно, но есть нюанс, про который нужно помнить. Если смотреть на модель снаружи, то вершины её треугольников должны располагаться по часовой стрелке. Это сделано для того, чтобы во время отрисовки можно было отсечь треугольники, которые «не смотрят в камеру», и обрабатывать их отдельно. Порядок вершин рассчитывается очень просто, поэтому такой способ фильтрации очень эффективен. Если взять произведение двух векторов, то можно найти третий вектор, перпендикулярный плоскости, образуемой сомножителями. Если пробежаться по треугольнику и посчитать произведения, то можно узнать порядок вершин. Кстати эти перпендикулярные вектора нам тоже нужны для описания моделей — это ведь нормали. Нормаль считается следующим образом:
Сначала сделали из трёх точек два вектора, а потом перемножили. Эта нормаль будет одинаковой на всех вершинах треугольника.
Осталось добавить uv-координаты, для трёх вершин это просто.
Ну и всё, треугольник готов. Теперь его можно использовать.
Четырёхугольник

Помимо треугольников есть ещё один популярный примитив для моделирования — четырёхугольник, ну или квад, если вам так больше нравится.
Описать четырёхугольник капельку сложнее, нужно добавить одну вершину с её характеристиками и дополнительный треугольник. Я немного изменил входные параметры по сравнению с треугольником, теперь нужно указывать левый нижний угол и две стороны, с настоящими квадами Mesh в Unity всё равно не работает.
Напоминаю, что вершины по-прежнему записываются по часовой стрелке.
Теперь, когда мы имеем два базовых примитива, мы можем собрать любую модель.
Плоскость

Поэкспериментируем со сборкой моделей на примере плоскости. Возьмём много квадратов и разложим стык в стык.
Лень — двигатель прогресса, поэтому для сборки квадратов в модель будем использовать Mesh.CombineMeshes. Этот метод принимает на вход структуру CombineInstance, в которой можно указать модельку, её индекс и матрицу трансформирования. Для нас важно только первое, остальное игнорируем.
На вход метода подаётся стартовая позиция плоскости, ширина и длина сегмента, количество сегментов. В двойном цикле все квадраты складываются в массив CombineInstance, после чего массив собирается в готовую модель.
Параллелепипед

Раскладывать плитки по плоскости слишком просто, пора перейти к третьему измерению.
Из квадратов хорошо получаются кубы. Даже лучше, с помощью наших псевдоквадов можно делать не только кубы, но и параллелепипеды. Только тссс! Никому не говорите.
Нужно всего шесть четырёхугольников. Зная длину, ширину и высоту параллелепипеда, можно рассчитать все его вершины. Удобно сначала найти два противоположных угла параллелепипеда, а потом от них отстраивать всё остальное. Также имеет смысл отцентрировать модель. Как это выглядит на практике можете посмотреть ниже.
Октаэдр
Октаэдр во многом похож на куб, его вершины очень легко рассчитать, самая большая сложность — сообразить порядок вершин в треугольниках. Октаэдр вписывается в сферу, поэтому имеет смысл строить его по радиусу этой сферы. Все вершины элементарно создаются, так что я не буду здесь останавливаться

Хотя есть ещё один момент. До сих пор многие из вершин в наших моделях дублировались, хотя, как вы возможно слышали, при создании моделей наоборот всегда стараются сократить число вершин и треугольников. Почему же с кубом и октаэдром не так? Покажу на примере, вот код сборки октаэдра с минимально необходимым числом вершин:
В конце я применил Mesh.RecalculateNormals, который автоматически считает нормали, так проще.
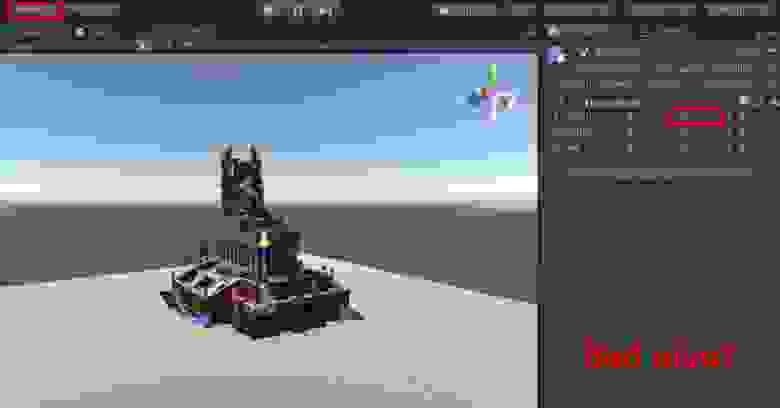
Посмотрите на разницу в освещении между двумя октаэдрами на соседней картинке. В первом случае шэйдеру приходится интерполировать между нормалями, смотрящими совсем в разные стороны, поэтому освещение получается нереалистичным. А во втором случае все грани острые, чёткие. Общие нормали подходят для сфер, гладких поверхностей или если необходимо скрыть малое количество полигонов. А для нашего случая вершин нужно больше.
Тетраэдр

Теперь можно взяться за фигуры поинтереснее. Расчёт вершин даже для простого тетраэдра требует потребует пятёрки по школьной геометрии, поэтому сразу предупреждаю, если не помните что на что делится в синусе, то лучше сначала заглянуть в учебник, как это пришлось сделать мне.
Освежили память? Продолжим.
Пусть наш тетраэдр стоит на одной из граней, тогда противоположную вершину можно добавить сразу:
Остальные вершины должны образовывать равносторонний треугольник. Их координаты можно найти с помощью синусов и косинусов. В Unity есть функции Mathf.Sin и Mathf.Cos, которые ведут расчёт в радианах. Делим окружность на три части и находим на ней три точки:
Из этих вершин уже можно собрать пирамидку, но это не будет тетраэдром, потому что у настоящего тетраэдра все грани одинаковые. Для настоящего тетраэдра основание пирамиды нужно немного уменьшить и сдвинуть ниже. Тут опять пригодятся синусы и косинусы, но чтобы ими воспользоваться, немного смухлюем и подсмотрим один угол в Википедии. «Edge central angle» это угол между радиусами описанной сферы, пересекающими вершины тетраэдра. Кхм, или что-то в этом роде, я успел запутаться пока формулировал мысль. В общем присовокупив этот угол получаем следующий код:
Не так уж и сложно, надеюсь, что все всё поняли. Вот так выглядит всё в итоге, с добавлением масштабирования:
А вот тот же тетраэдр без математики, с захардкоденными вершинами, почувствуйте разницу:
Икосаэдр

Напоследок самое вкусное — икосаэдр. Если выровнять икосаэдр и посмотреть на него под правильным углом, то можно заметить, что две его вершины лежат на одной оси друг под другом, а остальные расположены на двух окружностях.
На каждой окружности их по пять штук, а значит интервал между ними 72 градуса. Смещение между окружностями — 36 градусов. Для выравнивания вершин нам опять понадобится волшебный угол из Википедии: «If two vertices are taken to be at the north and south poles (latitude ±90°), then the other ten vertices are at latitude ±arctan(1/2) ≈ ±26.57°». В переводе на русский это означает, что волшебный угол — арктангенс одной второй.
В конечном итоге всё похоже на тетраэдр, просто окружностей две и немного сложнее сцепка вершин. Сразу добавляем две вершины, считаем одну половинку, затем другую. Собираем в треугольники четырьмя порциями.
Заключение
Если вы внимательно читали код в статье, то наверняка заметили, что там много ненужных вычислений, тот же Mathf.Cos(magicAngle) из примера выше. При желании его можно посчитать только один раз и занести в переменную, это будет не так наглядно и понятно зато быстрее.
Кроме того в генерируемых моделях не самые удобные uv-карты, было бы неплохо их исправить, но для этого придётся переделывать очень много кода, пока и так сойдёт.
А где же сферы и цилиндры? – спросите вы. Редактор статей на Хабрахабре, конечно, замечательный, но навигация по большим объёмам текста в нём не очень удобная, так что оставлю сферы на следующий раз.
Исходники и бинарники для разных платформ можете скачать по ссылкам ниже.
Анатомия мешей
Меш состоит из треугольников, расположенных в 3D-пространстве так, чтобы создать впечатление замкнутого объекта. Треугольник определяется тремя угловыми точками или вершинами. В классе Mesh, все вершины хранятся в одном массиве и каждый треугольник задается с помощью трех целых чисел, которые соответствуют индексам в массиве вершин. Треугольники, также, собраны в единый массив целых чисел, которые берутся группами по три от начала этого массива, так чтобы элементы 0, 1 и 2 определили первый треугольник, 3, 4 и 5 определили второй, и так далее. Любая вершина может быть повторно использована во многих треугольниках по желанию, но есть причины, когда это может быть нежелательно, что объясняется ниже.
Освещение и нормали
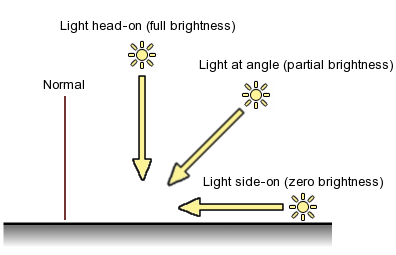
Треугольников достаточно, чтобы определить основную форму объекта, но в большинстве случаев необходима дополнительная информация для отображения сетки. Чтобы объект был правильно затенен при освещении, для каждой вершины должен быть указан вектор нормали. Вектор нормали направлен наружу перпендикулярно поверхности сетки в положении вершины с которой он связан. При расчете затенения, каждая нормаль к вершине сравнивается с направлением падающего света, который также вектор. Если направления этих векторов параллельны, то поверхность получает свет в лоб в этой точке и полная яркость света будет использоваться для затенения. Свет, приходящий точно перпендикулярно вектору нормали не даст освещения поверхности в этой точке. Как правило, свет падает под углом к нормали и поэтому затенение будет где-то между полной яркостью и полной темнотой, в зависимости от угла.
Так как сетка состоит из треугольников, может показаться, что нормали на его углах будут точно перпендикулярны плоскости их треугольника. Однако на самом деле нормали интерполируются между треугольниками с получением среднего значения между соседними углами. Если все три нормали треугольника указывают в одном направлении, то треугольник будет равномерно освещен на всем протяжении. Эффектом того, что разные треугольники равномерно затенены будет то, что края будут очень четкими и отчетливыми. Это именно то, что требуется для модели куба или других объектов с острым краем, но интерполяция нормалей может быть использована для создания плавного затенения, чтобы представить изогнутую поверхность.
Для получения резких ребер, необходимо удвоить вершины в ребре, т.к. оба прилегающих треугольника должны иметь отдельные нормали. Для изогнутых поверхностей вершины смежных треугольников обычно общие, однако нужна некоторая интуиция для определения лучшего направления общей нормали. Нормаль может быть просто средней от нормалей плоскостей окружающих треугольников. Однако для такого объекта как сфера нормаль просто направлена наружу от центра сферы.
Вызывая Mesh.RecalculateNormals, вы можете поручить Unity рассчитать нормали для вас, сделав некоторые предположения о “смысле” геометрии сетки; она предполагает, что вершины общие для нескольких треугольников обозначают гладкую поверхность в то время как удвоенные вершины указывают на четкие края. В большинстве случаев это не плохое приближение, однако RecalculateNormals будет спотыкаться в некоторых ситуациях текстурирования, когда вершины должны быть удвоены, хотя поверхность гладкая.
Текстурирование
Подобно нормалям, текстурные координаты уникальны для каждой вершины и, таким образом, существуют ситуации, когда приходится дублировать вершины для получения различных UV значение вдоль ребра. Очевидный пример, это когда два соседних треугольника используют разделенные части текстуры (например, глаза на текстуре лица). Также, большинство полностью замкнутых объемов потребуют “шов”, где область текстуры заворачивается, и соединяется. Значения UV на одной стороне шва будут отличаться от тех, что на другой стороне.
Математика в Gamedev по-простому. Триангуляции и Triangle.Net в Unity
Всем привет! Меня зовут Гриша, и я основатель CGDevs. Математика – очень крутой инструмент при разработке игр. Но если скажем без понимания векторов и матриц обойтись в принципе сложно, то алгоритмы триангуляций не столь обязательная вещь, но с помощью них решается достаточно большое количество интересных задач. Сегодня хотелось бы поговорить про достаточно важный инструмент в вычислительной геометрии, такой как триангуляции и их применение в игровой индустрии. Кроме того, я написал порт и немного обёрток великолепной библиотеки Triangle.Net для Unity. Если интересно – добро пожаловать под кат. Ссылка на гитхаб прилагается.
Что такое триангуляция?
В общем случае триангуляция – это разбиение геометрического объекта на треугольники. Это понятие само по себе довольно простое. Базовый пример триангуляции в случае игровых движков – это меш. Строго говоря меш может состоять не только из треугольников, но в игровых движках по целому ряду причин берутся именно меши, состоящие из треугольников.
Триангуляции бывают разными, но один из самых популярных видов триангуляций является триангуляция Делоне. Этот вид триангуляции отличается тем свойством, что в окружности, описанной вокруг каждого треугольника, лежат только вершины этого треугольника.
Зачем они нужны?
В целом за пределами игровой индустрии с помощью триангуляций решается большое количество задач. В геймдеве же первая задача, которая приходит на ум – это navigation mesh. Навмеш – это структура данных, которая определяет, по какому пространству игрок может ходить. Он позволяет избежать таких сложных вычислительных задач, как определение столкновений с частью окружения.
Вторая интересная задача, решаемая с помощью триангуляции Делоне в геймдеве – это генерация террейнов и объектов представленных в виде множества точек. Основным плюсом триангуляции Делоне в данном случае является то, что исходя из её свойств она позволяет избежать очень острых треугольников, которые будут мешать и создавать артефакты на тиррейне.
Помимо этого, с помощью триангуляции Делоне с ограничениями и таким алгоритмам как Chew’s second algorithm и Ruppert’s algorithm можно генерировать сетки ещё лучше для тиррейнов и генерировать хорошие сетки для другого применения – метода конечных элементов.
Сам по себе метод конечных элементов, это один из методов с помощью которого решаются задачи прикладной физике. В геймдеве он позволяет решать многие задачи, связанные с симуляцией деформаций, жидкостных симуляций и другого используемого для спец. эффектов. Обычно для записи эффектов в анимации, так как для реалтайма метод обладает слишком высокой вычислительной сложностью. Важной деталью при использовании метода является то, что ошибка метода зависит от углов треугольников в сетке. При наличии в сетке очень острых углов метод даёт огромную ошибку, по этой причине нужны алгоритмы, перечисленные выше.
Ну и конечно же в целом процедурная генерация мешей. Как пример в гитхаб проекте приведена сцена с возможностью рисовать меши. Некоторые физические головоломки используют это применение, как основную механику. Но кроме того алгоритмы триангуляции позволяют с помощью процедурной генерации решать такие задачи, как процедурная разрушаемость и прочее.
Помимо геймдева триангуляции используются в сетях, компьютерном зрении, различных аналитических алгоритмах, а так же в каких задачах вычислительной геометрии, как объединение и исключение многоугольников друг из друга (что бывает полезно часто и в задачах возникающих при разработке игр)
Ear Clipping with Holes
Пожалуй, один из самых простых алгоритмов триангуляции. Даёт не лучшую сетку и обладает большой вычислительной сложностью О(n^2) в худшем случае.
Bowyer–Watson algorithm
Алгоритм, генерирующий триангуляцию Делоне по набору точек. В целом, как и у большинства алгоритмов Делоне при правильной реализации алгоритмическая сложность O( n log n), где n – количество вершин. Но в некоторых случаях может занимать O(n^2).
Минусами относительно Ear Clipping является то, что данный алгоритм строит выпуклую триангуляцию и в базовой реализации не предполагает дыр в получившейся сетке.
Обработка триангуляции Делоне (Delaunay refinement)
Chew’s second algorithm и Ruppert’s algorithm – это алгоритмы, которые позволяют вводить ограничения в триангуляцию Делоне и задать минимальный угол треугольника в сетке. Важной деталью алгоритмов является то, что они могут уйти в бесконечный цикл и гарантировано дают результат при углах между примерно 20.7 градусов и 29 градусов. Возможность задать минимальный угол важна при решении задач, описанных выше.
Chew’s second algorithm реализован в бесплатном пакете www.cs.cmu.edu/
Triangle.Net для Unity
Ну и раз уж с помощью триангуляций можно решать так много крутых задач, то на праздниках захотелось реализовать свою обёртку для Unity, чтобы всегда иметь под рукой удобный инструмент. В данной реализации алгоритм триангуляции в среднем работает за O(n), а в худшем за O(n * log n) – где n-количество вершин. К примеру, при тесте на 1кк вершин случайно разбросанных по квадрату юнити в редакторе на Intel Core i7-8700 строило сетку в среднем за 7.56 секунд.
Основные отличия от оригинальной библиотеки в наличии методов расширений заточенных под Unity, а так же замена double на float во всей библиотеке (+ пара определённых операторов для каста) Double в юнити не имеет особого смысла. Если считать физические симуляции, то я бы использовал отдельное приложение на плюсовой библиотеке, а результат вычислений уже отдавал Unity чисто для визуализации. А также переименован тип Mesh на TriangleNetMesh, чтобы не сбивать относительно Mesh из Unity. Да, они и так в разных неймспейсах, но тем не менее думаю новичков немного сбивал бы тот факт, что мы с помощью одного Mesh получаем другой.
Суть библиотеки в том, что вы сначала должны задать так называемый полигон. Потом на его основе сгенерировать уже меш. Для того, чтобы это работало с юнитёвыми структурами данных было введено несколько методов расширений.
Для демонстрации и примера использования была сделана специальная демо-сцена с возможностью отрисовки мешей. С ней и портом библиотеки можно ознакомится в github проекте.
Спасибо за внимание! Надеюсь, что порт и статья кому-то будут полезны и стало чуть понятнее, зачем нужны триангуляция и знание математики в целом. Буду стараться продолжать раскрывать применения и способы решения разных математических задач в геймдеве. В самой вычислительной геометрии ещё очень много интересного, но помимо ещё есть множество других интересных разделов высшей математики.
Импорт 3D-моделей в Unity и подводные камни
Представляем третью статью нашего цикла о работе с 3D-моделями в Unity. Предшествующие статьи: «Особенности работы с Mesh в Unity» и «Unity: процедурное редактирование Mesh».
В мире компьютерной графики существует множество форматов представления 3D-моделей. Некоторые из них позиционируются как универсальные, другие — как оптимизированные под конкретные задачи или платформы. В любой сфере мечтают работать с универсальным форматом, но реальность говорит нам «нет». Более того, из-за такого зоопарка получается порочный круг: разработчики «универсальных» инструментов придумывают свои внутренние форматы для обобщения предыдущих, увеличивая популяцию и плодя средства преобразования форматов. Так появляется проблема потери или искажения данных при конвертации. Проблема стара как мир (мир IT, конечно), и она не обошла стороной импорт моделей в Unity.
В этой статье мы расскажем о некоторых трудностях, с которыми приходится сталкиваться при работе с моделями в Unity (особенности функционирования ModelImporter, разница представлений 3D-объектов и др.), а также о том, какие инструменты мы создали, чтобы эти трудности преодолеть.
Особенности работы ModelImporter
Напомним, что для API видеокарт минимальный и единственный трехмерный примитив — это треугольник, в то время как геометрия в FBX, например, может быть представлена в виде четырехугольников. Современные 3D-пакеты для создания моделей, как правило, допускают различные уровни абстракции, но и там рендер результата происходит посредством треугольников.
При этом многие инструменты заточены на работу именно с четырехугольниками, что подталкивает 3D-художников использовать этот примитив как основной. В таких случаях в ТЗ часто требуется триангулировать модель перед внедрением. Если триангуляцию не сделали, соответствующий модуль Unity в стандартном режиме выполняет ее автоматически при добавлении файла. Из-за этого появляются ошибки, поскольку алгоритмы триангуляции в разных пакетах реализованы по-разному. При выборе диагонали для разбиения четырехугольника возникает неоднозначность, отсюда большинство проблем, которые можно разделить на две группы.
Первая связана с корректностью отображения формы модели. Так, форма непланарного четырехугольника напрямую зависит от выбора диагонали.

Сюзанна, триангулированная в Blender (Quad Method: Beauty) и в Unity (автоматически при импорте)
Кроме того, алгоритм запекания карты нормалей использует данные о разбиении, из-за чего разница в триангуляции может порождать артефакты в виде креста на блике.

Самокат здорового человека и самокат курильщика
Проблемы второй группы встречаются в текстурной развертке. Например, у нас есть четырехугольник с достаточно тупым для возникновения ошибки углом. При предварительном просмотре в 3D-пакете он разбивается одной из диагоналей на два вполне себе складных треугольника.

Исходный полигон

Полигон, триангулированный в Blender
Однако после импорта в проект обнаруживается, что этот четырехугольник разбит другой диагональю и что один из треугольников либо вообще вырожден, либо близок к тому.

Полигон в Unity с треугольником, близким к вырожденному (правый треугольник практически неотличим от отрезка)
Причиной проблем, связанных с вырожденностью полигонов, являются погрешности в вычислениях с плавающей запятой, а также особенности пиксельной интерполяции при рендеринге. С такими треугольниками происходит черт-те что: они дергаются, каждый кадр меняют цвет. Крайне малая величина поперечного сечения создает сложности при обработке света, из-за чего части динамических объектов могут мерцать. Да и в недетерминированности запекания карты освещения тоже нет ничего хорошего.
Я 3D-пакет, я так вижу
В 3D-моделировании часто возникает разница между фактическим количеством вершин и их количеством в 3D-пакете. Суть проблемы заключается в информации, которая требуется для обработки видеокартой. Структура данных для вершины предопределена и включает в себя позицию, нормаль, касательную, координаты текстурной развертки на каждый канал и цвет. То есть в одну вершину две нормали не запихнуть.
Для некоторых художников же не всегда очевидно, что вершина определяется не только своей позицией. Моделлеры прекрасно знают понятия Hard/Soft Edges и UV Seams, но не все осознают, каким образом они реализованы программно. Дополнительно сбивают с толку 3D-пакеты, которые в стандартном режиме показывают количество вершин как количество уникальных позиций.
Так, обычный примитив Cube геометрически представим 8 вершинами. Однако чтобы корректно передать отражение света от каждой грани и правильно наложить текстуру, в каждом углу куба необходимо по 3 вершины с одинаковой позицией, но разными нормалями и текстурными координатами, поскольку в каждом из углов сходится по 3 ребра. Этому моменту посвятили небольшой блок документации. Там же можно посмотреть примеры.
Метрики куба в Blender

Метрики куба в Unity
Хватит это терпеть!
Столкнувшись с этими и подобными проблемами, мы решили создать инструмент анализа и валидации моделей при импорте в проект Unity. Иначе говоря, кастомный валидатор, который на запрос «Ешь!» ответит: «Не буду! Переделывай», — или выплюнет наборы предупреждений и значений различных параметров, оповещая о том, что ему что-то невкусно.
Для анализа и проверки мы разработали следующий функционал:
Подсчеты количества уникальных позиций вершин, Hard Edges, UV Seams и раскрашенных вершин — необходимы для проверки соответствия задуманной художником модели той, что была импортирована в Unity. Этот функционал также позволяет следить за соблюдением требований к оптимизации модели (например, чтобы количество вершин не превышало определенное значение). Из-за все той же особенности 3D-пакетов, которые показывают по факту количество уникальных позиций, бывают случаи, когда метрика числа вершин в редакторе моделей удовлетворяет этому ограничению, однако после внесения файла в проект может оказаться, что это не так.
Вычисление AABB и его центра — позволяет определить смещение модели относительно начала ее собственной системы координат. Это необходимо для предсказуемого позиционирования ассетов, которые инициализируются в сцене уже во время работы приложения. Так, AABB здания по-хорошему должен иметь minY = 0, а какой-нибудь люстры, которая крепится к потолку — maxY = 0.
Выход координат вершин UV-развертки за диапазон 0.0–1.0 — в большинстве случаев (например, если текстура должна тайлиться на модели) предусмотрен. Часто такой подход используется для представления в сцене множества низкодетализированных мелких объектов (растительности) и/или находящихся вдалеке, а также замощения больших однородных объектов (зданий). В случае тайлинга значениям координат конкретного UV-канала просто обрезают целую часть на уровне шейдера, если Wrap Mode текстуры установлен в Repeat.
Представьте теперь, что вы уложили текстуру в атлас (и накрыли одеялком :3). В шейдер будут приходить уже преобразованные координаты, соответствующие атласу (x * масштаб + смещение). Никакой целой части на этот раз вероятнее всего уже не будет и обрезать будет нечего, а модель залезет на чужую текстуру (одеялко оказалось маленьким). Эта проблема решается двумя способами.
Первый предполагает, что вы заранее обрежете целую часть у координат развертки. В этом случае появляется вероятность взаимоналожения полигонов, о чем мы поговорим ниже.
Второй основывается на том, что тайлинг текстур по своей сути — это метод оптимизации. Вам же никто не запрещает увеличить размер и просэмплировать нужный кусок на всю модель. Однако таким образом полезное пространство атласа будет использовано неэффективно.
Наложения в текстурной развертке — тоже чаще всего не случайны: они нужны, чтобы эффективно использовать площади текстуры. Бывает, что ошибку совершает новичок, старший товарищ это видит, произносит крепкое словцо и новичок больше так не делает. Но бывает, что наложение настолько мелкое и находится в настолько неожиданном месте, что и старший товарищ может его не заметить.
В опытном коллективе незамеченные на базовой развертке ошибки попадают в проект чуть чаще, чем никогда. Другое дело, когда меняются условия использования уже готового контента.
Пример. Мы работали с набором моделей для динамических объектов в игре. Поскольку не было задачи запечь для них свет, в UV-развертке допускались наложения.

Пример базовой UV-развертки с наложениями (показаны красным)
Однако затем мы решили не использовать эти модели как динамические, а расставлять их в качестве статичного декора на уровне. Для оптимизации, как известно, освещение статических объектов в сцене запекают в специальный атлас. Отдельного UV2-канала для карты освещения у этих моделей не было, а качество работы автоматического генератора в Unity нас не устраивало, поэтому мы решили как можно чаще использовать базовую текстурную развертку для запекания.
Здесь и возникли явные проблемы с корректностью освещения. Очевидно, что лучи, попадающие какой-нибудь статуе в глаз, не должны создавать блики на пятой точке на затылке.

Некорректно запеченное освещение модели (слева) и исправленное (справа)
Unity при формировании карты освещения в первую очередь пытается использовать UV2-канал. Если он пустой, то используется основной UV, если и этот пуст, то извините, нате вам исключение. Запечь модели в карту освещения без предварительно подготовленного UV2 в Unity можно двумя способами.
В качестве первого Unity предлагает автоматическую генерацию UV2 на основе геометрии модели. Это быстрее, чем делать вручную, к тому же данный инструмент можно настраивать с помощью нескольких параметров. Но даже несмотря на это, итоговое наложение светотени часто неудовлетворительно для высокодетализированных объектов из-за швов и затеканий в неположенных местах, к тому же упаковка частей такой развертки не самая эффективная.
Второй способ — использовать базовую UV-развертку для запекания. Очень даже привлекательный вариант, поскольку при работе с одной текстурной разверткой меньше вероятность совершить ошибку, чем при работе с двумя. По этой причине мы стараемся минимизировать количество моделей, в базовой UV которых присутствуют наложения. Созданный инструментарий помогает нам это осуществлять.
Проверка текстурной развертки на достаточность заданного пиксельного отступа при заданном разрешении текстуры — более точная валидация UV, основанная на растеризации. Подробнее об этом методе будет рассказано в следующей статье серии.
Подведем итог. Конечно, практически невозможно отследить все нюансы: иногда приходится мириться с несовершенством результата, чтобы выполнить задачу в срок. Однако выявление даже части таких недочетов позволяет ускорить разработку проекта и повысить его качество.