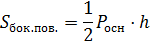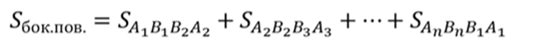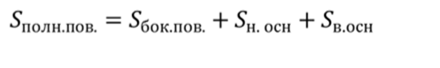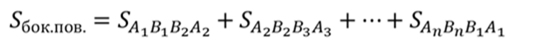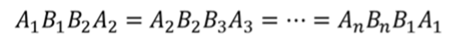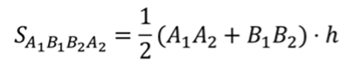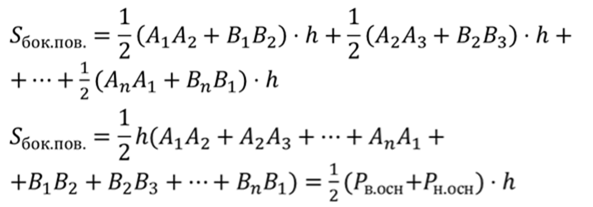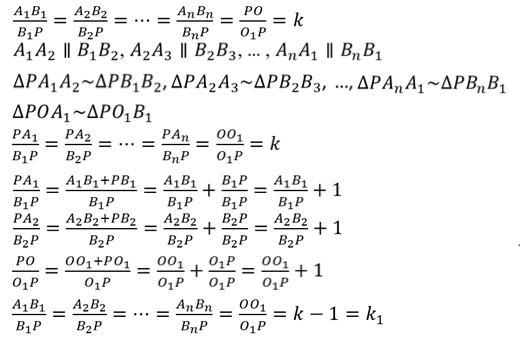Как сделать усеченную четырехугольную пирамиду

Усеченная четырехугольная пирамида

Популярное

Найти подарок для школьника, который будет интересным, полезным, а также не разорит семейный бюджет – возможно ли такое в 2020 году? Рассказываем, чем можно.

В качестве заставки для этой статьи мы предлагаем картинку из популярной телевикторины.

Что общего между октаэдром и кубом?

Знакомые каждому с детства коробочки для Биг-Мака и картошки, стаканчик для Кока-Колы так же делают из бумажных разверток.

Итальянская компания BULGARI (Булгари), основанная в 1884 году, активно использует в рекламных целях геометрическую форму восьмиугольника для.

Можно ли проводить дополнительные школьные занятия по геометрии собирая модели многогранников? Конечно же да. Нас пригласили в школу № 2005 (г. Москва), чтобы показать как.

Источник

Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида

Что такое пирамида в общем случае?

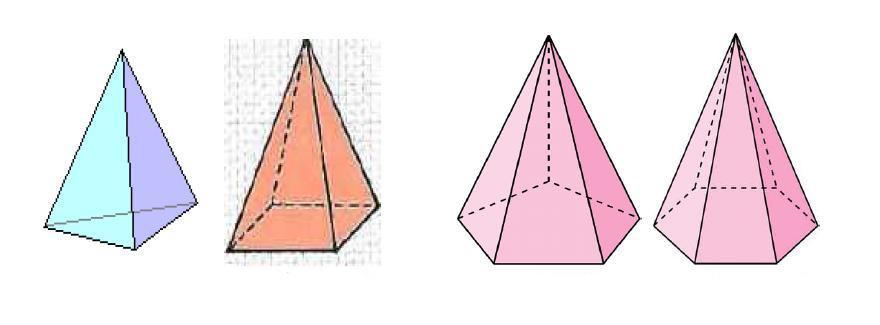
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Правильная четырехугольная пирамида

Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).

Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.

Египетские пирамиды в Гизе являются правильными четырехугольными.

Далее приведем формулы, позволяющие определить все характеристики этой фигуры.

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.

Площадь и объем фигуры

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

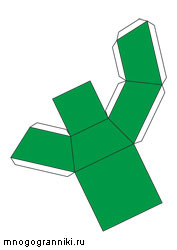
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

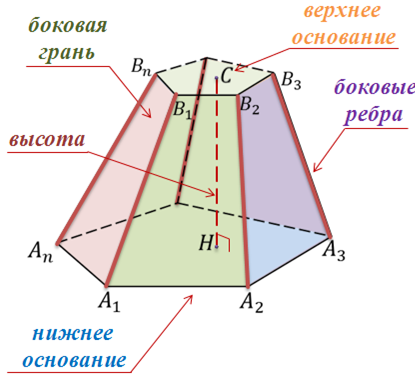
Свойства правильной усеченной четырехугольной пирамиды

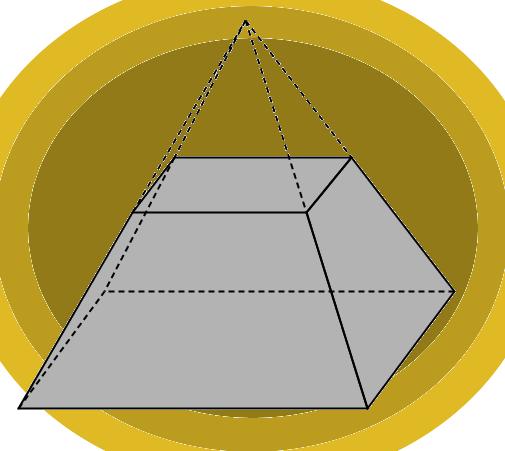
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.

Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:

V = 1/3 × h × (So1 + So2 + √(So1 × So2))

Источник

Усеченная пирамида

Урок 28. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Усеченная пирамида»

На прошлых уроках мы работали с пирамидами. Давайте вспомним, какой многогранник называется пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.

Пирамида называется правильной, если ее основание – правильный многоугольник.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.

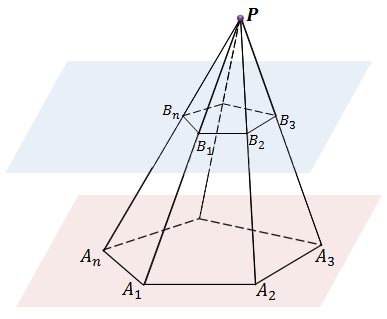
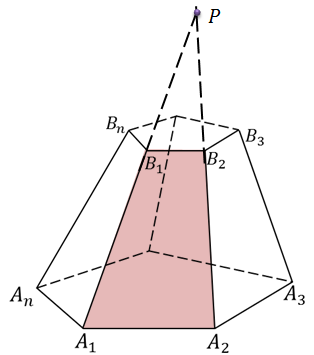
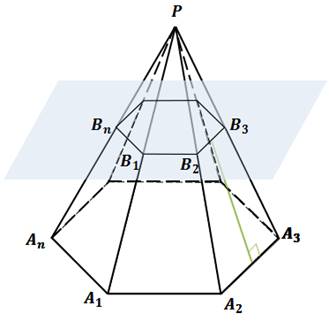
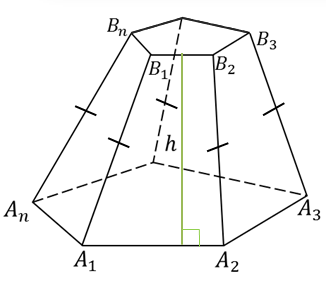
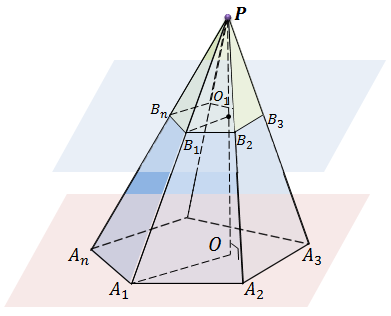
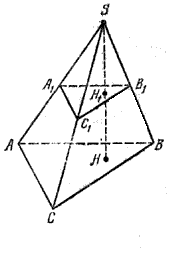
Пусть нам дана пирамида PA₁A₂…A_n. Проведем секущую плоскость β, параллельную плоскости основания пирамиды и пусть эта плоскость пересекает боковые ребра в точках B_1,B₂,…, B_n.

Плоскость β разбивает пирамиду на две фигуры: пирамиду PB₁B₂…B_n и многогранник. Многогранник, гранями которого являются n-угольники A₁A₂…A_n и B₁B₂…B_n, расположенные в параллельных плоскостях и n четырехугольников A₁A₂B₂B₁, A₂A₃B₃B₂,…, A_nA₁B₁B_n называется усеченной пирамидой.

Вокруг нас много примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной пирамиды.клавиши клавиатуры и другие предметы.

Отрезки A₁B₁,…, A_nB_n называются боковыми рёбрами усеченной пирамиды.

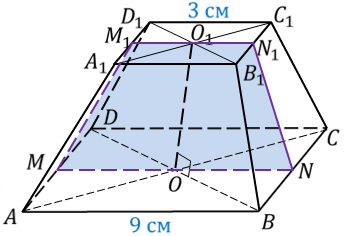
Усеченную пирамиду обозначают так A₁A₂…A_nB₁B₂…B_n. Возьмем на верхнем основании произвольную точку C и из этой точки опустим перпендикуляр на нижнее основание. Этот перпендикуляр называется высотой усеченной пирамиды.

Теперь давайте докажем, что боковые грани усеченной пирамиды – это трапеции.

Для доказательства рассмотрим грань A₁A₂B₂B₁. Понятно, что для других боковых граней доказательство будет проводится аналогично.

Поскольку секущая плоскость проводилась параллельно плоскости основания, то можно записать, что A₁A₂ параллельно B₁B₂. Очевидно, что две другие стороны четырехугольника A₁A₂B₂B₁ не параллельны (они пересекаются в точке P). Получаем, что этот четырехугольник – трапеция. Очевидно, что все остальные боковые грани тоже будут трапециями.

Как и в случае с пирамидой, усеченная пирамида тоже может быть правильной.

Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Основаниями усеченной пирамиды являются правильные многоугольники, а боковые грани – равнобедренные трапеции.

Высоты этих трапеций называются апофемами.

Объединение боковых граней называется боковой поверхностью усеченной пирамиды, а объединение всех граней называется полной поверхностью усеченной пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней.

А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.

Теперь давайте сформулируем и докажем теорему о площади боковой поверхности правильной усеченной пирамиды.

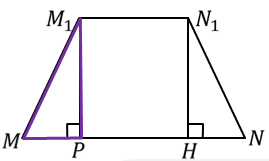
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на апофему.

Запишем формулу для нахождения площади боковой поверхности усеченной пирамиды.

Поскольку усеченная пирамида правильная, значит, ее гранями будут равнобедренные трапеции.

Площадь равнобедренной трапеции равна произведению полусуммы оснований на высоту. Высота боковой грани есть ничто иное как апофема усеченной пирамиды.

Подставим все в исходную формулу, вынесем половину апофемы за скобки, а в скобках сгруппируем стороны по основаниям. Тогда получим, что площадь боковой поверхности будет равна произведению полусуммы периметров оснований усеченной пирамиды на апофему.

Что и требовалось доказать.

Решим несколько задач.

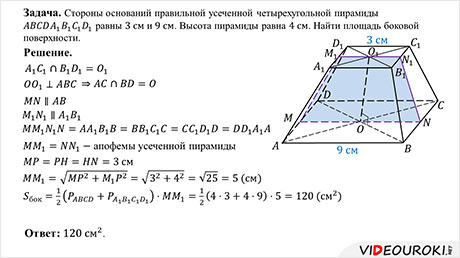
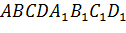
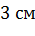
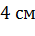
Задача. Стороны оснований правильной усеченной четырехугольной пирамиды равны и . Высота пирамиды равна . Найти площадь боковой поверхности.

Решим еще одну задачу.

Задача. Пирамида пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части.

Что и требовалось доказать.

Решим еще одну задачу.

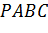
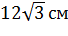
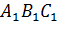
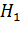
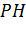
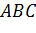
Задача. Правильная треугольная пирамида с высотой и стороной основания равной рассечена плоскостью , проходящей через середину высоты параллельно основанию . Найти площадь боковой поверхности полученной усеченной пирамиды.

Подведем итоги урока. Сегодня на уроке мы познакомились с такими понятиями как усеченная пирамида, правильная усеченная пирамида. Рассмотрели свойства правильной усеченной пирамиды. Решили несколько задач.

Источник

Пирамида и усеченная пирамида

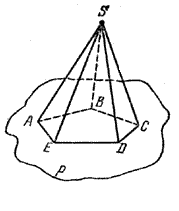
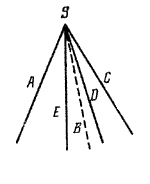
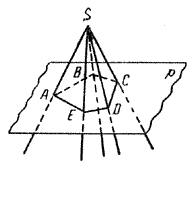
Как можно построить пирамиду? На плоскости р построим какой-либо многоугольник, например пятиугольник ABCDE. Вне плоскости р возьмем точку S. Соединив точку S отрезками со всеми точками многоугольника, получим пирамиду SABCDE (рис.).

Точка S называется вершиной, а многоугольник ABCDE — основанием этой пирамиды. Таким образом, пирамида с вершиной S и основанием ABCDE — это объединение всех отрезков [SM], где М ∈ ABCDE.

Треугольники SAB, SBC, SCD, SDE, SEA называются боковыми гранями пирамиды, общие стороны боковых граней SA, SB, SC, SD, SE — боковыми ребрами.

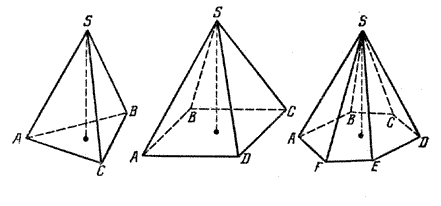
Пирамиды называются треугольными, четырехугольными, п-угольными в зависимости от числа сторон основания. На рис. даны изображения треугольной, четырехугольной и шестиугольной пирамид.

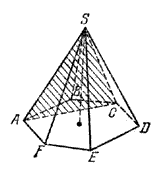
Плоскость, проходящая через вершину пирамиды и диагональ основания, называется диагональной, а полученное сечение — диагональным. На рис. 186 одно из диагональных сечений шестиугольной пирамиды заштриховано.

Отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания, называется высотой пирамиды (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Пирамида называется правильной, если основание пирамиды—правильный многоугольник и вершина пирамиды проектируется в его центр.

Все боковые грани правильной пирамиды — конгруэнтные равнобедренные треугольники. У правильной пирамиды все боковые ребра конгруэнтны.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды. Все апофемы правильной пирамиды конгруэнтны.

Сумма площадей всех боковых граней пирамиды называется площадью боковой поверхности пирамиды и обозначается через S_бок.

Так как боковая поверхность правильной пирамиды состоит из n конгруэнтных граней, то

где Р — периметр основания пирамиды. Следовательно,

т. е. площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Площадь полной поверхности пирамиды вычисляется по формуле

Объем пирамиды равен одной трети произведения площади ее основания S_ocн. на высоту Н:

Вывод этой и некоторых других формул будет дан в одной из последующих глав.

Построим теперь пирамиду другим способом. Пусть дан многогранный угол, например, пятигранный, с вершиной S (рис.).

Проведем плоскость р так, чтобы она пересекала все ребра данного многогранного угла в разных точках А, В, С, D, Е (рис.). Тогда пирамиду SABCDE можно рассматривать как пересечение многогранного угла и полупространства с границей р, в котором лежит вершина S.

Очевидно, что число всех граней пирамиды может быть произвольным, но не меньшим четырех. При пересечении трехгранного угла плоскостью получается треугольная пирамида, у которой четыре грани. Любую треугольную пирамиду иногда называют тетраэдром, что означает четырехгранник.

Усеченную пирамиду можно получить, если пирамиду пересечь плоскостью, параллельной плоскости основания.

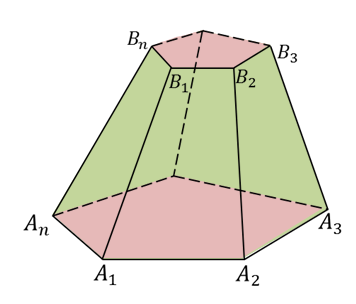
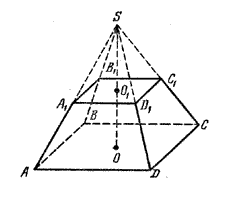
На рис. дано изображение четырехугольной усеченной пирамиды.

Усеченные пирамиды также называются треугольными, четырехугольными, n-угольными в зависимости от числа сторон основания. Из построения усеченной пирамиды следует, что она имеет два основания: верхнее и нижнее. Основания усеченной пирамиды — два многоугольника, стороны которых попарно параллельны. Боковые грани усеченной пирамиды — трапеции.

Высотой усеченной пирамиды называется отрезок перпендикуляра, проведенного из любой точки верхнего основания к плоскости нижнего.

Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и плоскостью сечения, параллельной основанию. Высота боковой грани правильной усеченной пирамиды (трапеции) называется апофемой.

Можно доказать, что у правильной усеченной пирамиды боковые ребра конгруэнтны, все боковые грани конгруэнтны, все апофемы конгруэнтны.

Если в правильной усеченной n-угольной пирамиде через а и b_n обозначить длины сторон верхнего и нижнего оснований, а через h — длину апофемы, то площадь каждой боковой грани пирамиды равна

Так как па = Р и nb_n = Р₁ — периметры оснований усеченной пирамиды, то

т. е. площадь боковой поверхности правильной усеченной пирамиды равна половине произведения суммы периметров ее оснований на апофему.

Сечение, параллельное основанию пирамиды

1) боковые ребра и высота разделятся на пропорциональные части;

2) в сечении получится многоугольник, подобный основанию;

3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Теорему достаточно доказать для треугольной пирамиды.

Так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, то (АВ) || (А₁В₁), (BС) ||( В₁C₁), (AС) || (A₁С₁) (рис.).

Параллельные прямые рассекают стороны угла на пропорциональные части, и поэтому

Соответственные углы треугольников ABC и A₁B₁C₁ конгруэнтны, как углы с параллельными и одинаково направленными сторонами. Поэтому

Площади подобных треугольников относятся, как квадраты соответствующих сторон:

Теорема. Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.

Пусть (черт. 84) В и В₁— площади оснований двух пирамид, H — высота каждой из них, b и b₁ — площади сечений плоскостями, параллельными основаниям и удалёнными от вершин на одно и то же расстояние h.

Согласно предыдущей теореме мы будем иметь:

Источник

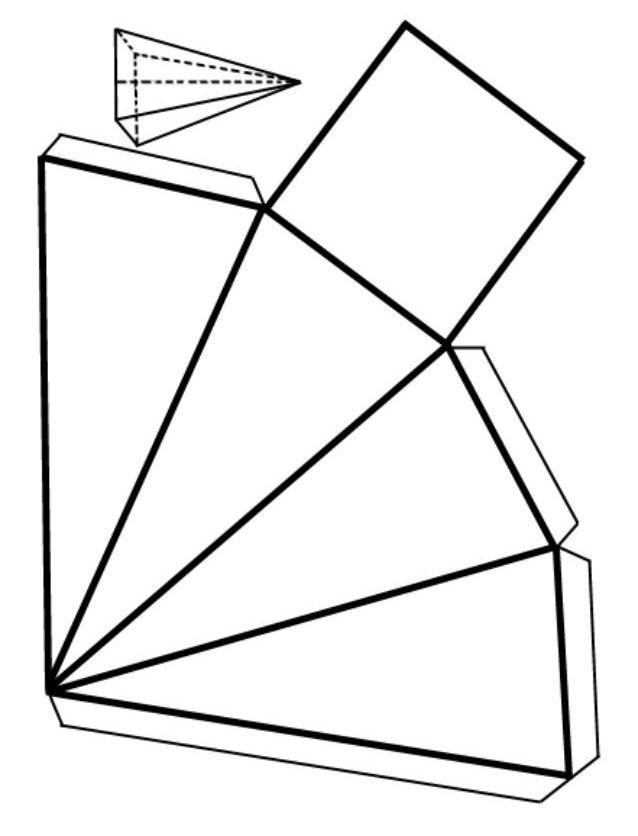
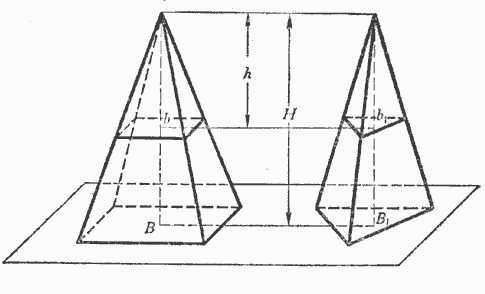
Наклонная пирамида развертка. Усеченная четырехгранная пирамида.

Наклонная пирамида развертка. Усеченная четырехгранная пирамида.

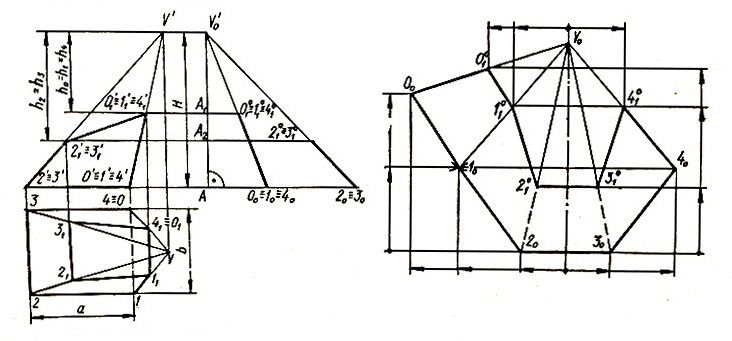
Наклонная усеченная пирамида с четырехугольным основанием показана на рис. 1.

Через точки 0′, 0′₁ и 2′, 2′₁ проводятся прямые до пересечения в точке V’, являющейся вершиной пирамиды.

Рис. 1.

Для определения действительном длины ребер пирамиды через произвольную точку А проводят две перпендикулярные прямые. На горизонтальной линии от точки А откладываются расстояния V₀, V₁,…,V₄ до точек 0₀, 1₀, 2₀,…,4₀. На вертикальной линии откладывается высота пирамиды Н до точки V’₀. Расстояния 0₀V’₀, 1₀V’₀,…, 4₀V’₀ представляют собой действительные длины ребер. Для построения развертки необходимо из произвольной точки V₀ отложить отрезок V₀0₀ = V’₀0₀. Из центров V₀ и 0₀ радиусами соответственно V₀1₀ = V’₀1₀ и 0₀1₀ = 01 описываются дуги до пересечения в точке 1₀. Из центров V₀ и 0₀ описываются дуги радиусами V₀2₀ = V’₀2₀ и 1₀2₀ = 12 до пересечения в точке 2₀. Построение продолжается по описанному способу до получения точки 4₀. Точки 1₀, 2₀, 3₀ и 4₀ последовательно соединяются между собой и каждая с V₀.

Развертка усеченной пирамиды четырехугольной.

Действительная длина ребер малого основания определяется следующим образом. От точки V’₀ откладываются расстояния h₀ = h₁ = h₄ до точки А₁ и h₂ = h₃ до точки А₂. Через точки А₁ и А₂ проводятся горизонтальные прямые до пересечения V’₀0₀ и V’₀2₀ в точках 0 0 ₁ = 1 0 ₁ = 4 0 ₁ и 2 0 ₁ = 3 0 ₁. Из центра V₀ радиусом V’₀0 0 ₁ описывается дуга до пересечения V₀0₀, V₀1₀ и V₀4₀ соответственно в точках 0 0 ₁, 1 0 ₁ и 4 0 ₁. Радиусом V’₀2 0 ₁ из центра V₀ описывается дуга до пересечения V₀2₀ и V₀3₀ в точках 2 0 ₁ и 3 0 ₁, Полученные точки 0 0 ₁, 1 0 ₁, 4 0 ₁ последовательно соединяются, расстояния 0 0 ₁1 0 ₁, 1 0 ₁2 0 ₁ являются действительными длинами ребер малого основания.

Источник