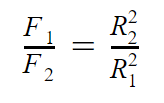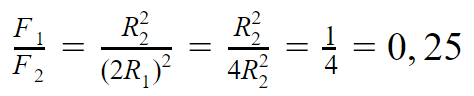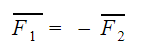Каков физический смысл гравитационной постоянной в законе всемирного тяготения чему

Физический смысл гравитационной постоянной

Гравитационная постоянная – это коэффициент в законе всемирного тяготения:

Закон «всемирного тяготения» был выведен Ньютоном, и описывал «силу притяжения» между двумя телами с массами m1 и m2.

Но каков же физический смысл гравитационной постоянной? Правильно ли мы понимаем суть закона всемирного тяготения?

Не кажется ли вам странным, что закон описывает взаимодействие ДВУХ тел, совершенно не учитывая влияние других? В то время как ВСЕМИРНОЕ тяготение – это явление, охватывающее взаимодействие всех тел во вселенной.

Значение гравитационной постоянной было неизвестно Ньютону. И он даже не знал, каким образом его можно было бы рассчитать. Это сделал другой ученый – Кавендиш – в 1798 году.

В этом небольшом видео очень хорошо демонстрируется сам эксперимент:

Внимательно просмотрев видео и проанализировав данный эксперимент, можно прийти к заключению, что массы шаров тут вообще ни при чем. Никакого «гравитационного притяжения» между ними нет.

Более того, скорее всего, эксперимент с крутильными весами на другой планете даст совсем другое значение «гравитационной постоянной», а значение 6,67 – это локальная константа, характерная именно для Земли, с её скоростью вращения и траекторией движения.

Обратите внимание, как поставлен эксперимент. В нём используются ВЕСЫ. Это очень важная деталь эксперимента. Без неё эксперимент не удастся. Если вы просто подвесите на нитках два шарика, то между ними не будет никакого притяжения. И никакие сверхточные измерения этого не зафиксируют.

А что такое весы? Это гармоническая, самоуравновешивающаяся система, которая балансирует за счет взаимодействия с Землей. И в данном эксперименте мы рассматриваем взаимодействие двух весов, которые стремятся уравновеситься с движением Земли! Однако экспериментатор приписывает эффект притяжения самим шарикам, полностью игнорируя влияние Земли и её движения! И это главная ошибка, которая приводит ко множеству других логических ошибок и неверных выводов.

Физический смысл закона «всемирного тяготения» заключается в том, что вся вселенная – это единая гармоническая система, стремящаяся к равновесию. Отсюда и вытекают все закономерности движений небесных тел и распределения материи во вселенной, то есть все временные и пространственные закономерности.

Но для понимания всей глубины этого универсального закона вселенной недостаточно вычисления константы, нужно уметь чувствовать, осознавать действие этих законов в самом себе. И тогда он становится не просто сухой формулой, а универсальным нравственным законом развития и бытия.

Источник

Физический смысл гравитационной постоянной

Руководитель группы учёных из Международного Бюро Мер и Весов жалуется: «Существует фундаментальная физическая константа, точное значение которой до сих пор не выяснено, а это метрологический и научный тупик. И метрологи ломают копья в постоянных битвах за вычисление точной величины гравитационной постоянной..»

4. Каждое тело притягивает к себе. Если между ними ОДНА сила притяжения, тогда результатом будет разность этих сил, но не сила притяжения одного тела другим. Следовательно, тела притягиваются ДВУМЯ силами, равными по модулю, Но в таком случае бОльшее по массе тело каким-то образом дополняет силу меньшего по массе своей.

5. Исследователей всегда удивлял тот факт, что в афелии (т.е. на максимальном удалении от Солнца) планета может и имеет(а может быть и имеет) перевес центробежной силы над центростремительной, но почему-то планета не уходит в «никуда», а продолжает движение, «возвращаясь» по своей орбите? Так какой же силой она возвращается? Настоящие физики могут объяснить даже необъяснимое, привлекая математику, поэтому они ввели добавочную силу, представляющую собой равнодействующую проекций векторов переносного и относительного движений на плоскость абсолютного движения, и нормальная составляющая переносного ускорения должна «выдать» эту добавочную силу. Понятно? Мне тоже.

Считаем, что на самом деле, никакой добавочной силы нет, а есть взаимосвязанный процесс втягивания(притяжения) гравитационной силой этой планеты в направлении от Солнца к себе в каждый данный момент и выталкивания своей же инертной массы в противоположном (к Солнцу)направлении высвобожденной инерциальной силой инертной массы планеты. И эта сила на многие порядки больше своей силы притяжения, достигшей Солнца, т.к. инертная масса планеты в этом направлении осталась неуравновешенной своей гравитационной силой.

И.Ньютон писал:»Силы, которыми главные планеты постоянно отклоняются от прямолинейного движения и удерживаются на своих орбитах, НАПРАВЛЕНЫ(выделено мной) к Солнцу и обратно пропорциональны квадратам расстояния до его центра»

Считается, что гравитационная постоянная G была введена Пуассоном в уже существующую формулу всемирного тяготения спустя более чем столетие после опубликования трудов Ньютона в связи с переходом к единой метрической системе мер. Т.е. была введена волевым решением в качестве коэффициента пропорциональности, и уже исходя из размерности величин, входящихв формулу, определили её размерность. Численное значение G было получено на основе значения средней плотности Земли, вычисленной Кавендишем.

Чтобы уравновесить силу притяжения между свинцовым и ртутным шарами, нужно положить гирьку 0,7мг, что даёт силу притяжения Fпр.= 6,7388х10^-6н. Если два тела различной массы воздействуют друг на друга одинаковой силой, то логично предположить, что сила F каждого тела обратно пропорциональна их массам.

На основании исходных данных и нашего предположения составляем равенство для силы каждого шара:
Fпр.св.= 6,7388х10^-6н = Gсв./r^2 х Mрт./Mсв.= Fвт.св.х Mрт./Мсв.

Fпр.рт.= 6,7388х10^-6н = Gрт./r^2 х Мсв./Мрт.= Fвт.рт.х Мсв./Мрт. где

Сила притяжения известна из опыта, массы шаров, их радиусы и расстояние между ними известны, вычисляем неизвестные величины:

Gсв. = 2,40172х10^-3 кгм^3/c^2 Gрт. = 1,668х10^-9 кгм^3/c^2

Определяем гравитационные втягивающие силы шаров:

Fвт.св. = Gсв./r^2 = 8,0866х10^-3 н
Fвт.рт. = Gрт./r^2 = 5,6157х10^-9 н
Отсюда уже можно сделать вывод, что сила притяжения свинцового шара является частью его гравитационной втягивающей силы, а гравитационная втягивающая сила ртутного шара является лишь частью своей силы притяжения. Масса свинцового шара больше массы ртутного в 1,2х10^3 раз, а его гравитационная втягивающая сила больше такой же у ртутного в 1,44х10^6 раз, следовательно, при арифметическом росте массы её гравитационная сила растёт геометрически.

Отношение гравитационных втягивающих сил шаров равно квадрату отношения их масс:
Fвт.св./Fвт.рт. = 1,44х10^6 (Mсв./Mрт.)^2 = 1,44х10^6

Следовательно, для нахождения гравитационного эквивалента для любой другой массы, нужно отношение величины этой массы к величине одной из опытных масс возвести в квадрат, и умножить на соответствующий гравитационный эталонный эквивалент по силе:
Gn = (Mn/Mрт.)^2 х Gрт.

Подставляя развёрнутые значения Fпр.св., Fпр.рт., Gсв., Gрт.
отыскиваем собственные ускорения гравитационных втягивающих сил для каждого шара в центре другого.
«Попутно» проявляются численные значения гравитационной постоянной:

G = Gсв./ (Mсв.)^2 = 2,40172х10^-3 кгм^3/c^2 / (6х10^3кг)^2 =6,67144х10^-11м^3/c^2кг

G = Gрт./(Мрт.)^2 = 1,6679х10^-9 кгм^3/c^2 / 25кг^2 = 6,6716х10^-11 м^3/c^2кг

Отметим, что исходным посылом для наших рассуждений была только сила притяжения между ртутным и свинцовым шарами, полученная из опыта. Всё. Никаких формул, относящихся к закону тяготения Ньютона не использовалось. Значение гравитационной постоянной не вводилось, да оно и не появлялось в ходе формулировок, а проявилось в качестве императива-детерминанта поля тяготения каждого шара при вычислении собственных ускорений шаров.

Исходя из полученных формул можно заключить,что при арифметическом росте массы, её гравитационная энергия увеличивается пропорционально квадрату массы:
Gn = G M^2
А из формулы ускорения: а = G M/r^2
предварительно считаем, что гравитационная постоянная это удельное ускорение втягивания собственной гравитационной силой собственной инертной массы, действительное для любой плотности вещества (в системе СИ).

Перейдём к появившейся формуле притяжения одного тела другим:
Fпр. = Fвт. х М1/М2
Каждое тело притягивает другое силой пропорциональной обратному отношению масс. Фактически это другая интерпретация закона тяготения. При этом возникают следствия, которые не проявляются, исходя из прямой пропорциональности взаимодействующих масс. В частности, при вычислении необходимой скорости для спутника Земли, в формуле присутствует и его масса.

Мы определили гравитационные силы, сопровождающие взаимодействие ртутного и свинцового шаров, с их помощью вычислили Гравитационную постоянную, но что означает, что гравитационная втягивающая сила ртутного шара в
6,7388х10^-6 н /5,6157х10^-9 н = 1200 раз меньше своей силы притяжения? Мы же исходили из равенства сил притяжения шаров, и стрелка весов показала её величину?

Эти силы притяжения действительно равны, НО! За чей «счёт»?
Можно было бы считать, что ВСЯ гравитационная втягивающая сила свинцового шара на расстоянии до центра ртутного расходуется на уравновешивание и дополнение силы ртутного шара? Ведь она в точности, в 1200 раз больше силы притяжения, и это она дополняла бы гравитационную силу ртутного шара до необходимой?
Но в таком случае, весы и показали бы силу притяжения 8,0866х10^-3 н, что в десяки раз больше определённой из опыта.
Однако, главное заключается в том, что гравитационная сила свинцового шара 8,0866х10^-3 распределяется пропорционально массам взаимодействующих тел, и кроме силы притяжения со своей стороны, для ртутного ничего гравитационного свинцовый шар добавить не может.

Во взаимодействии ртутного и свинцового шаров неявно участвуют инерциальные силы их инертных масс. Это высвобожденная инерциальная сила инертной массы свинцового шара величиной 6,7388х10^-6 н дополнила гравитационную втягивающую силу ртутного шара до, якобы его,силы притяжения и сдвинула стрелку весов на 0,7 мг. При этом, если бы и свинцовый шар стоял на весах, они бы показали, что он «похудел» за время опыта на 0,7 мг

Гравитационные силы шаров, будь они сами по себе, даже не качнули бы стрелку весов, хотя бы и вплотную посади ртутный шар на свинцовый.

1. Гравитационных эквивалент Земли:

Gз = (Мз / Мсв.)^2 х Gсв.= 2,3825х10^39 кгм^3/c^2

2. Гравитационная втягивающая сила на поверхности Земли:

3. Ускорение на поверхности Земли:

а = Fвт.з./ Мз = 9,8 м/с^2

4. Гравитационная втягивающая сила в точке на расстоянии до Луны:

5. Эта сила распределяется пропорционально массам Земли и Луны:

Fпр.л.= Fз.-л.х Мл./Мз = 1,978х10^20н

6. Ускорение с которым Земля втягивает Луну (напряжённость поля тяготения Земли в любой точке орбиты Луны):

1,978х10^20н / 7,33х10^22кг = 2,7х10^-3 м/с^2

7. Fз.-л. можно определить ещё и как произведение массы Земли на ускорение, с которым Земля втягивает Луну:

Fз.-л. = Мз х 2,7х10^-3 = 1,612х10^22 н

Теперь подставим в п.5 вместо Fз.-л. его произведение:

Fпр.л. = Мз х 2,7х10^-3 х Мл./Мз

но ускорение 2,7х10^-3 м/c^2 = G Мз / r^2 тогда получаем

Fпр.л. = Мз х G х Мз / r^2 х Мл./Мз сокращая Мз, получаем

полноценную формулу закона всемирного тяготения. Т.е в вычисленной силе Fз.-л. уже присутствовала, но неявно, гравитационная постоянная. И не замени мы силу Fз.-л. на равное ей произведение массы на ускорение, то не получили бы «перехода » формулы с обратной пропорциональностью масс в формулу с прямой пропорциональностью взаимодействующих масс, что свидетельствует о равенстве по модулю сил притяжения и инерционных сил взаимодействия (ц.стр. и цб. сил).

Мы исходили из обратной пропорциональности инертных масс, и для получения искомых величин вовсе не требовалась гравитационная постоянная. По массе пробного тела и его гравитационному эквиваленту, радиусу планеты и ускорению на её поверхности можно найти массу любой планеты, не используя гравитационную постоянную.
Однако, она «главное действующее лицо» и не только в законе всемирного тяготения, хотя Ньютон её в закон и не вводил.

Само понятие слова УДЕЛЬНЫЙ связано с единицей свойства тела или единицей объёма, веса и т.п., поэтому можно сказать:

Если в состоянии устойчивого равновесия двух тел существуют силы пропорциональные обратному отношению их инертных масс, то существуют противодействующие им силы, равные по модулю и пропорциональные произведению этих масс. Для каждого тела:

F2 х М1/М2 = G/r^2 M1 х M2

F1 х М2/М1 = G/r^2 M2 Х М1

Каждое небесное тело воздействует и отвечает на воздействие своими гравитационными силами и тем самым запускают работу внутренних сил той же природы каждого тела по вращению и перемещению этих тел. Но это уже, как говорят, другая история.

Источник

Все самое интересное что нужно знать о гравитационной постоянной

Что такое и чему равна гравитационная постоянная

Формула закона всемирного тяготения, известная по курсу школьной механики:

G – коэффициент пропорциональности или гравитационная постоянная;

m_1, m₂ – массы двух тел, испытывающих взаимное притяжение;

r – расстояние между ними.

Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:

Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.

В чём измеряется гравитационная постоянная

Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной – , но её возникновение легко объясняется.

Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём

то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.

После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.

То есть единица измерения гравитационной силы –

и размерность не совпадает с привычной . Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.

Проведём математические вычисления самостоятельно.

Нужно уравнять и .

Получилась требуемая размерность.

Следовательно, постоянная имеет размерность .

Как найти гравитационную постоянную – история открытия

Коэффициент G – универсальная константа, измерение которой осуществляется экспериментальным путём. Доподлинно неизвестно, кто открыл значение гравитационной постоянной, первое употребление в «Трактате по механике» Пуассона датируется 1811 годом.

Работы Ньютона

При публикации закона тяготения в трактате Ньютона отсутствовало явное обозначение константы, характеризующее гравитацию и её действие. Коэффициент не появлялся в работах по физике вплоть до конца восемнадцатого века, его точное значение не было вычислено.

Вместо известной сегодня постоянной присутствовал гравитационный параметр:

M – масса объекта, причём, масса планеты или звезды, так как гравитационный параметр нашёл широкое распространение в астрофизике.

Сегодня для объектов Солнечной системы значение параметра рассчитано точнее, чем гравитационная постоянная G и масса по отдельности, так как она не требует серьёзных экспериментов, вычисляется на основании астрономических наблюдений.

Подробнее о использовании закона всемирного тяготения в астрономии вы можете прочитать в нашей статье.

Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша

Естествоиспытатель Джон Митчел придумал эксперимент для определения массы Земли при помощи крутильных весов, однако не реализовал его. После его смерти идея опыта и аппаратура перешли к английскому физику и химику Генри Кавендишу, который, усовершенствовав прибор, провёл ряд экспериментов и осуществил задумку своего предшественника.

Главенствующая роль в опытах отводилась установке. На метровой нити из меди подвешивалось коромысло длиной 1,8 метра, на его концах устанавливалась пара свинцовых шариков диаметром 5 сантиметров, массой 775 грамм. Чуть выше крепилась поворотная ферма, причём тщательно соблюдалось требование совпадения оси вращения фермы с медной нитью. На концах поворотной штанги находилось по одному большому свинцовому шару диаметром 20 сантиметров, массой 49,5 килограмм. Чтобы избежать влияния конвекционных воздушных потоков, вся установка накрывалась плотным деревянным кожухом. Вследствие взаимодействия лёгкие шарики притягивались к тяжёлым, закручивая нить и отклоняя коромысло. Угол отклонения фиксировался двумя телескопами, а сила упругости нити приравнивалась гравитационному взаимодействию шаров.

Величина определённой силы притяжения составляла 0,17 микроньютона. Если сравнивать это значение с весом маленького шара, то оно меньше последнего примерно в 45 миллионов раз.

В результате своего эксперимента Генри Кавендиш рассчитал среднюю плотность Земли, причём его эксперимент был точным – погрешность измеренного значения в сравнении с современным значением составляет всего 0,7%. Именно Кавендишу приписывают открытие значения гравитационной постоянной, однако он никогда не задавался подобной целью при проведении своих опытов. Очевидно, величина константы определена на основании результатов его эксперимента, но кто сделал это первым, неизвестно.

Измерение гравитационной постоянной

Значение константы, полученное по измеренной Кавендишем плотности, по разным источникам разнится. Британская энциклопедия называет число, равное , с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно , а Олег Павлович Спиридонов в сборнике постоянных приводит значение .

Коэффициент пропорциональности определяли после Генри Кавендиша, причём зачастую его установку модернизировали новыми материалами. Например, в 1872 году Корню и Байль для измерения гравитационной постоянной использовали платиновые маленькие шарики и стеклянные, наполненные ртутью, большие. Результаты опыта показали значение

Современная история изменений гравитационной постоянной

Гравитационная постоянная – десятичная дробь, её значение постоянно уточняется, причём измерение коэффициента G происходит путём усовершенствования прибора Митчела и улучшения методов наблюдения. Например, в 2018 году учёные из России и Китая проводили опыты на установках разной конструкции. В первой группе применялся метод «time of swing» (TOS), где коэффициент пропорциональности зависит от колебательной частоты весов. Во второй – метод «angular acceleration feedback» (AAF), где угловое ускорение независимо вращающихся коромысел шаров измеряется системой управления с обратной связью, при этом нить поддерживается незакрученной.

Комитет по данным для науки и техники (CODATA) рекомендовал на 2020 год значение коэффициента пропорциональности, равное:

Таким образом, гравитационная постоянная всё время уточняется, требуя новые, более точные способы измерения и вычисления.

Источник

Закон всемирного тяготения

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Гравитационное взаимодействие

Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.

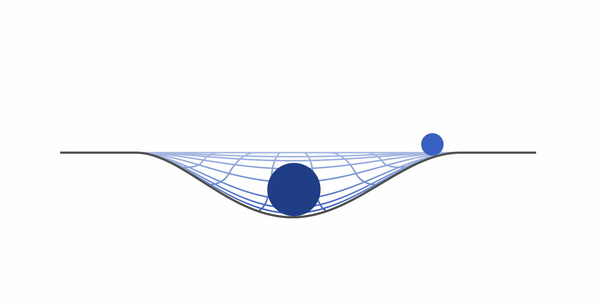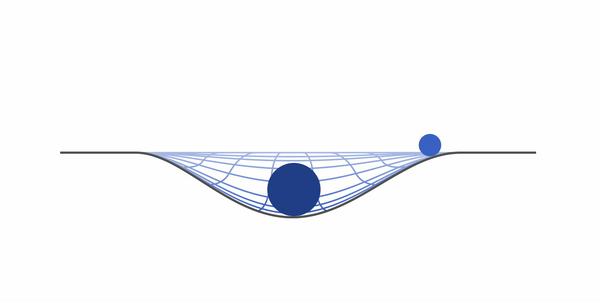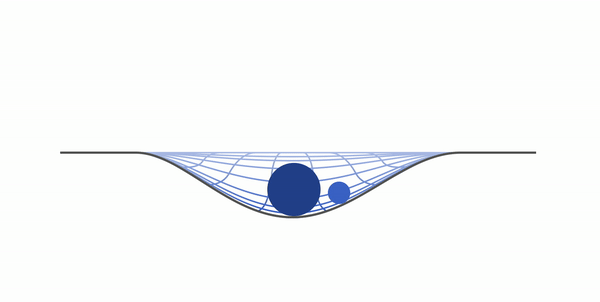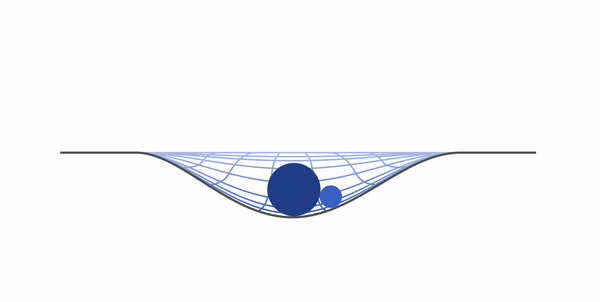
Возьмем два тела — одно с большой массой, другое с маленькой. Натянем гигантское полотно ткани и положим на него тело с большей массой. После чего положим туда тело с массой поменьше. Мы будем наблюдать примерно такую картину:

Маленькое тело начнет притягиваться к тому, что больше, — это и есть гравитация. По сути, Земля — это большой шарик, а все остальные предметы — маленький (даже если это вовсе не шарики).

Гравитационное взаимодействие универсально. Оно справедливо для всех видов материи. Гравитация проявляется только в притяжении — отталкивание тел гравитация не предусматривает.

Из всех фундаментальных взаимодействий гравитационное — самое слабое. Хотя гравитация действует между всеми элементарными частицами, она настолько слаба, что ее принято не учитывать. Все дело в том, что гравитационное взаимодействие зависит от массы объекта, а у частиц она крайне мала. Эту зависимость впервые сформулировал Исаак Ньютон.

Закон всемирного тяготения

В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей.

Задачка раз

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?

Решение

По закону всемирного тяготения сила притяжения планеты к звезде обратно пропорциональна квадрату радиуса орбиты. Таким образом, в силу равенства масс отношение сил притяжения к звезде первой и второй планет обратно пропорционально отношению квадратов радиусов орбит:

По условию, у первой планеты радиус орбиты вдвое больше, чем у второй, то есть R₁=2R₂.

Ответ: отношение сил притяжения первой и второй планет к звезде равно 0,25.

Задачка два

У поверхности Луны на космонавта действует сила тяготения 144 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?

Решение

По закону всемирного тяготения сила притяжения космонавта со стороны Луны обратно пропорциональна квадрату расстояния между ним и центром Луны. У поверхности Луны это расстояние совпадает с радиусом спутника. На космическом корабле, по условию, оно в три раза больше. Таким образом, сила тяготения со стороны Луны, действующая на космонавта на космическом корабле, в 9 раз меньше, чем у поверхности Луны, то есть:

Ответ: на расстоянии трех лунных радиусов от центра сила притяжения космонавта будет равна 16 Н.

Правильно говорить не «на тело действует сила тяготения», а «Земля притягивает тело с силой тяготения».

Ускорение свободного падения

Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.

Сила тяжести — сила, с которой Земля притягивает все тела.

Сила тяжести

F — сила тяжести [Н]

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

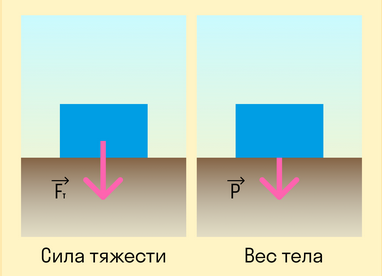
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.

Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.

На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.

Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:

Приравниваем правые части:

Делим на массу левую и правую части:

Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.

Закон всемирного тяготения

g — ускорение свободного падения [м/с 2 ]

M — масса планеты [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.

Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.

Но разве это не зависит еще и от массы предмета?

Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.

Третий закон Ньютона

Третий закон Ньютона обобщает огромное количество опытов, которые показывают, что силы — результат взаимодействия тел.

Он звучит так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Если попроще — сила действия равна силе противодействия.

Если вам вдруг придется объяснять физику во дворе, то можно сказать и так: на каждую силу найдется другая сила. 🙈

Третий закон Ньютона

F₁ — сила, с которой первое тело действует на второе [Н]

F₂ — сила, с которой второе тело действует на первое [Н]

Так вот, для силы тяготения третий закон Ньютона тоже справедлив. С какой силой Земля притягивает тело, с той же силой тело притягивает Землю.

Задачка для практики

Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?

Решение

Согласно третьему закону Ньютона, сила, с которой Земля притягивает мяч, равна силе, с которой мяч притягивает Землю.

Ответ: мяч притягивает Землю с силой 5 Н.

Поначалу это кажется странным, потому что мы ассоциируем силу с перемещением: мол, если сила такая же, то на то же расстояние подвинется Земля. Формально это так, но у мяча масса намного меньше, чем у Земли. И Земля смещается на такое крошечное расстояние, притягиваясь к мячу, что мы его не видим, в отличие от падения мяча.

Если каждый брошенный мяч смещает Землю на какое-то расстояние, пусть даже крошечное, возникает вопрос — как она еще не слетела с орбиты из-за всех этих смещений. Но тут как в перетягивании каната: если его будут тянуть две равные по силе команды, канат никуда не сдвинется. Так же и с нашей планетой.

Источник