Теоретическая механика:
Движение материальной точки

Смотрите также решения задач по теме «Динамика материальной точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

§ 41. Основной закон динамики точки

Точка, движение которой ничем не ограничено, называется свободной. Свободная точка под действием приложенных сил может двигаться в каком угодно направлении. Задачи, в которых рассматривается свободная точка, решаются при помощи основного уравнения динамики (жирным выделены векторные величины)
(а) P = ma.

Если на точку действует только одна сила Р (примером такого движения может служить так называемое свободное падение – движение точки под действием силы тяжести в безвоздушном пространстве), то векторное уравнение (а) заменяется скалярным уравнением
(б) P = ma,
выражающим зависимость между модулями силы и ускорения.

Векторное равенство (в) заменяется двумя или тремя скалярными равенствами.

Если система сил, приложенных к точке, – пространственная, то вместо векторного уравнения (в) составляется три скалярных уравнения проекций на оси х, у и z.

§ 42. Применение принципа Даламбера к решению задач на прямолинейное движение точки

Обычно в задачах по динамике рассматривают так называемые несвободные материальные точки – материальные точки, движение которых ограничивается различными связями.

Приступая к решению задач, в которых рассматривается несвободная материальная точка, нужно прежде всего выявить действующие на точку активные силы (движущие силы и силы сопротивления), а также реакции связей (пассивные силы).

Выявив действующие силы, необходимо определить, находятся они в равновесии или нет? Этот вопрос в зависимости от заданных условий решается двояко.

Если, например, известно, что точка движется равномерно и прямолинейно, значит система сил уравновешена; если же известно, что точка двигается неравномерно или имеет криволинейную траекторию, то система сил неуравновешена (первая задача динамики; Е. М. Никитин, § 76).

Если система сил задана (все силы системы известны), то, определив проекции сил на оси координат, можно установить равновесие или неравновесие системы. В случае когда суммы проекций всех сил на каждую из осей равны нулю, заданная система сил уравновешена. Когда же сумма проекций всех сил хотя бы на одну из осей не равна нулю, система сил неуравновешена. В первом случае точка движется равномерно и прямолинейно, во втором случае – имеет ускорение (вторая задача динамики).

При решении различных технических задач особенно важное значение приобретает случай, когда на материальную точку действует неуравновешенная система сил. В подобных случаях целесообразно решать задачи, применяя так называемый метод кинетостатики или принцип Даламбера (Е. М. Никитин, § 78), который формулируется так: активные силы, реакции связей и сила инерции образуют уравновешенную систему сил.

Применяя принцип Даламбера, необходимо очень хорошо понимать сущность силы инерции (Е. М. Никитин, § 79). Нужно помнить,

во-первых, что сила инерции, численно равная произведению массы точки на приобретенное ускорение, всегда направлена в сторону, противоположную вектору ускорения;

во-вторых, что сила инерции в действительности не приложена к рассматриваемой в задаче материальной точке; она условно прикладывается к этой точке; фактически сила инерции приложена к двигающему телу или к связи;

в-третьих, что равновесие сил, которое образуется после добавления силы инерции к силам, приложенным к точке, – равновесие фиктивное, но оно позволяет воспользоваться для решения задачи уравнениями равновесия из статики.

При решении задач с помощью метода кинетостатики рекомендуется придерживаться такой последовательности:

1) выделить точку, движение которой рассматривается, и изобразить ее на рисунке;

2) выявить все активные силы и изобразить их приложенными к точке на рисунке;

3) освободить точку от связей, заменить связи их реакциями и также изобразить их на рисунке;

4) добавить к полученной системе сил силу инерции;

5) рассмотреть образовавшуюся уравновешенную систему сил и в зависимости от вида системы сил выбрать наиболее рациональный способ решения: графический, графо-аналитический или аналитический (методом проекций).

§ 43. Применение принципа Даламбера к решению задач на криволинейное движение точки

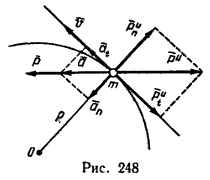
Как известно из кинематики, при движении материальной точки по криволинейной траектории ее ускорение a имеет два составляющих ускорения: a_t – касательное (тангенциальное) и a_n – нормальное (центростремительное).

Из динамики уже известно, что ускорение a, приобретенное точкой, есть результат действия определенной системы сил. Равнодействующая P этой системы и ускорение a (рис. 248) находятся в зависимости, выражающей основной закон динамики точки:
P = ma.

Числовое значение нормальной (центробежной) силы инерции можно выражать следующими формулами:
(1) P_n и = ma_n.

Заменим здесь a_n = v 2 /R:
(2) P_n и = mv 2 /R.

Если материальная точка, рассматриваемая в задаче, связана с каким-либо вращающимся телом, то скорость точки удобнее выражать через угловую скорость тела v=ωR и тогда
(3) P_n и = mω 2 R.

Если в последней формуле выразить массу точки через ее вес m=G/g, а угловую скорость – в об/мин ω=πn/30, то
P_n и = Gπ 2 n 2 R/(900g).

Здесь π 2 ≈g (9,86≈9,81), поэтому формуле можно придать такой вид
(4) P_n и ≈ Gn 2 R/900.

Эта формула дает приближенное значение центробежной силы инерции, но она очень удобна при решении многих задач.

Последовательность решения задач на криволинейное движение точки при помощи метода кинетостатики та же, что в предыдущем параграфе.

Источник

Теоретическая механика:
Кинематика точки

Смотрите также решения задач по теме «Кинематика точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.

* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).

В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.

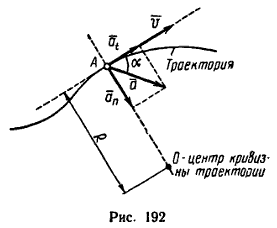
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).

Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.

Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением a_t – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).

Числовое значение касательного ускорения в общем случае определяется по формуле
a_t = dv/dt или a_t = f»(t).

Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением a_n – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).

Числовое значение нормального ускорения определяется в общем случае по формуле
a_n = v 2 /R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.

После того как определены касательное и нормальное ускорения, легко определить и ускорение a ( полное ускорение точки ).

Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(a_t 2 + a_n 2 ).

Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = a_n/a; cos α = a_t/a; tg α = a_n/a_t.

Но можно сначала определить направление полного ускорения a использовав формулу tg α = a_n/a_t,
а затем найти числовое значение a:
a = a_n/sin α или a = a_t/cos α.

Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.

Наличие касательного ускорения (a_t≠0) или его отсутствие (a_t=0) определяют соответственно неравномерность или равномерность движения точки.

Наличие нормального ускорения (a_n≠0) или его отсутствие (a_n=0) определяют криволинейность или прямолинейность движения точки.

Движение точки можно классифицировать так:
а) равномерное прямолинейное (a_t = 0 и a_n = 0);
б) равномерное криволинейное (a_t = 0 и a_n ≠ 0);
в) неравномерное прямолинейное (a_t ≠ 0 и a_n = 0);
г) неравномерное криволинейное (a_t ≠ 0 и a_n ≠ 0).

Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.

Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.

§ 27. Равномерное прямолинейное движение точки

Уравнение равномерного движения имеет вид
(а) s = s₀ + vt
или в частном случае, когда начальное расстояние s₀=0,
(б) s = vt.

В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s₀ и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.

При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.

§ 28. Равномерное криволинейное движение точки

Если a_t = 0 и a_n ≠ 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
a_n = v 2 /R,
где R – радиус кривизны траектории.

В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
a_n = v 2 /r = const.

Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2πr/T = πd/T.

§ 29. Равнопеременное движение точки

Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s₀ + v₀t + a_tt 2 / 2.

Здесь s₀ – расстояние точки от исходного положения в момент начала отсчета; v₀ – начальная скорость и a_t – касательное ускорение – величины численно постоянные, a s и t – переменные.

Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v₀ + a_tt.

Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s₀, v₀, a_t и три переменные: s, v, t.

Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).

Если неизвестные входят в оба основных уравнения, например, неизвестны a_t и t, то для удобства решения таких задач выведены вспомогательные формулы:

после исключения a_t из (1) и (2)
(3) s = s₀ + (v + v₀)t / 2;

В частном случае, когда начальные величины s₀=0 и v₀=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = a_tt 2 / 2;
(6) v = a_tt;
(7) s = vt / 2;
(8) s = v 2 / (2a_t).

Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.

§ 30. Неравномерное движение точки по любой траектории

§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме

Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).

Движение точки в пространстве задается тремя уравнениями:
x = f₁(t);
(1) y = f₂(t);
z = f₃(t);

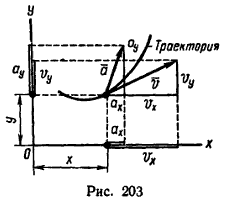
Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f₁(t);
y = f₂(t);

Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).

Если закон движения точки задан в координатной форме, то:

а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;

б) числовое значение скорости точки находится из формулы
v = sqrt(v_x 2 + v_y 2 )
после предварительного определения проекции (см. рис. 203) скорости на оси координат
v_x = dx/dt и v_y = dy/dt;

в) числовое значение ускорения находится из формулы
a = sqrt(a_x 2 + a_y 2 )
после предварительного определения проекций ускорения на оси координат
a_x = dv_x/dt и a_y = dv_y/dt;

г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.

§ 32. Кинематический способ определения радиуса кривизны траектории

При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну ) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
a_n = v 2 /R,
выражающую числовое значение нормального ускорения.

Скорость v точки определяется по формуле
(б) v = sqrt(v_x 2 + v_y 2 ).

Таким образом, если закон движения точки задан уравнениями
x = f₁(t);
y = f₂(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:

1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
v_x = f₁‘(t);
v_y = f₂‘(t).

4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
a_x = f₁»(t) = v_x‘;
a_y = f₂»(t) = v_y‘.

6. Подставить в (в) значения a 2 и a_t 2 и найти a_n.

7. Подставив в (а) найденные значения v 2 и a_n, получить радиус кривизны R.

Источник

Механическое движение и его характеристики

теория по физике 🧲 кинематика

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

По характеру движения точек тела выделяют три вида механического движения:

По типу линии, вдоль которой движется тело, выделяют два вида движения:

По скорости выделяют два вида движения:

По ускорению выделяют три вида движения:

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

Способы описания механического движения

Описать механическое движение можно двумя способами:

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

Перемещение

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет вид:

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

Точка В имеет координаты (5; 10).

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид :

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник