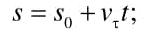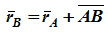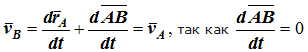Частные случаи движения точки

— уравнение скорости, a_t=0 и a_n=0, — уравнение ускорения.

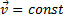
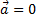
2.Неравномерное прямолинейное движение– это движение где скорость постоянна по направлению, но изменяется по модулю:

Равномерное криволинейное движение точки

Равномерное криволинейное движение- скорость постоянно по модулю и не постоянно по направлению:

Равномерное движение по окружности.

Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d =2r – диаметр), а время равно периоду, т.е. t =T. Выражение скорости примет вид

(29) v = 2πr/T = πd/T., где r – радиус окружности, 2πr- длинна окружности, Т – период – это время однократного оборота по окружности.

Если вектор a_t=const (касательное ускорение постоянно как по модулю, так и по направлению), то a_n=0. Такое движение называется равнопеременным и прямолинейным.

Уравнение равнопеременного движения независимо от его траектории имеет вид

Здесь s₀ – расстояние точки от исходного положения в момент начала отсчета; v₀ – начальная скорость и a_t – касательное ускорение – величины численно постоянные, a s и t – переменные.

Числовое значение скорости точки в любой момент времени определяется из уравнения

Уравнения (30) и (31) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s₀, v₀, a_t и три переменные: s, v, t.

Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).

Если неизвестные входят в оба основных уравнения, например, неизвестны a_t и t, то для удобства решения таких задач выведены вспомогательные формулы: после исключения a_t из (30) и (31)

после исключения t из (30) и (31)

Если же постоянным остается только числовое значение касательного уравнения

a_t = dv/dt = f'(t) = const, то a_n≠0 и такое движение точки называется равнопеременным криволинейным.

При a_t>0 движение точки называется равноускоренным,

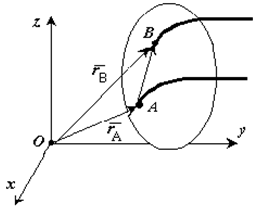
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

Доказательство.

Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением

Траектория точки А– это кривая, которая задается функцией r_A(t), а траектория точки B– это кривая, которая задается функцией r_B(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.

Продифференцируем по времени выражение

Продифференцируем по времени скорость и получим выражение a_B = a_A. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Так как точки А и В были выбраны произвольно, то из найденных результатов следует, что у всех точек тела их траектории, а также скорости и ускорения в любой момент времени будут одинаковы. Таким образом, теорема доказана.

Из теоремы следует, что поступательное движение твердого тела определяется движением какой-нибудь одной из его точки.

При поступательном движении общую для всех точек тела скорость 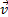называют скоростью поступательного движения тела, а ускорение — ускорением поступательного движения тела. Векторы и можно изображать приложенными в любой точке тела.

Дата добавления: 2018-05-09 ; просмотров: 2317 ; Мы поможем в написании вашей работы!

Источник

Скорость и ускорение при криволинейном движении

. (1.8)

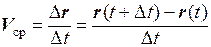
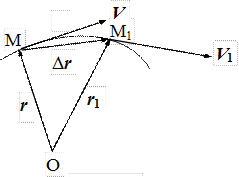
Направление средней скорости V_ср совпадает с направлением вектора Dr.

Предел средней скорости при Dt ® 0, т. е. производная радиуса – вектора r по времени

(1.9)

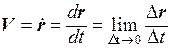
называется истинной или мгновенной скоростью материальной точки. Вектор V направлен по касательной к траектории движущейся точки.

Ускорением а называется вектор, равный первой производной вектора скорости V или второй производной радиуса – вектора r по времени:

(1.10)

(1.11)

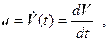
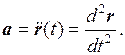
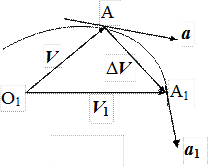
Отметим следующую формальную аналогию между скоростью и ускорением. Из произвольной неподвижной точки О₁ будем откладывать вектор скорости V движущейся точки во всевозможные моменты времени (рис. 1.3).

Конец вектора V называется скоростной точкой. Геометрическое место скоростных точек есть кривая, называемая годографом скорости. Когда материальная точка описывает траекторию, соответствующая ей скоростная точка движется по годографу.

Рис. 1.2 отличается от рис. 1.3 только обозначениями. Радиус – вектор r заменен на вектор скорости V, материальная точка – на скоростную точку, траектория – на годограф. Математические операции над вектором r при нахождении скорости и над вектором V при нахождении ускорения совершенно тождественны.

Скорость V направлена по касательной траектории. Поэтому ускорение a будет направлено по касательной к годографу скорости. Можно сказать, что ускорение есть скорость движения скоростной точки по годографу. Следовательно, все соотношения и теоремы, полученные для скорости, остаются справедливыми и для ускорения, если в них произвести замену величин и терменов согласно следующей таблице:

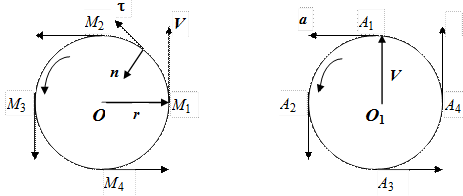
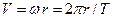
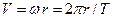
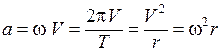
В качестве простейшего примера найдем ускорения точки, равномерно вращающейся по окружности радиуса r (Рис.1.4.а). Скорость V направлена по касательной к окружности, ее величина определяется выражением . Годоргафом будет окружность радиуса V (Рис.1.4.б). Когда материальная точка М вращается по окружности радиуса r, соответствующая ей скоростная точка А вращается в том же направлении по окружности радиуса V, описывая эту окружность за то же время Т. Положениям материальной точки на траектории М₁, М₂, М₃, М₄ соответствуют на годографе положения скоростной точки А₁, А₂, А₃, А₄. Ускорение а направлено по касательной к окружности – годографу и притом к центру О траектории вращающейся точки М. По аналогии с формулой , для величины ускорения можно написать

. (1.12)

(1.12) есть центростремительное ускорение. Ее можно записать в векторной форме

. (1.13)

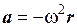
Знак минус указывает на то, что направления векторов а и r взаимно противоположны, т.е. ускорение а направлено к центру круговой траектории, по которой вращается материальная точка. Можно также написать для любого положения движущейся точки

, (1.14)

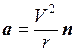
где n – единичный вектор нормали к круговой траектории движущейся точки, направленный к центру О (см. рис.1.4а).

Имея в виду дальнейшие обобщения, представим вектор скорости в виде V= Vt, где t— единичный вектор касательной к окружности. Первый множитель V дает численную величину скорости, второй множитель t указывает ее направление. При равномерном вращении абсолютное значение скорости V остается неизменным, меняется только направление скорости, т. е. единичный вектор t. Дифференцированию подлежит только этот вектор, а потому 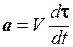. 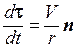Сравнивая это выражение с (1.14), получим

. (1.15)

Формулу (1.15) можно использовать в случе произвольной гладкой кривой. Здесь необходимо ввести два новых понятия: величина 1/r и единичный вектор n. Величина 1/r называется кривизной кривой, r – радиусом кривизны, а n – единичным вектором главной нормали к кривой. При этом кривизна 1/r считается существенно положительной. А потому единичный вектор n всегда направлен сторону вогнутости кривой.

Рассмотрим общий случай движения материальной точки по криволинейной траектории. Запишем вектор скорости в виде V = Vt. Продифференцировав правую и левую часть по времени, получим

, (1.16)

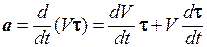
или, с учетом формулы (1.15),

. (1.17)

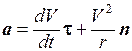
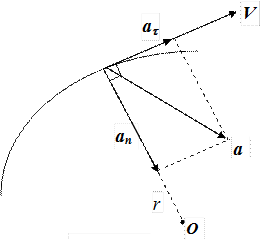
Ускорение а направлено под углом к траектории. Первое слагаемое в формуле (1.17)

(1.18)

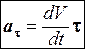
есть вектор, направленный по касательной к траектории. Этот вектор называется касательным или тангенциальным ускорением. Второе слагаемое

(1.19)

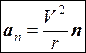
есть вектор, направленный вдоль главной нормали в сторону вогнутости траектории. Он называется нормальным ускорением. Таким образом, в общем случае ускорение а можно представить в виде геометрической суммы тангенциального и нормального ускорения:

. (1.20)

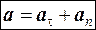
Тангенциальное ускорение меняет скорость только по величине, нормальное ускорение меняет ее только по направлению.

Модуль полного ускорения точки

. (1.21)

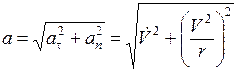
Направления полного ускорения и его составляющих (а_t, а_n) для случая ускоренного движения приведены на рис. 1.5. При замедленном движении вектор а_t имеет противоположное направление.

Характеристика движения материальной точки в зависимости

от тангенциальной и нормальной составляющих ускорения

		Движение
Прямолинейное равномерное
const	Прямолинейное равнопеременное
const	Равномерное по окружности
0	Равномерное криволинейное
const	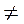0	Криволинейное равнопеременное

Поступательное движение. Это такое движение тела, при котором любая прямая, связанная с телом, все время остается параллельной своему начальному положению. Например, вагон, движущийся по прямому участку пути; кабина колеса обозрения и др.

1. Может ли криволинейное движение быть равномерным?

2. Чему равно скалярное произведение скорости и ускорения в случае равномерного движения по окружности?

3. Что характерно для скоростей и ускорений точек тела, движущегося поступательно?

4. В каких случаях модуль перемещения точки равен длине пути, пройденного точкой за тот же промежуток времени?

5. Как движется точка, если скорость этой точки все время ортогональна ее ускорению?

6. Какова траектория плоского движения точки, если ее радиальная скорость равна нулю?

1. Можно ли утверждать, что точка движется без ускорения в случаях:

а) u = const; б) u= const?

2. Является ли движение точки обязательно прямолинейным в случаях:

а) u= const; б) a= const?

3. Точка движется равномерно по окружности. Начало ее радиус-вектора r совпадает с центром окружности. Отличны ли от нуля выражения dr/dt и dV/dt?

4. При каком движении материальной точки выполняются соотношения a_t = 0, a_n = const ¹ 0: а) при равномерном движении по окружности; б) при равномерном движении по винтовой линии; в) при равномерном прямолинейном движении; г) при равнопеременном движении по окружности?

1) а, б, в; 2) а, б; 3) г; 4) а; 5) а, б, г.

5. Применима ли для вычисления тангенциального ускорения формула a_t = u/t в случаях: а) u= 2t + 6; б) u = 3t 2 ; в) u = 5t (u– в м/с; t – в с)?

6. Математический маятник совершает гармонические колебания. Отличны ли от нуля в крайней точке траектории маятника:

а) нормальное ускорение; б) тангенциальное ускорение?

7. Тело бросили вертикально с некоторой высоты: а) вверх;

б) вниз. Начальные скорости в обоих случаях одинаковы. Сравнить скорости в момент падения тела на землю. Сопротивлением воздуха пренебречь.

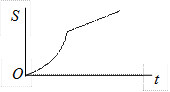
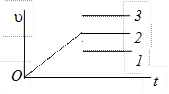
8. Какой график скорости соответствует графику пути на рисунке?

9. Применима ли для вычисления углового ускорения формула e = w/t в случаях: а) w = 2t + 8; б) w = 9t; в) w = 6 (w – в рад/с, t – в с)?

10. Движение тела с неподвижной осью задано уравнением j = 2p(6t – 3t 2 ) (j – в рад, t – в с). Начало движения при t = 0. Сколько оборотов сделает тело до момента изменения направления вращения?

11. Стержень длиной l упирается верхним концом в стену, а нижним – в пол. Конец, упирающийся в стену, равномерно опускается вниз. Будет ли движение другого конца равномерным?

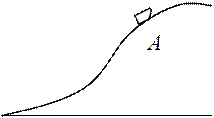
12. У подножия горы санкам сообщена некоторая скорость, в результате чего санки въезжают на гору и, достигнув точки А начинают скользить обратно. Как направлены нормальное и тангенциальное ускорения в точке А.

13. Тело скользит без трения по вогнутой поверхности. Как в наинизшей точке направлены нормальное и тангенциальное ускорения.

Источник

Теоретическая механика:
Кинематика точки

Смотрите также решения задач по теме «Кинематика точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.

* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).

В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.

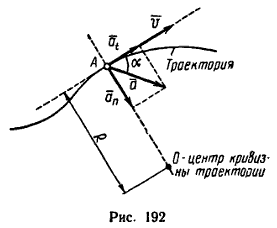
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).

Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.

Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением a_t – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).

Числовое значение касательного ускорения в общем случае определяется по формуле
a_t = dv/dt или a_t = f»(t).

Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением a_n – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).

Числовое значение нормального ускорения определяется в общем случае по формуле
a_n = v 2 /R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.

После того как определены касательное и нормальное ускорения, легко определить и ускорение a ( полное ускорение точки ).

Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(a_t 2 + a_n 2 ).

Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = a_n/a; cos α = a_t/a; tg α = a_n/a_t.

Но можно сначала определить направление полного ускорения a использовав формулу tg α = a_n/a_t,
а затем найти числовое значение a:
a = a_n/sin α или a = a_t/cos α.

Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.

Наличие касательного ускорения (a_t≠0) или его отсутствие (a_t=0) определяют соответственно неравномерность или равномерность движения точки.

Наличие нормального ускорения (a_n≠0) или его отсутствие (a_n=0) определяют криволинейность или прямолинейность движения точки.

Движение точки можно классифицировать так:
а) равномерное прямолинейное (a_t = 0 и a_n = 0);
б) равномерное криволинейное (a_t = 0 и a_n ≠ 0);
в) неравномерное прямолинейное (a_t ≠ 0 и a_n = 0);
г) неравномерное криволинейное (a_t ≠ 0 и a_n ≠ 0).

Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.

Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.

§ 27. Равномерное прямолинейное движение точки

Уравнение равномерного движения имеет вид
(а) s = s₀ + vt
или в частном случае, когда начальное расстояние s₀=0,
(б) s = vt.

В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s₀ и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.

При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.

§ 28. Равномерное криволинейное движение точки

Если a_t = 0 и a_n ≠ 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
a_n = v 2 /R,
где R – радиус кривизны траектории.

В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
a_n = v 2 /r = const.

Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2πr/T = πd/T.

§ 29. Равнопеременное движение точки

Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s₀ + v₀t + a_tt 2 / 2.

Здесь s₀ – расстояние точки от исходного положения в момент начала отсчета; v₀ – начальная скорость и a_t – касательное ускорение – величины численно постоянные, a s и t – переменные.

Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v₀ + a_tt.

Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s₀, v₀, a_t и три переменные: s, v, t.

Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).

Если неизвестные входят в оба основных уравнения, например, неизвестны a_t и t, то для удобства решения таких задач выведены вспомогательные формулы:

после исключения a_t из (1) и (2)
(3) s = s₀ + (v + v₀)t / 2;

В частном случае, когда начальные величины s₀=0 и v₀=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = a_tt 2 / 2;
(6) v = a_tt;
(7) s = vt / 2;
(8) s = v 2 / (2a_t).

Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.

§ 30. Неравномерное движение точки по любой траектории

§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме

Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).

Движение точки в пространстве задается тремя уравнениями:
x = f₁(t);
(1) y = f₂(t);
z = f₃(t);

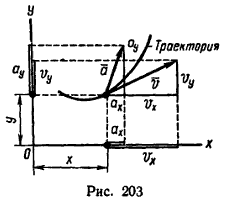
Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f₁(t);
y = f₂(t);

Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).

Если закон движения точки задан в координатной форме, то:

а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;

б) числовое значение скорости точки находится из формулы
v = sqrt(v_x 2 + v_y 2 )
после предварительного определения проекции (см. рис. 203) скорости на оси координат
v_x = dx/dt и v_y = dy/dt;

в) числовое значение ускорения находится из формулы
a = sqrt(a_x 2 + a_y 2 )
после предварительного определения проекций ускорения на оси координат
a_x = dv_x/dt и a_y = dv_y/dt;

г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.

§ 32. Кинематический способ определения радиуса кривизны траектории

При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну ) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
a_n = v 2 /R,
выражающую числовое значение нормального ускорения.

Скорость v точки определяется по формуле
(б) v = sqrt(v_x 2 + v_y 2 ).

Таким образом, если закон движения точки задан уравнениями
x = f₁(t);
y = f₂(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:

1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
v_x = f₁‘(t);
v_y = f₂‘(t).

4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
a_x = f₁»(t) = v_x‘;
a_y = f₂»(t) = v_y‘.

6. Подставить в (в) значения a 2 и a_t 2 и найти a_n.

7. Подставив в (а) найденные значения v 2 и a_n, получить радиус кривизны R.

Источник