Какой параллелепипед называется прямоугольным что такое линейные размеры параллелепипеда

Прямоугольный параллелепипед

Прямоугольный параллелепипед — объёмная фигура, у которой шесть граней, и каждая из них является прямоугольником.

Прямоугольный параллелепипед — параллелепипед, все грани которого являются прямоугольниками.

Примерами прямоугольного параллелепипеда служат классная комната, кирпич, спичечная коробка.

Длины трёх рёбер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями. Например, имеются спичечные коробки с измерениями 15, 35, 50 мм. Формула нахождения объёма прямоугольного параллелепипеда: V=abc

Прямоугольный параллелепипед с равными измерениями называется кубом. Все шесть граней куба — равные квадраты.

Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Ссылки

Полезное

Смотреть что такое «Прямоугольный параллелепипед» в других словарях:

Параллелепипед — (от греч. παράλλος параллельный и греч. επιπεδον плоскость) призма, основанием которо … Википедия

огибающий параллелепипед — 3.12 огибающий параллелепипед (reference box): Воображаемая поверхность, представляющая собой наименьший прямоугольный параллелепипед, который полностью, кроме выступающих частей с незначительным звуковым излучением, заключает в себе испытуемую… … Словарь-справочник терминов нормативно-технической документации

Эйлеров параллелепипед — Рациональный кубоид[1] (или целочисленный кирпич) прямоугольный параллелепипед, у которого все семь основных величин (три ребра, три лицевых диагонали и пространственная диагональ) являются целыми числами. Иначе говоря, рациональный кубоид… … Википедия

ОГИБАЮЩИЙ ПАРАЛЛЕЛЕПИПЕД — воображаемый прямоугольный параллелепипед, полностью вмещающий источник шума, за исключением некоторых, не влияющих на шум выступающих его частей, опирающийся на звукоотражающую плоскость … Российская энциклопедия по охране труда

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

Тетраэдр — (греч. τετραεδρον четырёхгранник) простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Содержание 1 Связанные определения … Википедия

Равногранный тетраэдр — Тетраэдр называется равногранным, если все его грани равные между собой треугольники. Существует ряд эквивалентных определений: описанный около него параллелепипед прямоугольный; его развёртка, полученная при разрезании его по трём… … Википедия

Рациональный кубоид — Рациональный кубоид[1] (или целочисленный кирпич) прямоугольный параллелепипед, у которого все семь основных величин (три ребра, три лицевых диагонали и пространственная диагональ) являются целыми числами. Иначе говоря, рациональный кубоид… … Википедия

Рациональный кирпич — Рациональный кубоид[1] (или целочисленный кирпич) прямоугольный параллелепипед, у которого все семь основных величин (три ребра, три лицевых диагонали и пространственная диагональ) являются целыми числами. Иначе говоря, рациональный кубоид… … Википедия

Целочисленный кирпич — Рациональный кубоид[1] (или целочисленный кирпич) прямоугольный параллелепипед, у которого все семь основных величин (три ребра, три лицевых диагонали и пространственная диагональ) являются целыми числами. Иначе говоря, рациональный кубоид… … Википедия

Источник

Прямоугольный параллелепипед. Что это такое?

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

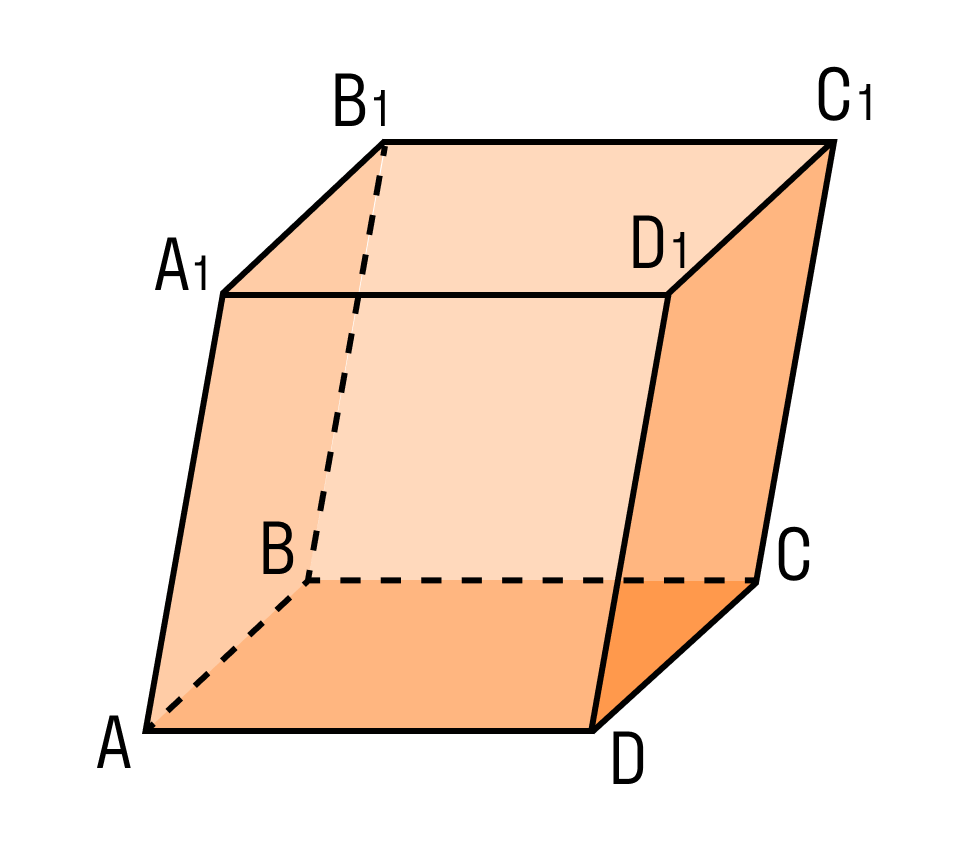
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Формулы прямоугольного параллелепипеда:

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

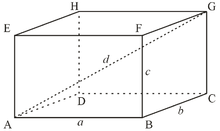
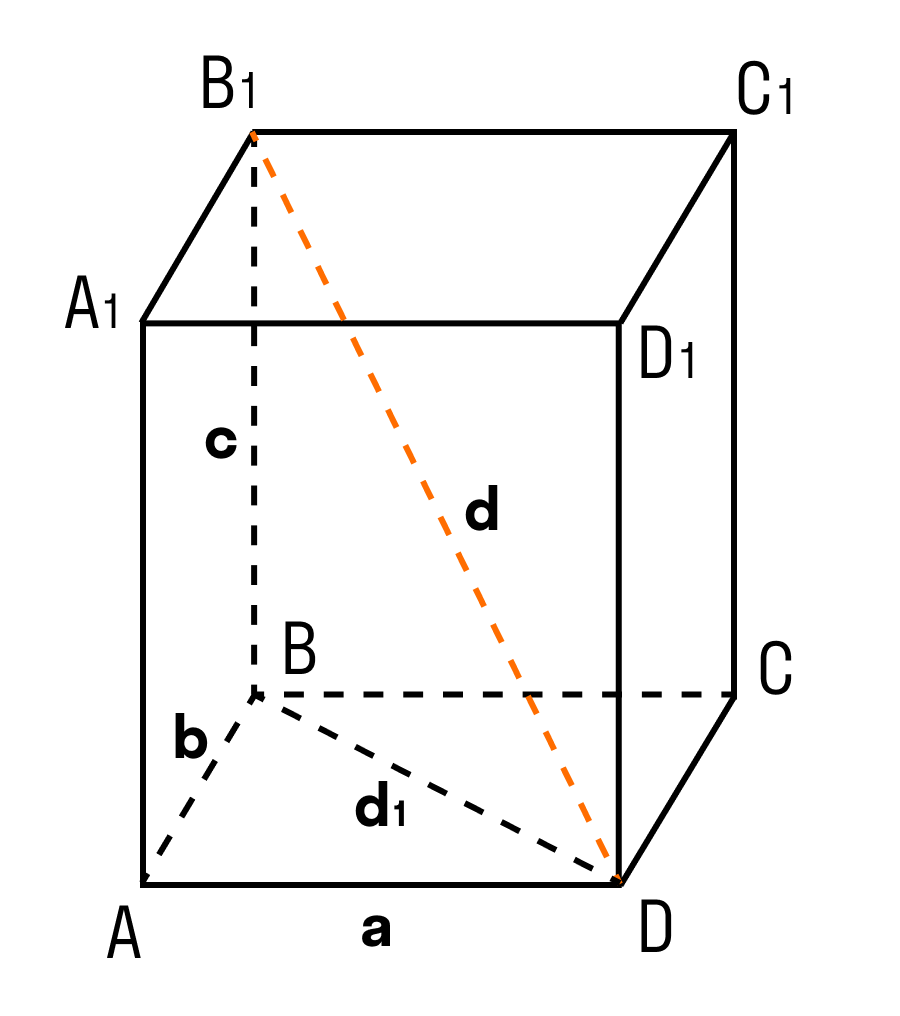
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

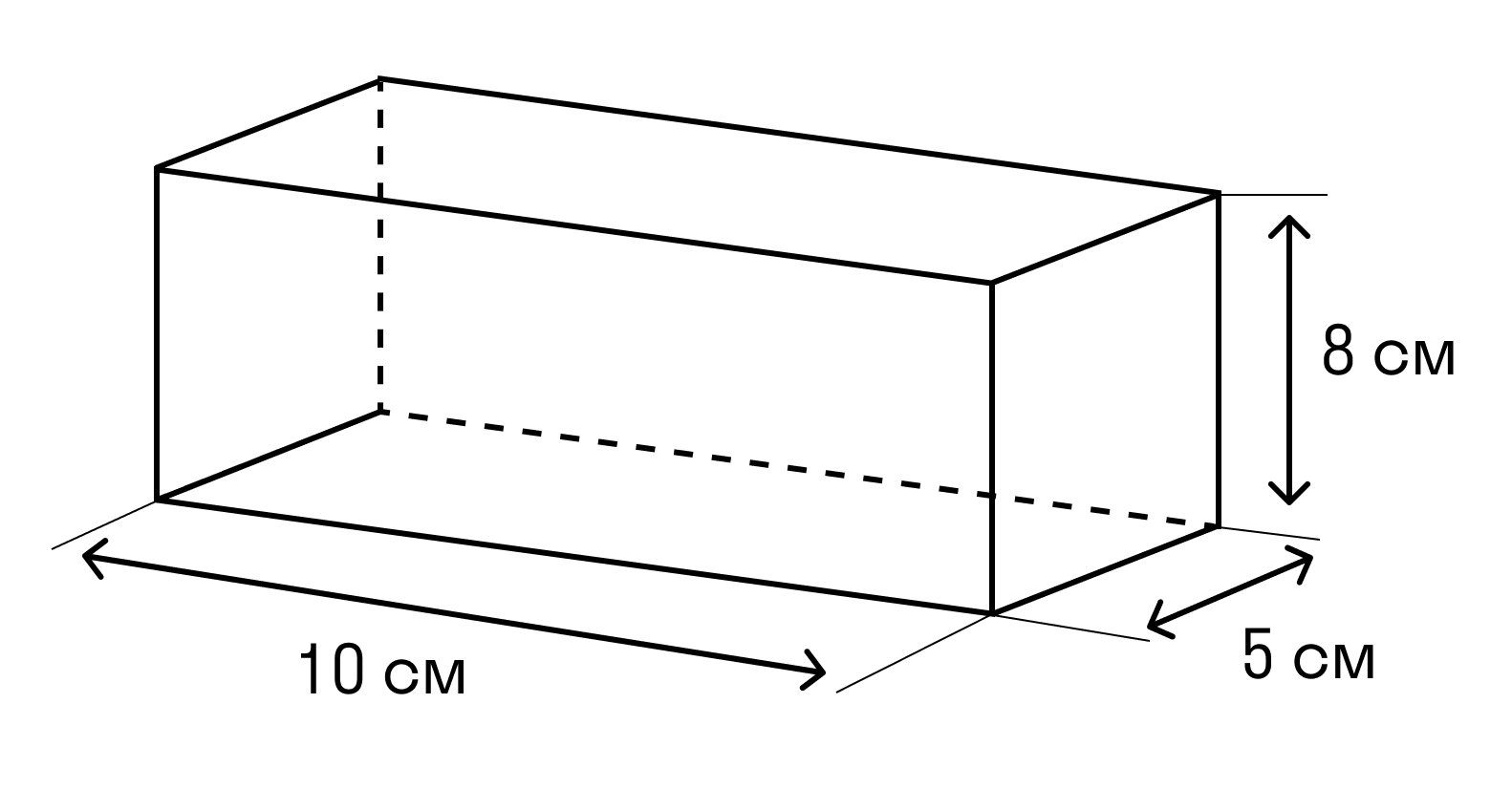
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

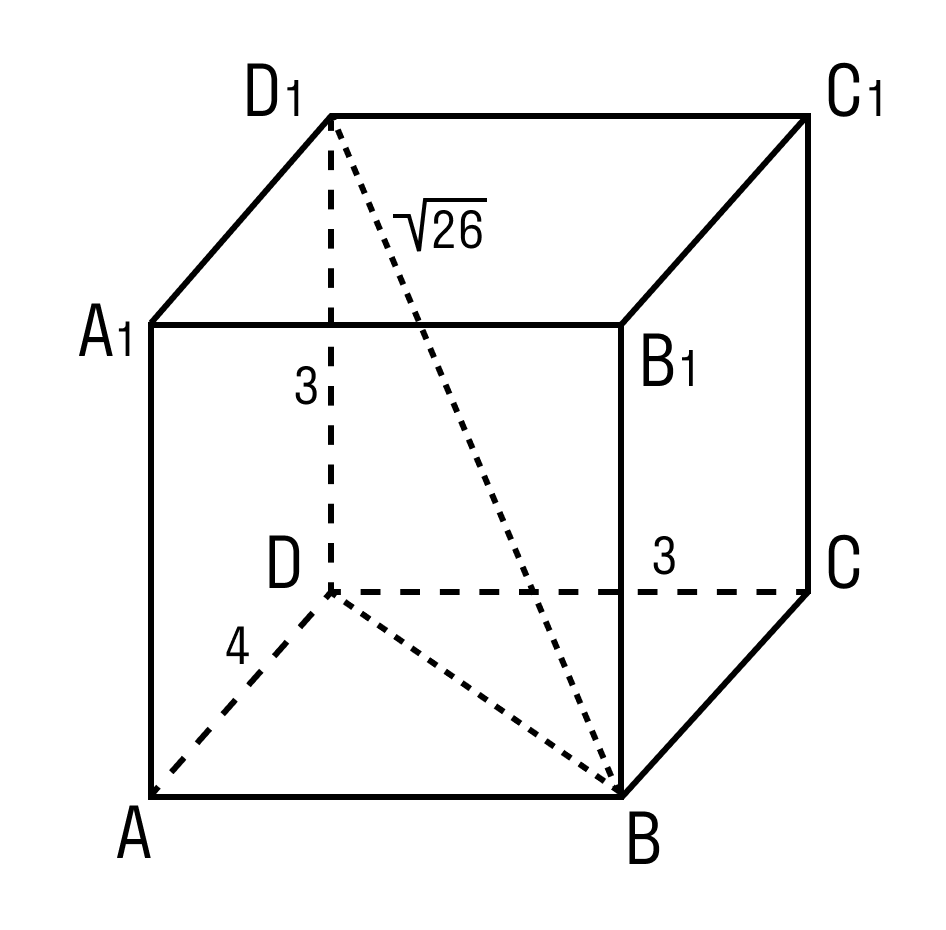
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.

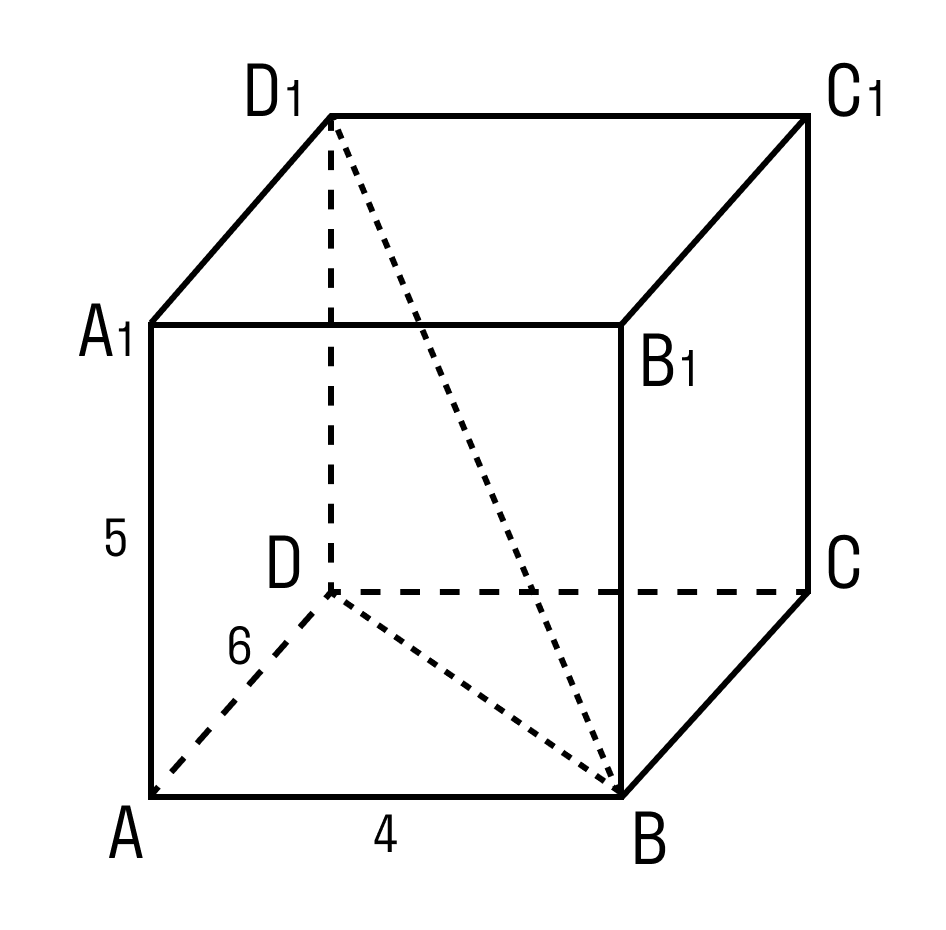
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

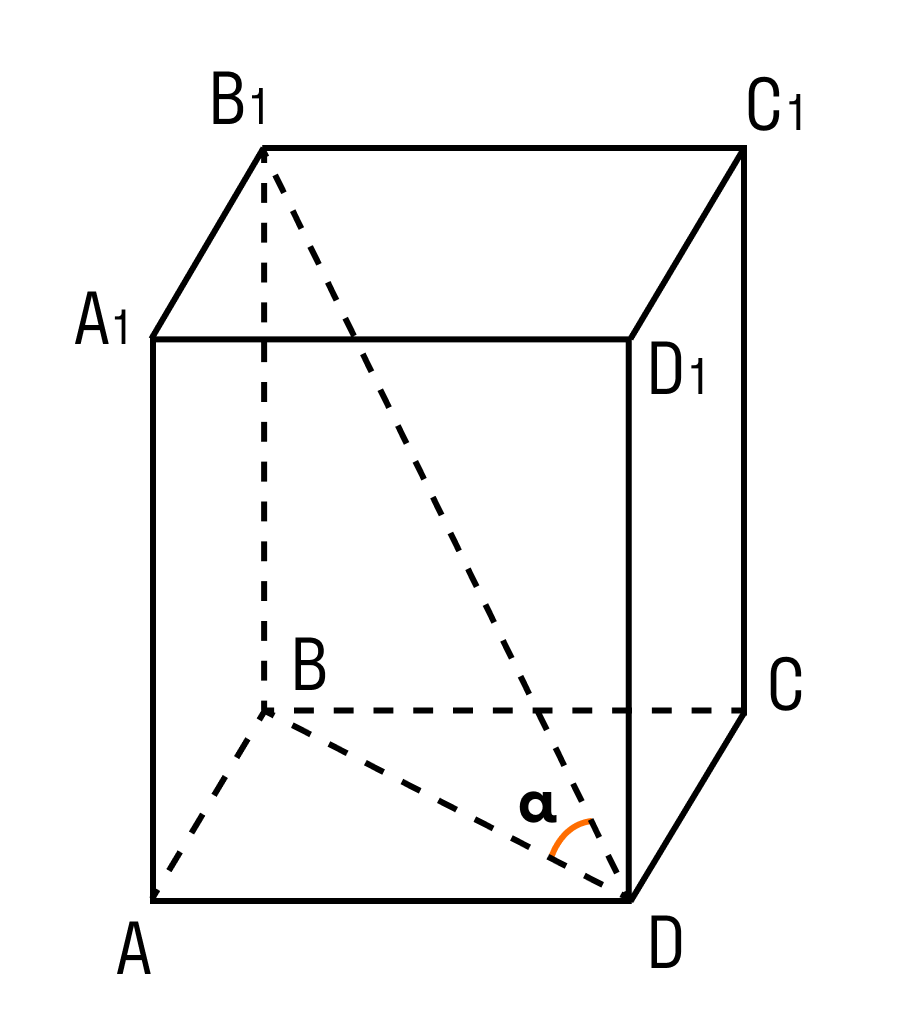
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Источник

Геометрические фигуры. Параллелепипед.

Параллелепипед — призма, основанием которой является параллелограмм либо (равносильно) многогранник с шестью гранями, являющимися параллелограммами. Шестигранник.

Параллелограммы, из которых состоит параллелепипед являются гранями этого параллелепипеда, стороны этих параллелограммов являются ребрами параллелепипеда, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда каждая грань является параллелограммом.

Как правило выделяют любые 2-е противолежащие грани и называют их основаниями параллелепипеда, а оставшиеся грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, которые не принадлежат основаниям являются боковыми ребрами.

2 грани параллелепипеда, которые имеют общее ребро являются смежными, а те, которые не имеют общих ребер — противоположными.

Отрезок, который соединяет 2 вершины, которые не принадлежат 1-ой грани является диагональю параллелепипеда.

Длины ребер прямоугольного параллелепипеда, которые не параллельны, являются линейными размерами (измерениями) параллелепипеда. У прямоугольного параллелепипеда 3 линейных размера.

Типы параллелепипеда.

Существует несколько видов параллелепипедов:

Прямым является параллелепипед с ребром, перпендикулярным плоскости основания.

Прямой параллелепипед с прямоугольником в основании является прямоугольным параллелепипедом. У прямоугольного параллелепипеда каждая из граней является прямоугольником.

Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, по отношению к основаниям, под углом, не равным 90 градусов.

Прямоугольный параллелепипед, у которого все 3 измерения имеют равную величину, является кубом. Каждая из граней куба – это равные квадраты.

Произвольный параллелепипед. Объём и соотношения в наклонном параллелепипеде в основном определяются при помощи векторной алгебры. Объём параллелепипеда равняется абсолютной величине смешанного произведения 3-х векторов, которые определяются 3-мя сторонами параллелепипеда (которые исходят из одной вершины). Соотношение между длинами сторон параллелепипеда и углами между ними показывает утверждение, что определитель Грама данных 3-х векторов равняется квадрату их смешанного произведения.

Свойства параллелепипеда.

В параллелепипед вписывают тетраэдр. Объем этого тетраэдра будет равняться третьей части объема параллелепипеда.

Источник

Математика. 5 класс

Конспект урока

Перечень рассматриваемых вопросов:

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.

Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью.

Основания параллелепипеда – это его верхняя и нижняя грани.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 класс. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Мир, в котором мы живём, состоит из огромного количества разных по форме, цвету и размеру предметов. Изучая их свойства, люди открывают что-то новое. Например, математики в окружающем пространстве обращают внимание на геометрические тела: цилиндры, кубы и так далее.

Сегодня мы рассмотрим прямоугольный параллелепипед – многогранник, название которого с древнегреческого переводится как «идущие рядом плоскости».

Прямоугольный параллелепипед ограничен шестью прямоугольниками, то есть шестью гранями. Грань, на которую поставлен параллелепипед, и ей противоположную называют нижним и верхним основаниями.

Остальные четыре грани называют боковыми гранями.

Стороны граней параллелепипеда называют рёбрами. Их двенадцать.

Концы рёбер называют вершинами. Их в параллелепипеде восемь.

Каждая вершина является общим концом трёх рёбер.

Длины двух рёбер основания, выходящих из одной вершины, называют длиной и шириной прямоугольного параллелепипеда.

Длину бокового ребра называют высотой.

Таким образом, длины трёх рёбер, выходящих из одной вершины, называют длиной, шириной, высотой. Иначе длину, ширину и высоту называют измерениями прямоугольного параллелепипеда.

Прямоугольный параллелепипед, у которого три ребра, выходящие из одной вершины, равны между собой, называется кубом. Каждая грань куба – квадрат.

Рассмотрим свойства прямоугольного параллелепипеда и куба.

У прямоугольного параллелепипеда противоположные грани равны.

Все грани куба равны между собой.

Построим прямоугольник заданной длины а и высоты h.

Для этого от каждой вершины отложим отрезок, равный половине ширины b под углом 45 градусов. И соединим концы отрезков, причём невидимые грани – пунктирной линией.

Изготовить параллелепипед можно несколькими способами. Например, с помощью развёртки. Для этого на бумаге вычерчивается макет, который выглядит как приведённый шаблон. Обратите внимание, что на картинке даны припуски для того, чтобы можно было склеить параллелепипед.

Другой способ изготовления параллелепипеда – модульная сборка. Она требует ряда последовательных действий.

1) Вырежьте из бумаги шесть одинаковых квадратов.

2) Согните их к середине, как показано на картинке.

3) Согните верхние и нижние края заготовки, как показано на рисунке.

4) Верхний уголок опустите вниз, а нижний – загните наверх. После этого получится квадрат.

5) Сделайте шесть таких заготовок и соедините их в один параллелепипед. Для этого каждый острый уголок вставьте в кармашек соседней части кубика.

№ 1. Какова площадь верхней грани параллелепипеда?

Решение: площадь верхней грани параллелепипеда соответствует площади прямоугольника. Верхняя грань параллелепипеда имеет длину 15см и ширину 3см. Значит, далее по формуле вычисляем площадь:

S = а ·b = 15 см · 3 см = 45 см 2

Ответ: 45 см 2

№ 2. На рисунке изображен куб, состоящий из нескольких маленьких кубиков. Сколько маленьких кубиков ушло на построение данного куба?

Решение: для решения задачи нужно посмотреть, сколько маленьких кубиков расположено на одной грани куба. Их 9 штук. Всего на рисунке изображено три грани. Таким образом, чтобы найти общее количество маленьких кубиков, следует умножить количество кубиков, умещающихся на одной грани, на количество граней: 9 · 3= 27 штук.

Источник

Параллелепипед

Параллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.

Содержание

Типы параллелепипеда

Различается несколько типов параллелепипедов:

Основные элементы

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Свойства

Основные формулы

Прямой параллелепипед

Площадь боковой поверхности S_б=Р_о*h, где Р_о — периметр основания, h — высота

Площадь полной поверхности S_п=S_б+2S_о, где S_о — площадь основания

Прямоугольный параллелепипед

Площадь боковой поверхности S_б=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда

Площадь полной поверхности S_п=2(ab+bc+ac)

Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

Площадь боковой поверхности S_б=4a², где а — ребро куба

Площадь полной поверхности S_п=6a²

Произвольный параллелепипед

В математическом анализе

В математическом анализе под n-мерным прямоугольным параллелепипедом понимают множество точек вида

Примечания

Ссылки

Полезное

Смотреть что такое «Параллелепипед» в других словарях:

ПАРАЛЛЕЛЕПИПЕД — греч., от parallelos., параллельный, и epidon, поверхность. Четырехсторонняя призма, у которой противоположные стороны параллельны между собой. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней.… … Словарь иностранных слов русского языка

Параллелепипед — Параллелепипед. ПАРАЛЛЕЛЕПИПЕД (от греческого parallelos параллельный и epipedon плоскость), призма, основание которой параллелограмм. … Иллюстрированный энциклопедический словарь

параллелепипед — призма, ромбоэдр, шестигранник Словарь русских синонимов. параллелепипед сущ., кол во синонимов: 4 • многогранник (38) • … Словарь синонимов

ПАРАЛЛЕЛЕПИПЕД — (от греч. parallelos параллельный и epipedon плоскость) призма, основанием которой служит параллелограмм … Большой Энциклопедический словарь

ПАРАЛЛЕЛЕПИПЕД — ПАРАЛЛЕЛЕПИПЕД, параллелепипеда, муж. (от греч. parallelos параллельный и epipedon поверхность) (мат.). Шестигранник, у которого противоположные грани равны и параллельны. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

ПАРАЛЛЕЛЕПИПЕД — ПАРАЛЛЕЛЕПИПЕД, а, муж. В математике: призма, основанием к рой служит параллелограмм. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

Параллелепипед — шестигранник, каждая пара противоположных гранейкоторого суть параллелограммы равной величины и параллельные междусобой … Энциклопедия Брокгауза и Ефрона

параллелепипед — а, м. parallélépipède m. <гр. parallelos + epidepon плоскость. геом. Шестигранник, сторонами которого являются параллелограммы. Крысин 1998. Цвет его <сапфира> лазуревой, сложение листоватое; представляет шести или многоугольную призьму … Исторический словарь галлицизмов русского языка

ПАРАЛЛЕЛЕПИПЕД — призма, основанием которой является (см.) … Большая политехническая энциклопедия

Параллелепипед — (греч. parallelepípedon, от parállelos параллельный и epípedon плоскость) шестигранник, противоположные грани которого попарно параллельны. П. имеет 8 вершин, 12 рёбер; его грани представляют собой попарно равные параллелограммы. П.… … Большая советская энциклопедия

Источник

• ← Какой падеж отвечает на вопросы на чем
• Какой пароль чего пароль →

Многогранники
Правильные (Платоновы тела)	Трёхмерные Правильный тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр Четырёхмерные 6 правильных многогранников Большей размерности N-мерный куб • N-мерный октаэдр • N-мерный тетраэдр
Звёздчатый додекаэдр • Звёздчатый икосододекаэдр • Звёздчатый икосаэдр • Звёздчатый многогранник • Звёздчатый октаэдр
Выпуклые	Архимедовы тела Кубооктаэдр • Икосододекаэдр • Усечённый тетраэдр • Усечённый октаэдр • Усечённый икосаэдр • Усечённый куб • Усечённый додекаэдр • Ромбокубоктаэдр • Ромбоикосододекаэдр • Ромбоусечённый кубоктаэдр • Ромбоусечённый икосододекаэдр • Курносый куб • Курносый додекаэдр • Усечённый кубооктаэдр • Усечённый икосододекаэдр • Правильная призма • Антипризма Каталановы тела Ромбододекаэдр • Ромботриаконтаэдр • Триакистетраэдр • Тетракисгексаэдр • Пентакисдодекаэдр • Триакисоктаэдр • Триакисикосаэдр • Дельтоидальный икоситетраэдр • Дельтоидальный гексеконтаэдр •Пентагональный икоситетраэдр • Пентагональный гексеконтаэдр • Дисдакисдодекаэдр • Дисдакистриаконтаэдр Без полной пространственной симметрии Пирамида • Призма • Бипирамида • Антипризма • Зоноэдр • Параллелепипед • Ромбоэдр •Призматоид• Усечённая пирамида• Пентагондодекаэдр • Параллелоэдр
Формулы, теоремы, теории