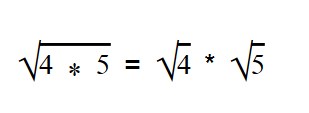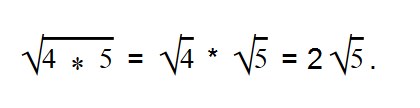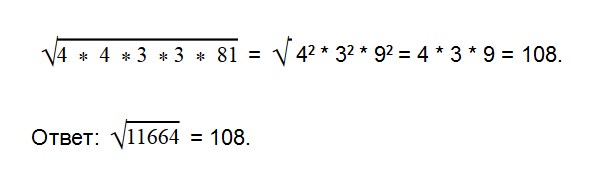Квадратный корень что это в математике

Что такое квадратный корень

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

Это два нетождественных друг другу выражения.

Из выражения x 2 = 16 следует, что:

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

Ищем в таблице число 7396.

Ищем в таблице число 9025.

Ищем в таблице число 1600.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

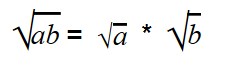Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

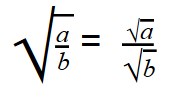Примеры:

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

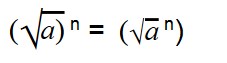Примеры:

Эти две формулы нужно запомнить:

Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10

Источник

Корень и его свойства

Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.

Определение «Корень»

Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √ 64 = 8 (√ 64 равно числу 8).

Формула: √ a 2 = a

Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.

Извлечение корней: примеры

Найти корень из числа можно одним из следующих способов:

Приведение корней с разными показателями

Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.

Например, есть квадратный корень (второй степени √ 2 ) и кубический корень (третьей степени 3 √ 3 ).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n √ a n : √ 2 = 2 √ 2 = 6 √ 2 3 = 6 √ 8 ; 3 √ 3 = 6 √ 3 2 = 6 √ 9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.

Корень: сложение и вычитание корней

Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.

Примеры:
2√ 3 + 3√ 3 = 5√ 3
2√ 3 + 2√ 4 – не выполняется.

Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!

Корень: умножение

Умножение корней без множителей

Произведение корней из чисел равно корню из произведения этих чисел.
√ a*b =√ a *√ b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√ 2 х √ 3 = √ 6
√ 6 х √ 3 = √ 18 = √ 3х3х2 = 3√ 2

Умножение корней с множителями

При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√ 2 х √ 5 = (3х1) √ (2*5) = 3√ 10
4√ 2 х 3√ 3 = (3х4) √ (2х3) = 12√ 6

Корень: деление

Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√ a:b =√ a :√ b
В процессе деления квадратных корней дроби упрощаются.

Деление корней без множителей

Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √ 21 :√ 3 =√ 21:3 =√ 7

Деление квадратных корней с множителями

Примеры для практики

Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«

Источник

Свойства корней (ОГЭ, ЕГЭ 2022)

А сейчас мы рассмотрим свойства корней.

Квадратный корень, кубический корень и корень в N-ой степени.

Порешаем задачки, чтобы к концу этого занятия все, что касается корней (в любой степени) было тебе абсолютно понятно!

И, самое главное, чтобы ты смог решить любую задачу c корнями на экзамене!Поехали!

Свойства корней — коротко о главном

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)

Свойства корней:

Для любого натурального \( n\), целого \( k\) и любых неотрицательных чисел \( a\) и \( b\) выполнены равенства:

Арифметический квадратный корень

Когда ты разберешься в этой теме, тебе станет намного легче решать иррациональные уравнения и неравенства.

А пока что давай попробуем разобраться, что это за понятие «корень» и с чем его едят 🙂

Для этого рассмотрим примеры, с которыми ты уже сталкивался на уроках (ну, или тебе с этим только предстоит столкнуться).

К примеру, перед нами уравнение \( <^<2>>=4\). Какое решение у данного уравнения? Какие числа можно возвести в квадрат и получить при этом \( 4\)?

Для упрощения, математики ввели специальное понятие квадратного корня и присвоили ему специальный символ \( \sqrt<\ \ >\).

Дадим определение арифметическому квадратному корню.

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)
\( \left( \sqrt=x,\ <^<2>>=a;\ \ x,a\ge 0 \right)\)

А почему же число \( a\) должно быть обязательно неотрицательным?

Например, чему равен \( \sqrt<-9>\). Так-так, попробуем подобрать. Может, три?

Это надо запомнить: число или выражение под знаком корня должно быть неотрицательным!

Однако самые внимательные уже наверняка заметили, что в определении сказано, что решение квадратного корня из «числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)».

Такое замечание вполне уместно. Здесь необходимо просто разграничить понятия квадратных уравнений и арифметического квадратного корня из числа.

Квадратное уравнение или квадратный корень?

К примеру, \( <^<2>>=4\) не равносильно выражению \( x=\sqrt<4>\).

Из \( <^<2>>=4\) следует, что \( \left| x \right|=\sqrt<4>\), то есть \( x=\pm \sqrt<4>=\pm 2\) или \( <_<1>>=2;\ <_<2>>=-2\).

А из \( x=\sqrt<4>\) следует, что \( x=2\).

Конечно, это очень путает, но это необходимо запомнить, что знаки являются результатом решения уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.

А теперь попробуй решить такое уравнение \( <^<2>>=3\).

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля: \( <<0>^<2>>=0\) – не подходит.

Двигаемся дальше \( \text=1;\ <<1>^<2>>=1\) – меньше трех, тоже отметаем.

А что если \( x=2\); \( <<2>^<2>>=4\) – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными. И что дальше?

Давай построим график функции \( y=<^<2>>\) и отметим на нем решения. (Прочти по ссылке как использовать график функции для решения уравнений)

Давай попробуем обмануть систему и получить ответ с помощью калькулятора! Извлечем корень из \( 3\), делов-то! Ой-ой-ой, выходит, что \( \sqrt<3>=1,732050807568…\).

Такое число никогда не кончается.

Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.

Рассмотрим еще один пример для закрепления.

Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной \( \displaystyle 1\) км, сколько км тебе предстоит пройти?

Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора: \( <^<2>>=<^<2>>+<^<2>>\). Таким образом, \( <^<2>>=1+1=2\).

Так чему же здесь равно искомое расстояние?

Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать. Для этого необходимо знать, по меньшей мере, квадраты чисел от \( 1\) до \( 20\), а также уметь их распознать.

К примеру, необходимо знать, что \( 15\) в квадрате равно \( 225\), а также, наоборот, что \( 225\) – это \( 15\) в квадрате.

Вот тебе полная таблица квадратов чисел. Сверху строка — основание степени, слева в столбик показатель степени, на пересечение искомое значение степени. Запомнить нужно только то, что выделено зеленым.

Уловил, что такое квадратный корень? Тогда порешай несколько примеров.

Источник

Арифметический корень.

Длина стороны квадрата не может быть отрицательным числом, поэтому искомая стороны квадрата 3 см.

Корнем n -й степени из числа α является такое число b, где b n = α.

Здесь n—натуральное число принято называть показателем корня (или степенью корня); как правило, оно больше или равно 2, потому что случай n = 1 банально.

Мы получили положительное и отрицательное значение корня. Эта особенность усложняет расчеты. Чтобы добиться однозначность, было введено понятие арифметического корня, значение которого всегда со знаком плюс, то есть только положительное.

Корень называется арифметическим, если он извлекается из положительного числа и сам является положительным числом.

Арифметический корень заданной степени из заданного числа существует только один.

Операцию расчетов принято называть «извлечением корня n-й степени» из числа α. По сути мы выполняем операцию обратную к возведению в степень, а именно — нахождение основания степени b по известному показателю n и результату возведения в степень

Корни второй и третьей степени используются на практике чаще остальных и поэтому им были даны специальные названия.

Квадратный корень: В этом случае показатель степени 2 принято не писать, а термин «корень» без указания степени чаще всего означает квадратный корень. Геометрически толкование, является длина стороны квадрата, площадь которого равна α.

Кубический корень: Геометрически толкованием, выступает длина ребра куба, объём которого равен α.

Свойства арифметических корней.

1) При вычислении арифметического корня из произведения, необходимо извлечь его из каждого сомножителя отдельно

2) Для расчета корня из дроби, необходимо извлечь его из числителя и знаменателя данной дроби

3) При расчете корня из степени, необходимо разделить показатель степени на показатель корня

Первые расчеты, связанные с извлечением квадратного корня, обнаружены в работах математиков древнего Вавилона и Китая, Индии, Греции (о достижениях древнего Египта в этом отношении в источниках информация отсутствует).

Математики древнего Вавилона (II тысячелетие до н. э.) применяли для извлечения квадратного корня особый численный метод. Начальное приближение для квадратного корня находили исходя из ближайшего к корню (в меньшую сторону) натурального числа n. Представив подкоренное выражение в виде: α=n 2 +r, получаем: x₀=n+r/2n, затем применялся итеративный процесс уточнения:

Итерации в этом методе очень быстро сходятся. Для ,

Например, α=5; n=2; r=1; x₀=9/4=2,25 и мы получаем последовательность приближений:

В заключительном значении верны все цифры, кроме последней.

Греки сформулировали проблему удвоения куба, которая сводилась к построению кубического корня с помощью циркуля и линейки. Правила вычисления любой степени из целого числа, изучены математиками Индии и арабских государств. Далее они получили широкое развитие в средневековой Европе.

Сегодня для удобства расчетов квадратных и кубических корней широко используются калькуляторы.

Источник