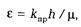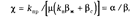Пьезопроводность пласта в чем измеряется

Коэффициент пьезопроводности

Коэффициент проводимости

Коэффициент гидропроводности

где k_пр — проницаемость пласта в районе исследуемой скважины; h — работающая толщина пласта; m — вязкость жидкости или газа. Размерность коэффициента м 5 /(Н×с). Коэффициент e — наиболее емкая характеристика продуктивного пласта, определяющая его производительность в скважине.

a= k_пр/m

Размерность коэффициента м 4 /(Н×с): он характеризует подвижность флюида в пластовых условиях в районе скважины.

Значения параметров пласта, необходимые для получения комплексных характеристик указанным путем, получают другими независимыми методами. Коэффициент проницаемости и комплексные характеристики пласта можно определить с помощью других гидрогазодинамических методов исследования скважин и пластов

Источник

Фильтрационно-емкостные и упругие свойства пластов

На процесс фильтрации оказывают влияние свойства, как коллектора, так и движущейся по нему жидкости. Общепринято характеризовать однородный изотропный пласт толщиной , пористостью , проницаемостью сжимаемостью , водонасыщенностью .

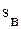
В свою очередь, пластовая жидкость, заполняющая поры коллектора, характеризуется плотностью , вязкостью , сжимаемостью , и напряжением сдвига . С учетом условий залеганий и эксплуатации месторождения, перечисленные выше характеристики, сами могут быть функциями давления и температуры.

Перечисленные выше фильтрационные параметры пласта и жидкости представлены, рис.4.1, где показаны общеупотребительные комбинации между ними, характеризующие среду в целом и определяемые непосредственно гидродинамическими методами исследований.

Вначале рассмотрим комплексные параметры, далее – отдельные их составляющие.

Коэффициент гидропроводности

Величина коэффициента гидропроводности пласта определяет фильтрационно-емкостные свойства пласта и вычисляется по формуле:

, (4.1)

здесь 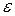– коэффициент гидропроводности, мкм 2 ×см/мПа×с.

Коэффициент определяется непосредственно при исследовании скважин методом снятия кривой восстановления или падения давления. По величине этого параметра можно сравнивать характеристики различных продуктивных пластов. Чем выше гидропроводность, тем при прочих равных условиях будут более высокие дебиты.

Иногда для проведения некоторых расчетов вычисляют производные от коэффициента гидропроводности:

– коэффициент подвижности , мкм 2 /мПа×с

– коэффициент проводимости , мкм 2 ×см.

Коэффициент пьезопроводности

Коэффициент пьезопроводности пласта характеризует его способность к передаче возмущений (изменений давления) по пласту, вызываемых изменениями режима эксплуатации скважин.

Чем больше величина , тем быстрее передается импульс давления по пласту от возмущающей скважины к реагирующей. Для однородного пласта величина определяется расчетным путем из выражения:

1. Для нефтяных залежей

, (4.2)

2. Для газовых залежей

, (4.3)

где – коэффициенты сжимаемости жидкости и пласта, 1/МПа;

– эффективная пористость, д.е.;

– вязкость жидкости и газов при пластовом давлении, мПа·с;

– пластовое давление, МПа.

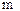
Коэффициент относительной пьезопроводности.

Определяется отношением вида , по результатам исследования скважин методом восстановления давления. Входящий в этот компонент параметр это приведенный радиус скважиныхарактеризует степень вскрытия пласта и состояние призабойной зоны скважины. Определив по результатам гидропрослушивания или, например, расчетным методом, можно оценить приведенный радиус скважины .

Коэффициент емкости пласта

Коэффициент емкости пласта на единицу площади вычисляется по формуле:

, (4.4).

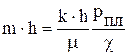
Коэффициент продуктивности

Коэффициент продуктивности определяет добывные возможности скважины при снижении забойного давления на 1 МПа. Согласно уравнению Дюпюи для радиального притока жидкости коэффициент продуктивности скважины:

, (4.5)

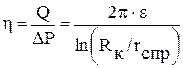
где 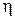– коэффициент продуктивности, м 3 /сут·МПа.

Коэффициент продуктивности – комплексный параметр, имеющий физическую размерность, общую с размерностью гидропроводности , включает в себя дополнительное влияние геометрических размеров скважины , дренируемый радиус пласта , то есть большое количество факторов, влияющих на производительность скважины. Вышеизложенное подтверждает, что гидродинамические методы исследований, в основном, определяют только комбинации параметров и не дают прямых методов их определения.

Если возникает необходимость выделить какой-либо отдельный параметр из комплекса, например, проницаемость из гидропроводности или продуктивности, необходимо иметь дополнительные сведения, характеризующие емкостные, коллекторские и упругие свойства пласта, а также физико-химические и термодинамические свойства жидкостей и газов, насыщающих пласт.

Пористость

Емкостные свойства характеризуются так называемой пористостью (коэффициентом пористости). Различают абсолютную и эффективную пористость.

Абсолютной пористостью называется отношение суммарного объема пор к полному объему породы :

, (4.6)

здесь – абсолютная пористость.

Отношение объема открытых пор к объему всей породы называется открытой (эффективной) пористостью :

. (4.7)

При решении многих задач разработки нефтяных и газовых месторождений используется характеристика, называемая динамическойпористостью коллектора . Эта величина определяется как отношение объема пор породы , по которым жидкость или газ способны двигаться, к объему всей породы :

. (4.8)

Динамическая пористость определяется удельным объемом пор, которые осваиваются текущей жидкостью: нефтью и следующей за ней водой. Динамическая пористость может быть много меньше открытой, вследствие чего скорость движения меченых частиц достигает 5‑6 км/сут, а каналы жидкости образуют ручейки, разбивающие поровое пространство на нефтенасыщенные “островки”, блоки, из которых нефть постепенно попадает в ручейки под действием капиллярных сил.

Проницаемость

Под проницаемостью понимается способность коллектора пропускать жидкость или газ. Различают понятияабсолютной, фазовой и относительной проницаемости.

Абсолютная проницаемость определяет фильтрационную характеристику пористой среды и остается постоянной независимо от движения по пласту воды, нефти и газа. Абсолютная проницаемость определяется в основном в лабораторных условиях по керну (газо- или воздухопроницаемость).

Фазовой (эффективной) проницаемостью называется проницаемость пласта для данной фазы при движении в порах многофазных смесей (смеси нефти, воды и газа или нефти и воды) .

Отношение фазовой проницаемости к абсолютной называется относительной проницаемостью данной фазы:

. (4.9)

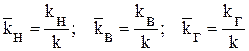
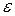
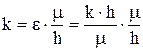
Проницаемость, определяемая по данным гидродинамических исследований, является в основном фазовой. Она определяется расчетным путем по коэффициенту гидропроводности пласта , полученной путем обработки результатов исследований методом неустановившихся режимов фильтрации:

, (4.10)

или по методу установившихся отборов:

, (4.11)

где h – коэффициент продуктивности скважины;

m – вязкость нефти, (воды или смеси воды и нефти);

– работающая толщина пласта;

– объемный коэффициент нефти (смеси);

– функция, зависящая от системы разработки, геометрических размеров скважины и качества вскрытия пласта.

Источник

Добыча нефти и газа

Изучаем тонкости нефтегазового дела ВМЕСТЕ!

Понятия об упругом режиме пласта

Упругий режим характеризуется двумя особенностями:

* неустановившимися процессами перераспределения давления в пласте;

* изменением упругого запаса жидкости в пласте.

При упругом режиме движение возникает в призабойной зоне в начале эксплуатации скважины за счет использования потенциальной энергии упругой деформации пласта и жидкости и только через некоторое время оно распространяется на более отдалённые области.

При снижении пластового давления объём сжатой жидкости увеличивается, а объём порового пространства сокращается за счет расширения материала пласта. Всё это способствует вытеснению жидкости из пласта в скважину.

В ряде случаев приток жидкости поддерживается за счет напора воды, поступающей извне. Такой режим называется упруговодонапорным.

Если залежи нефти ограничены либо зонами выклинивания, либо экранами, то режим называется замкнуто-упругим. В начальной стадии разработки такой залежи до тех пор, пока пластовое давление не снизилось ниже давления насыщения, имеет место замкнуто-упругий режим фильтрации.

Если вытеснение жидкости из пласта происходит не под действием преобладающего влияния упругости пласта и жидкости, то упруговодонапорный режим переходит в жестко-водонапорный режим. При этом режиме влияние упругости пласта и жидкости на фильтрационный поток хотя и не прекращается, но заметно не проявляется.

Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта k, и тем медленнее, чем больше вязкость жидкости m и коэффициенты объёмной упругости жидкости и пласта.

4.1.2. Основные параметры теории упругого режима

Важнейшими параметрами теории упругого режима являются коэффициенты объёмной упругости жидкости и пласта.

Коэффициент объёмной упругости жидкости bж характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объёма изменяется объём жидкости при изменении давления на единицу

, (4.1)

Коэффициент объёмной упругости пласта определяется по формуле

, (4.2)

Dtз = bжt0жDр + bсt0Dр, (4.3)

Так как t0ж = mt0, то

Вскрытие пласта и изменение режима работы скважины вызывает возмущение в пласте. От источника возмущения оно передаётся во все стороны пласта с какой-то скоростью. Скорость распространения изменения пластового давления характеризуется коэффициентом пьезопроводности пласта

. (4.5)

Здесь L, T –размерности длины и времени.

В коллекторах – 1000см2/с £ k £ 50000см2/c или 0.1м2/с £k £5м2/c.

Степень нестационарности процессов определяется безразмерными параметрами Фурье:

для всего пласта , (4.7)

4.1.3. Дифференциальное уравнение неустановившейся фильтрации упругой жидкости (уравнение пьезопроводности)

Считаем, что течение происходит по закону Дарси, и уравнение состояния упругой жидкости в линеаризованной постановке, которое получим из соотношения (2.27) разложением экспоненты в ряд Тейлора, имеет вид

, (4.8)

а также изменение пористости в зависимости от давления, полученное линеаризацией соотношения (2.34), описывается зависимостью

. (4.9)

Из (4.9) и очевидного соотношения имеем следующее дифференциальное уравнение для пористости, при пренебрежении членом, содержащим произведение bжbс

. (4.10)

В то же время из общего уравнения фильтрации (2.8) .

Приравнивая правые части, с учетом выражения для потенциала , и пренебрегая членом, содержащим (р-р0)2, получим

. (4.11)

Уравнение типа (4.11) известно под названием уравнения теплопроводности, а в теории фильтрации называется уравнением пьезопроводности. По аналогии с уравнением теплопроводности коэффициент k характеризует быстроту распределения давления в пласте и носит название коэффициент пьезопроводности. Само уравнение (4.11) позволяет определить поле давления при нестационарных процессах в пласте с упругим режимом.

4.1.4. Приток к скважине в пласте неограниченных размеров

4.1.4.1. Вывод основного уравнения упругого режима

Считаем пласт упругим, горизонтальным и большой протяженности и в нём имеется одна скважина, тогда движение жидкости в пласте можно считать плоскорадиальным к точечному стоку (эксплуатационная скважина) или от точечного источника (нагнетательная скважина).

Рассмотрим процесс перераспределения давления при неустановившемся, плоском радиальном движении жидкости. Для этого запишем уравнение пьезопроводности в цилиндрической системе координат

. (4.12)

, (4.13)

Найдём значения постоянных. Для этого будем считать, что в момент времени t = t/ давление в пласте было р = рк = const. Тогда при r > 0 и при t = t/ второй член правой части обращается в неопределённость типа ¥/¥ и определяется по правилу Лопиталя, что даёт С = рк. Таким образом,

. (4.14)

dtз = b*Dрdt0 = . (4.15)

. (4.16)

Таким образом в случае скважины, введенной в неограниченный пласт в некоторый (начальный) момент времени и действующей мгновенно, изменение давления во времени определяется соотношением:

. (4.17)

Если скважина была введена в некоторый момент времени и действовала непрерывно с постоянным дебитом Q = Q0 в течение времени dt/, то за этот промежуток времени через сток выделяется из пласта объём

dt2 = Qdt/ и, следовательно, из (4.17) следует

. (4.18)

Интеграл правой части носит название интегрально-показательной функции

и с учетом данного обозначения решение для изменения давления запишется в виде

. (4.19)

Формула (4.19) является основной формулой теории упругого режима пласта.

Интегрально-показательная функция имеет вид (рис.4.1) и обладает следующими свойствами:

(4.20)

Для малых значений u

, (4.21)

с погрешностью, не превышающей 0,25% при u

. (4.22)

С учетом соотношения (4.21) основное уравнение (4.19) перепишется в виде, которое более известно под названием уравнение кривой восстановления давления (КВД)

. (4.23)

Рис. 4.2. Пьезометрические кривые при пуске скважины в бесконечном пласте с постоянным дебитом

Полученную зависимость можно использовать при числе Фурье с погрешностью, не превышающей 0,6%. Практически это означает, что уже через 1 с после пуска скважины расчеты забойного давления, выполненные по формуле (4.23), будут иметь погрешность не превышающую 0,6%. Формулу (4.23) можно использовать и для расчета падения давления в конечном пласте, а именно, погрешность расчета давления при этом не превышает 1%, если rк > 1000rc и fo

Рассмотрим пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса rc c постоянным дебитом Q0 (рис.4.2). Для точек вблизи забоя можно пользоваться формулой (4.23), а дифференцируя её по координате r, найдём градиент давления

.

Из этой формулы следует, что градиент давления для значений r, удовлетворяющих неравенству r2

4.1.4.2. Анализ основной формулы теории упругого режима

Основная формула (4.19) или (4.23) строго говоря справедлива лишь для точечного стока, т.е. при rс=0. Практические расчеты показывают, что ей можно пользоваться даже для укрупнённых скважин (rс

1км) и нельзя использовать только в первые доли секунды после пуска скважины. Если скважина укрупнённая, то формула (4.23) может дать большую погрешность лишь вблизи от её стенки (контура). Чем дальше отстоит от этого контура точка, в которой определяется давление, и чем больше времени прошло с момента пуска укрупнённой скважины, тем меньше погрешность.

Анализ формулы (4.23) показывает, что вскоре после пуска скважины вокруг неё начинает непрерывно увеличиваться область пласта (рис.4.2), в которой для каждого момента времени давление распределяется так, как и при установившемся движении, т.е. давление оказывается квазиустановившимся и пьезометрические кривые будут кривыми логарифмического типа.

Из (4.23) следует, что градиент давления, расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются соотношениями:

(4.24)

Из данных соотношений следует, что стационарная скорость достигается очень быстро на небольших расстояниях от скважины, так как значение коэффициента пьезопроводности велико.

4.1.4.3. Приток к скважине в пласте конечных размеров в условиях упруго-водонапорного и замкнуто- упругого режима

Круглый горизонтальный пласт с открытой внешней границей

с открытой внешней границей:

Постоянный дебит. Пусть пласт имеет внешнюю границу радиусом rк, через которую может поступать вода при истощении упругого запаса. В центре пласта имеется скважина радиусом rс, которая мгновенно запускается в эксплуатацию с постоянным дебитом Q0. Перед пуском скважины давление в пласте было рк.

Для определения давления используем полученную ранее зависимость

, (4.19)

для неограниченного пласта и формулу Дюпюи

(4.25)

для установившегося плоскорадиального потока. В результате совместного решения данных зависимостей получим следующую приближённую формулу

, (4.26)

Рис. 4.4. Изменение дебита скважины с течением времени при постоянном забойном давлении рс

Изменение пьезометрической кривой в различные моменты времени после пуска скважины с постоянным дебитом в пласте с круговым контуром питания показано на рис.4.3а.

Круглый горизонтальный пласт с закрытой внешней границей

Рис. 4.4. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при

Постоянный дебит. Будем считать дебит скважины постоянным. Пьезометрические кривые падения давления для разных моментов времени показаны на рис. 4.4. С некоторого момента смещение во времени пьезометрической кривой для закрытого пласта происходит так, что все точки её опускаются на одно и тоже расстояние d, т.е. во всех точках пласта давление падает с одной скоростью.

Из рассмотрения рис. 4.3, 4.4. видно, что в условиях упругого режима процесс перераспределения давления, а значит, и процесс взаимодействия скважин развивается постепенно, если же и наблюдается аномально быстрое взаимодействие скважин, то это можно объяснить неоднородностью пластов и их анизотропией.

Кроме того, при пуске или остановке скважины давление вначале меняется быстро, а затем темп изменения давления замедляется.

Если скважина действовала с постоянным дебитом при установившимся потоке и в некоторый момент времени она останавливается, то начинается процесс восстановления давления. Уровень жидкости в скважине начинает подыматься.

Для расчета используются полученные выше формулы для возмущающей скважины, но вместо данных понижения давления в пласте надо подставить данные повышения давления после остановки скважины.

Рис. 4.6. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном забойном давлении

Рис. 4.7. Изменение дебита Q (кр.1) скважины и суммар-ной добычи Qcp (кр.2) с течением времени t

Постоянное забойное давление. Объемный дебит возмущающей скважины определяется по формуле

(4.27)

а объем жидкости tж, добытой из скважины (в пластовых условиях) за время t с момента пуска скважины равен

.

При больших параметрах Фурье fo объем Qж оказывается равным упругому запасу жидкости в закрытом пласте

4.1.4.4. Определение коллекторских свойств пласта по данным исследования скважин нестационарными методами

Наиболее распространен метод определения коллекторских свойств по данным о восстановлении забойного давления (КВД) в остановленных скважинах в полулогарифмических координатах (Dр, lnt) на основе зависимости (4.30), записанной относительно забоя скважины в виде

(4.34)

Уравнение (4.34) можно рассматривать как уравнение изменения забойного давления после остановки скважины, работающей до этого с постоянным дебитом Q.

По известным коэффициентам можно определить коллекторские свойства пласта:

· по коэффициенту i определяют гидропроводность пласта

. (4.35)

· Если известна вязкость жидкости в пластовых условиях m и толщина пласта h, то из последней формулы находится коэффициент проницаемости пласта:

. (4.36)

· По известному угловому коэффициенту i = tgj и радиусу rc скважины из коэффициента А можно определить коэффициент пьезопроводности пласта.

В случае ограниченого пласта, когда изменение давления, вызванное закрытием скважины, доходит до его границы, КВД начинает искажаться, а через достаточно большое время выходит на горизонтальную асимптоту, соответствующую стационарному распределению давления. Поэтому длина прямолинейного участка на кривой КВД ограничена.

Кроме того, в реальных условиях скважину нельзя остановить мгновенно. После её закрытия на устье приток флюида из пласта продолжается ещё некоторое время из-за упругости жидкостей и газов, заполняющих скважину. Время выхода на асимптоту должно, очевидно, превышать время дополнительного притока. Поэтому возможны условия, при которых прямолинейный участок на КВД появляется через значительный промежуток времени, либо даже вообще отсутствует.

На форму КВД сказывается также несовершенство скважины и возможное нарушение закона Дарси у стенок скважины. В этом случае необходимо решение более сложного уравнения пьезопроводности с нелинейными членами и использование приближенных методов расчета коллекторских свойств.

Источник