Расшифруй числовой ребус если известно что
Скоро вебинар
«ПРЯМАЯ НА ПЛОСКОСТИ»
(Аналитическая геометрия). Жми подробнее.
В «буквенном» ребусе каждая буква означает одну определенную цифру. Одинаковым буквам соответствуют одинаковые цифры. По-другому эти ребусы называют еще криптоарифметическими задачами или криптарифмами.
В ребусах со звездочками, квадратиками и т. д. каждый значок может обозначать любую из десяти цифр — от 0 до 9. Одни цифры могут повторяться несколько раз, а другие вообще оставаться неиспользованными.
В ребусах с буквами и значками (звездочками, квадратиками, кружочками, точками и т. п.) вместо значков могут стоять любые цифры, в том числе и зашифрованные буквами.
Помните: ни одно число не начинается нулем.
Расшифровать ребус — это значит восстановить первоначальную запись примера.
При решении задач такого типа требуется внимательность к очевидным арифметическим действиям и умение вести нить логических рассуждений. Рассмотрим решение некоторых арифметических ребусов.
ПРИМЕР
Число палиндром
Умножив два числа, получаем число, обратное первому множителю. Что это за числа?
3. Так как при умножении четырехзначного числа (первая цифра, которого равна 1) на 9, получаем четырехзначное число первая цифра, которого равна 9, следовательно, вторая цифра (первого множителя) может быть только 0 или 1 при умножении на 9 (иначе число-результат будет пятизначным числом ). Но 1 мы уже использовали, поэтому буква О – это цифра 0. Т.е. получаем
4. Осталось найти букву Р. Начнем умножать столбиком: 9*9=81.
1 пишем в разряд единиц, 8 переносим в следующий разряд
т. е. при умножении Р на 9 число единиц равно 2. Следовательно Р=8. Таким образом, получаем: 1089*9=9801.
ПРИМЕР
Каникулярный
1. Сумма двух целых положительных однозначных чисел не может превосходить 18, поэтому при поразрядном сложении двух чисел в высший разряд может быть перенесена лишь 1. Отсюда П=1, а Л, Е, Т, О не равны 1.
3. 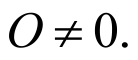
4. О+О=Т, следовательно Т- четное.
5. Л не равно 5. Так как если бы Л=5, то
6. Л не равно 6. Так как если бы Л=6, то
7. Л не равно 7. Так как если бы Л=7, то
9. Л не равно 9. Так как если бы Л=9, то
Получаем: 8947+8947=17894
ПРИМЕР
Умножение
ПРИМЕР
Пятью пять
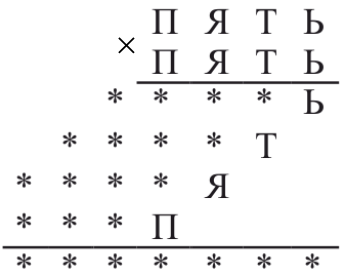
Букве Ь можно поставить в соответствие цифры 0,1,5,6 ( так как 0*0=0, 1*1=1, 5*5=25, 6*6=36). 0 и 1 не годятся, так как третья строка 5-значное число. Если Ь это 5, то строки с третьей по шестую будут оканчиваться на 0 или 5 (при умножении на 5 – число заканчивается на 0 или 5). У нас все строки оканчиваются различными цифрами, следовательно, Ь=6.
Среди цифр, соответствующих буквам П,Я,Т, нет нуля, так как четвертая и пятая строки – 5-значные числа и множители не могут начинаться с цифры 0 (случай для шестой строки).
Статья «Решение числовых ребусов»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Миллионы людей во всех частях света любят разгадывать ребусы. И это не удивительно. “Гимнастика ума” полезна в любом возрасте. Ведь ребусы тренируют память, обостряют сообразительность, вырабатывают настойчивость, способность логически мыслить, анализировать и сопоставлять.
Вся наша жизнь – беспрерывная цепь игровых ситуаций. Они бывают, значительны, а бывают, пустячны, но и те, и другие требуют от нас принятия решений. Еще в Древней Элладе без игр не мыслилось гармоническое развитие личности. И игры древних не были только спортивными. Наши предки знали шахматы и шашки, не чужды им были ребусы и загадки. Таких игр во все времена не чуждались ученые, мыслители, педагоги. Они и создавали их. С древних времен известны головоломки Пифагора и Архимеда, русского флотоводца С.О. Макарова и американца С. Лойда.
Существует такая разновидность ребусов, которые называются числовыми. Они представляют из себя выражения, требующие арифметического решения, составленные в виде математических равенств, где числа заменяются другими знаками – буквами, фигурками геометрии, звездочками и т.д.
Под числовыми ребусами подразумевают те задачки, в которых необходимо использовать логические рассуждения. Именно они являются способом решения и расшифровывания каждого символа, который ведет к восстановлению числовой записи.
Числовым ребусам уже почти тысяча лет. Впервые они появились в Китае, затем в Индии. В европейских странах числовые ребусы поначалу называли крипт-арифметические задачи. Их появление в Европе впервые было отмечено только в двадцатом веке, несмотря на то, что развитие математики началось много столетий назад.
При составлении ребусов числового типа пользуются следующими правилами. Все использующиеся цифры заменяют буквами. При наличии в задаче одинаковых цифр, соответственно, используется такое же количество букв. Промежуточные стадии математических операций обозначаются звездочками. Различают на основе этих правил несколько типов ребусов. Первый – это ребусы, в которых заменены на цифры все имеющиеся буквы. При этом зашифровывается какое-либо выражение, которое обозначает житейские ситуации в оригинальном изложении.
Числовые ребусы являются очень сложными, порой попадаются такие, которые требуют поэтапного длительного решения. Числовые ребусы являются увлекательными математическими задачами, которые сильно развивают логику и сообразительность.
Числовые ребусы могут быть составлены из нескольких рядов символов, а между ними ставится определенное количество математических знаков, которые являются указателями для того, какие действия необходимо произвести по вертикали, а какие по горизонтали.
1) ТА+ ИТ = ЛЕТ 2) КРА + ОЛИ = ИАЯ
ЕС х СН = ЛЛАС Л х АР= КЯИ
ЛЕАА + ЕЦ = ЛЕЕЦ ОИИ + АЛ = РКА
Числовые ребусы являются очень популярными не только в школах на обычных уроках, но и на математических олимпиадах. решить числовые ребусы можно с помощью компьютерных программ, однако ни с чем несравнимое удовольствие может получить человек, который самостоятельно ломает голову над разгадкой и в конце концов ее находит.
Задачи, представленные в занимательной форме, очень интересны. Их хочется решать, они увлекают своей необычностью, неочевидностью ответа. Появляется желание совершить пусть даже нелёгкий путь поиска решения. Занимательность и строгость вполне совместимы. Каждое самостоятельно решенное задание – это возможно, небольшая, но всё же победа.
В буквенных ребусах каждой буквой зашифрована одна определенная цифра: одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы.
В ребусах зашифрованных, например, звездочками, каждый символ может обозначать любую цифру от 0 до 9. Причём, некоторые цифры могут повторяться несколько раз, а другие не использоваться вовсе.
Перед началом решения математического буквенного ребуса (например, криптарифма), убедитесь, что в нём использовано не более 10 различных букв. В противном случае, такой ребус не будет иметь решений.
Начните решение ребуса с правила, согласно которому ноль не может быть крайней левой цифрой в числе. Таким образом, все буквы и знаки, с которых начинается число в ребусе, уже не могут обозначать ноль. Круг поиска нужных цифр сузится.
В ходе решения отталкивайтесь от основных математических правил. Например, умножение на ноль всегда дает ноль, а при умножении любого числа на единицу, мы получим в результате исходное число.
Очень часто математические ребусы представляют собой примеры сложения двух чисел. Если при сложении сумма имеет больше знаков нежели слагаемые, значит сумма начинается с «1»
Обращайте внимание на последовательность арифметических действий. Если числовой ребус состоит из нескольких рядов знаков, он может решаться как по вертикали, так и по горизонтали.
Не бойтесь совершать ошибки. Возможно, они подскажут вам верный ход решения. Не пренебрегайте методом перебора. Некоторые ребусы потребуют длительного поэтапного решения, но в итоге вы будете вознаграждены верным ответом и отличной разминкой для вашей сообразительности.
Прежде чем приступить к разгадыванию сложных задач, потренируйтесь на простом примере: ВАГОН+ВАГОН=СОСТАВ. Запишите его в столбик, так будет удобнее решать. Вы имеете два неизвестных пятизначных числа, сумма которых шестизначное число, значит В+В больше 10-ти и С равно 1. Замените символы С на 1.
Сумма А+А – однозначное или двухзначное число с единицей на конце, это возможно в том случае, если сумма Г+Г больше 10 и А равно либо 0, либо 5. Попробуйте предположить, что А равно 0, тогда О равно 5-ти, что не удовлетворяет условиям задачи, т.к. в этом случае В+В=2В не может равняться 15-ти. Следовательно, А=5. Замените все символы А на 5.
Сумма О+О=2О – четное число, может быть равна 5 или 15 лишь в том случае, если сумма Н+Н – двухзначное число, т.е. Н больше 6-ти. Если О+О=5, то О=2. Это решение неверно, т.к. В+В=2В+1, т.е. О должно быть число нечетное. Значит, О равно 7-ми. Замените все О на 7.
Легко заметить, что В равно 8-ми, тогда Н=9. Замените все буквы на найденные числовые значения.
Замените в примере оставшиеся буквы на числа: Г=6 и Т=3. Вы получили верное равенство: 85679+85679=171358. Ребус отгадан.
Как решать математические ребусы
В разряде единиц отметим сразу отсутствие переноса («0»). |
М=1, поскольку сумма двух слагаемых всегда начинается с 1 если знаков суммы (5) больше чем знаков слагаемых (по 4). Также отмечаем перенос 1 из разряда тысяч (S+M=O) в разряд десятков тысяч (M). |
В разряде тысяч S+1(М)=O, причём эта сумма больше 9 т.к. даёт перенос (1 «в уме») в разряд десятков тысяч благодаря которому М=1. В данном случае единственным возможным значением для О=0, поскольку перенос 1 из разряда тысяч в разряд десятков тысяч возможет при S=9 либо S=8 и перенос 1 с разряда сотен. (При S=9 и переносе 1 из разряда сотен О=1, что не допустимо т.к. «1» уже занята «М»). |
Мы выяснили, что S=9 либо S=8 и перенос 1 с разряда сотен (E+O=N > 9). Предположим, что S=8, в таком случае в разряде тысяч получаем: 1(перенос из разряда сотен) + 8(S) + 1(M) = 0(O) + перенос 1 в разряд десятков тысяч. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поскольку S не может равняться 8, получаем S=9. Переноса из разряда сотен (E+O=N) нет, поскольку в таком случае в разряде тысяч получим: 1(перенос из разряда сотен)+9(S)+1(М)=1+1 перенос в рязряд десятков тысяч. Т.е. получичли О=1, что не верно т.к. ранее мы выяснили, что М=1. |
Рассмотрим разряд сотен: E+0(О)=N. Очевидно, что это возможно, если «1» переносится из разряда десятков. Причём сама сумма E+0=N меньше 10 т.к. ранее мы выяснили, что переноса в разряд тысяч нет. |
В разряде сотен получаем: 1(перенос из разряда десятков)+Е+0(О)=N. Поскольку ранее мы выяснили, что N 2 (т.к. Е>1). Предположим, что N=3 и соответственно Е=2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если мы посмотрим на разряд единиц (D+E=Y), то очевидно, что он не даёт переноса в разряд десятков, т.к. максимально возможное значение D=6 (7+2=9-занята, 8+2-10-ноль занят, 9 занята). В разряде десятков получаем R=9, что не верно, т.к. «9» занята |
Вернёмся назад и теперь предположим, что N=4 и соответственно Е=3 |
Если мы посмотрим на разряд десятков (N+R=E), то единственное возможное значения для R=8 и перенос из разряда единиц |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вернёмся назад и теперь предположим, что N=5 и соответственно Е=4 |
Если мы посмотрим на разряд десятков (N+R=E), то единственное возможное значения для R=8 и перенос из разряда единиц |
|
Вернёмся назад и теперь предположим, что N=6 и соответственно Е=5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если мы посмотрим на разряд десятков (N+R=E), то единственное возможное значения для R=8 и наличие переноса из разряда единиц |
В разряде единиц получаем: D=7, Y=2 Решение найдено: 9567+1085=10652. Данный математический ребус имеет единственное решение. Впрочем, имеется возможность повторить всё самостоятельно, без подсказок ► Наверх
|

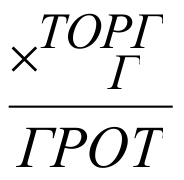
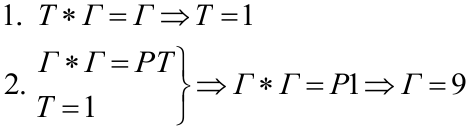
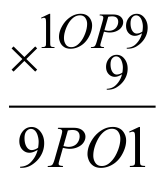
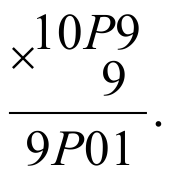


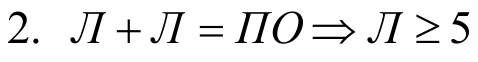












 Полезный совет:
Полезный совет: