Равенство и уравнение в чем разница
Что такое числовые выражения, равенства, неравенства и уравнения
Выражение
Числовое выражение — это числа, соединённые знаками арифметических действий: сложение, вычитание, умножение и деление.
Найти значение числового выражения — это значит выполнить все указанные арифметические действия и получить конкретное число.
Кроме арифметических действий выражения могут содержать скобки, которые влияют на порядок действий при решении выражения.
Пример 1:
Равенство
Равенства — это числа или выражения, соединённые знаком = (равно).
Равенство считается верным, если числа или числовые выражения слева и справа от знака =, имеют равное значение.
Равенство считается неверным, если числа или числовые выражения слева и справа от знака =, не равны (≠).
При решении равенств соблюдается следующий порядок действий:
Пример 2:
1) 5 = 7 — равенство неверно, так как 5 ≠ 7.
2) 36 : 2 = 6 • 3 — равенство верно, так как:
3) 48 + 9 = 54 — 1 — равенство неверно, так как:
Неравенство
Пример 3:
1) 5 > 7 — неравенство неверно, так как 5
3) 4 + 5 • 6 > (4 + 5) • 6 — неравенство неверно, так как:
Уравнение
Уравнение — это равенство, которое содержит неизвестное число, обозначенное какой-либо латинской буквой: x, y, a, b, z, d и т.д.
Корень уравнения — это число, при подставлении котрого вместо буквы в равенство делает это равенство верным.
Решить уравнение — это значит найти все возможные корни уравнения.
Порядок и правила решения уравнений зависят от того, к какому типу они относятся:
Тождество — что это такое в математике
Очень часто в математике встречаются такие слова «тождество», «тождественно равные», «тождественное преобразование». Многие учащиеся путают значения этих слов. Давайте с вами разберемся, что означают эти слова.
В математике и, в более общем плане, в научных областях тождество — это открытие, что два математических объекта (имеющих два разных математических сценария) на самом деле являются одним и тем же объектом. В частности, тождество — это равенство между двумя выражениями, которое истинно независимо от значений различных используемых переменных. Тождества обычно используются для преобразования одного математического выражения в другое, особенно для решения уравнения.
Определение тождества
Равенство, которое является верным при любом значении, входящей в него переменной, называется тождеством. Тождество, как и уравнение, имеет переменную — x, y или любую другую букву. Разница между тождеством и уравнением заключается в том, что уравнение имеет корень — то есть значение переменной, при которой выполняется данное равенство. А в тождестве равенство должно выполняться при любом значении переменной. То есть, равенство не всегда будет тождеством.
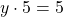
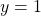
А равенство 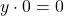
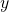
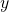
Пример: 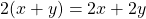
Уравнение или тождество
Как и уравнение, тождество имеет переменную. Уравнение содержит вопрос: при каких значениях переменной получается равенство. Тождество — это утверждение в том, что равенство верно при любом значении переменной.
Определите, где в перечисленных ниже выражениях будет тождество, а где только уравнение.
Вы увидите, что все выражения, кроме третьего, являются уравнениями. А тождество у нас получается только в третьем выражении, так как при раскрытии скобок в правой части уравнения, мы получаем взаимоуничтожение переменных в правой и левой частях равенства, которое остается верным.
Очень часто тождества используются в тригонометрии. Вы можете посмотреть статью на эту тему подробнее: тригонометрические тождества часть 1 и тригонометрические тождества часть 2.
Например, самое известное, так называемое основное тригонометрическое тождество:
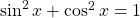
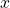
Некоторые алгебраические тождества квалифицируются как «замечательные» и позволяют облегчить вычисление или факторизацию полиномиальных выражений.
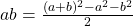
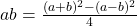
То есть, умножение осуществлялось с помощью вычитания квадратов чисел — для этого у вавилонян имелись таблицы квадратов чисел.
А еще вы можете ознакомиться с основным логарифмическим тождеством. Удачи при изучении математики.
Равенство, тождество, уравнение.
Знак равенства используется в математике очень часто, и смысл, который придается этому знаку, далеко не всегда один и тот же. Так, часто мы соединяем знаком равенства два числа, например:
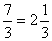
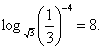
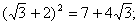
Каждая такая запись представляет собой некоторое высказывание, которое может быть истинным или ложным. Среди приведенных выше четырех высказываний такого рода второе, третье и четвертое являются истинными, а первое — ложным.
Для того чтобы убедиться в истинности (или ложности) такого высказывания, нередко бывает нужно произвести те или иные действия: сложение дробей, разложение на множители, возведение суммы двух чисел в квадрат и т. п. Однако смысл знака равенства во всех этих случаях один и тот же: истинность такого высказывания означает, что слева и справа от знака равенства стоит одно и то-же число (только, может быть, записанное по-разному).
Высказывания такого вида мы будем называть числовыми равенствами. Если некоторое числовое равенство представляет собой истинное высказывание, то для краткости говорят: «это — верное равенство». Так, равенство (2) — верное. Если же некоторое числовое равенство представляет собой ложное высказывание, то для краткости говорят: «это—неверное равенство». Так, (1) —неверное равенство.
В ином смысле применяется знак =, когда идет речь о равенстве функций. Напомним, что две функции f (х) и g (х) считаются равными (т. е. совпадающими), если, во-первых, области определения этих двух функций совпадают и, во-вторых, для любого числа х0, принадлежащего общей области определения этих функций, значения функций в точке х0 совпадают, т. е. верно числовое равенство f (х0) = g(x0). Равенство функций (х) и g(x) обычно выражают записью f(x) = g(x).
Например, мы пишем (х 2 + 1) 6 = х 3 + Зx 4 +. Зx 2 + 1, выражая этой записью тот факт, что слева и справа от знака = стоят равные функции (т. е. слева и справа стоит одна и та же функция, только, может быть, записанная по-разному).
В записи, выражающей равенство (т. е. совпадение) двух функций, вместо знака = часто используют знак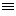
Запись f(x)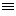
Подчеркнем еще раз: когда мы говорим, что f(x) = g(x) есть тождество, то это означает, что области определения функций f(х) и g(х) совпадают и при этом для любого х0, принадлежащего этой области определения, справедливо числовое равенство f(x0) = g(x0).
Примерами тождеств могут служить соотношения:
(x + 1) 2 = x 2 + 2x + 1,
Иногда при рассмотрении тождеств приходится ограничивать области определения функций. Именно, будем говорить, что равенство f(x) = g(x) является тождеством на множестве М, если, во-первых, множество М содержится в области определения каждой из функций f(x), g (х) и, во-вторых, для любого числа х0, принадлежащего множеству М, справедливо числовое равенство f(x0) = g (x0) В этом случае пишут:
. Пример 1. Равенство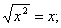
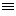

Заметим, что обе функции y=
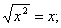
Пример 2. Рассмотрим равенство arcsin(sinx) =





(а — 1)(а 2 + а + 1) = а 3 — 1
являются тождествами на множестве всех действительных чисел (или даже на множестве всех комплексных чисел), Можно также рассматривать функции, зависящие от двух или большего числа аргументов, и писать тождества для таких функций. Конечно, и в этом случае надо указывать, при каких значениях аргументов написанное равенство является тождеством.
Например, равенство log2 a b = b log2 a является тождеством при а > 0 и любом действительном b; равенство
является тождеством при x





где f(х) и g(x) — произвольные функции, Таким образом, по внешнему виду уравнение выглядит так же, как и тождество: две функции, соединенные знаком равенства. Но когда мы говорим, что соотношение (5) есть уравнение, то это показывает наше отношение к этому равенству. Именно, когда мы говорим, что (5) есть уравнение, то это означает, что равенство (5) рассматривается как неопределенное высказывание (при одних значениях х истинное, при других—ложное), и мы интересуемся нахождением корней этого уравнения, т. е. таких значений х, при подстановке которых это неопределенное высказывание становится истинным. Более подробно, корнем (или решением) уравнения называется всякое число, при подстановке которого вместо неизвестного в обе части уравнения получается справедливое (верное) числовое равенство. Но что значит «получается справедливое числовое равенство»? Это означает, во-первых, что при подстановке этого числа вместо неизвестного все действия, обозначенные в левой и правой частях уравнения, оказываются выполнимыми и, во-вторых, в результате выполнения этих действий в левой и правой частях получается одно и то же число. Иначе говоря, число а называется корнем уравнения (5), если, во-первых, это число принадлежит как области определения функции f(x), так и области определения функции g(x) и, во-вторых, значения этих функций в точке а совпадают, т. е. Итак, если сказано, что равенство (5) рассматривается как уравнение, то это означает, что мы интересуемся нахождением корней этого уравнения, т. е. тех значений, которые обращают соотношение (5) в верное числовое равенство. Пример 4. Если рассматривать уравнение |х| = х на множестве всех действительных чисел, то всякое неотрицательное число является корнем этого уравнения (других корней нет). Пример 6. Уравнение cosx = 2 не имеет решений на множестве действительных чисел, так как |cosx0| Если найдена некоторая совокупность значений х, каждое из которых является корнем уравнения f (x)=g(x), то это еще не значит, что мы решили уравнение. Решить уравнение — значит найти все его решения (или доказать, что уравнение не имеет решений). Пример 8. Равенство Пример 9. Бессмысленно ставить вопрос, является ли соотношение 0·x + 5 = 5 тождеством или уравнением. Мы можем сказать, что оно является тождеством на множестве всех действительных чисел. Но мы можем также рассматривать это соотношение как уравнение и тогда скажем, что корнями этого уравнения являются все действительные числа. Замечание. Кроме рассмотренных выше случаев использования знака = в математике встречаются и другие. Так, выражение вида «рассмотрим функцию f(x) = x 3 — Зх 2 + 5x + 11» часто используется в качестве определения. В этом случае знак = имеет тот смысл, что всюду в проводимом рассуждении f (х) будет обозначать именно эту функцию. Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия, Поясните пожалуйста различие терминов «тождество» и «равенство». В википедии написано как-то непонятно, с одной стороны, тождество это то что выполняется всегда, а равенство не всегда, а с другой, там сразу же написано что и тождество может выполняться не всегда. Например Еще я так понял, что равенство (например в алгебре), это какое угодно выражение, которое содержит знак «равно», то есть например выражение Последний раз редактировалось warlock66613 15.09.2016, 13:06, всего редактировалось 8 раз(а). Понятием «тождество» в интересующем вас смысле оперируют чаще в приложениях (в той же физике), а не собственно в математике. И, в принципе, это нестрогий термин (в метаматематике есть строгое понятие «тождество», но это несколько иное). Когда про некоторое алгебраическое равенство говорят, что «это тождество», то хотят подчеркнуть, что оно справедливо при любых значениях входящих в него переменных. Что подразумевается под «любыми» значениями надо выяснять из контекста, но это обычно очевидно. Математики же ожидаемо предпочитают оперировать не понятием «тождество», противопоставленным просто «равенству», а одним понятием «равенство», но применяя его к разным объектам. Так, вместо того, чтобы сказать, что А слово «тождественность» вообще по сути синоним слова «равенство». Так, в примере выше можно было сказать, что функции тождественны, что означало бы ровно то же самое. Последний раз редактировалось Munin 15.09.2016, 16:57, всего редактировалось 3 раз(а). Последний раз редактировалось Sonic86 15.09.2016, 14:28, всего редактировалось 7 раз(а). Последний раз редактировалось wrest 15.09.2016, 15:52, всего редактировалось 2 раз(а). Я только вижу, что «тождество» более сильное выражение чем «равенство», но и то и другое может быть справедливо (выполняться) или нет в зависимости от каких-то условий, поэтому если я читаю «a равно b» и «а тождественно равно b», я не вижу разницы и думаю что «а и b равны друг другу всегда». Замечание тов. Munin насчет уравнения понятно, об уравнении говорят когда заранее неизвестно для каких значений переменных оно выполняется (есть ли корни), и именно нахождение всех или некоторых этих условий (или определение что таких условий не существует) представляет цель записи уравнения. Если перейти к физике, то запись например закона Ньютона Пара примеров употребления. Зачем тут слово «тождественно»? Правильно ли я понимаю, что речь в этом коротком предложении, если не читать что написано до и после него, идет о том, что для каждого элемента матрицы Там же, через пару страниц, Фихтенгольц пишет То есть, дифференцируя уравнения, мы получаем уже не уравнения, а равенства! У вас тут есть некоторая путаница, которую я хотел бы по возможности исправить. Это довольно частая ситуация в математике, когда какую-то вещь начинают рассматривать не как задачу, а как объект, и исследовать уже по-разному. При этом, «ответы на задачу» могут быть известными и включёнными в неё. Или нет. Тогда отдельно можно искать «ответы», а отдельно можно исследовать объект, не занимаясь таким поиском. Знак Мне страшно вам отвечать на этот вопрос. Не 5 курс мехмата точно, остальное подойдет 🙂 Фихтенгольц, к слову, был моим любимым учебником по матану. «Официальным» был, кажется, Кудрявцев, но в студенческой среде бытовало твердое убеждение что Фихтенгольц лучше, ну и мне так казалось тоже. Например, в Фихтенгольце Последний раз редактировалось arseniiv 15.09.2016, 18:27, всего редактировалось 1 раз. Хотя или не называется, т. к. попадалась такая конструкция, кажется, только в равенствах какой-то другой функции. Последний раз редактировалось user14284 15.09.2016, 18:43, всего редактировалось 3 раз(а). Предлагаю ТС не усложнять себе жизнь, а считать их синонимами. Вы ничего не потеряете. Сейчас этот форум просматривают: нет зарегистрированных пользователей
f(a) = g
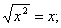
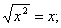
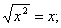
Научный форум dxdy
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные наукиПравила форума
Чем отличается тождество от равенства
В чем отличие между «а равно b» и «а тождественно равно b».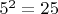
А 
Является ли 

Заслуженный участник 



Заслуженный участник Заслуженный участник Заслуженный участник Заслуженный участник 



Фихтенгольц в известном трехтомнике (просто это выловилось гуглем, а не то что вот именно Фихтенгольц или матрицы Якоби интересует) пишет


Заслуженный участник Заслуженный участник 
Заслуженный участник
Ближе всего 3 курс техвуза, но чувствую что вы ответите, что не надо было прогуливать и должен и так это знать. В техвузе преподавали классический анализ (дифференциальное и интегральное исчисление, включая функции комплексных переменных) если так можно выразиться, полностью, а функциональный анализ слегка.Заслуженный участник Заслуженный участник Кто сейчас на конференции