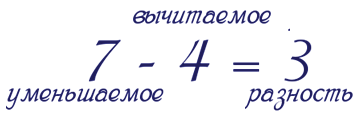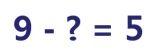Разность это что 1 класс
Вычитание
Познакомимся с вычитанием.
Рассмотрим числовой ряд и вспомним, в каком порядке идут числа.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
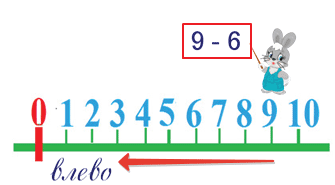
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Вычитает число 6.
Из какого числа он вычитает число 6?
Из числа 9. Мы поставили зайчика на число 9.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 6.
На каком делении он остановится? На числе 3.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
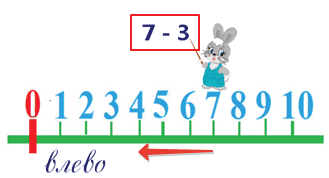
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Вычитает число 3.
Из какого числа он вычитает число 3?
Из числа 7. Мы поставили зайчика на число 7.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 3.
На каком делении он остановится? На числе 4.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
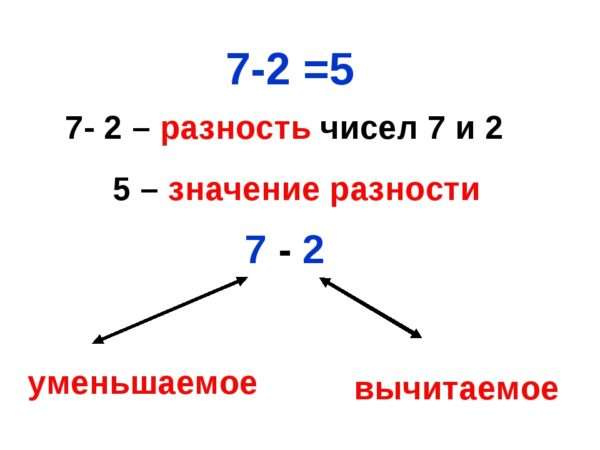
Как называются числа при вычитании?
Число, из которого вычитают, становится МЕНЬШЕ, уменьшается, поэтому его называют «уменьшаемое».
Число, которое вычитают, называют «вычитаемое».
Число, которое получается в результате вычитания, называют «разность».
У жонглёра было 9 шариков.
Когда несколько шариков упало, осталось ещё 5 шариков.
Сколько шариков упало?
Каким действием будем находить? Вычитанием.
Как называются числа при вычитании?
Как найти неизвестное вычитаемое
У жонглера было 9 шариков. Когда несколько шариков упало, осталось 5. Упали, значит, убрали.
Решаем вычитанием. Что нужно найти?
Нужно найти вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Как найти неизвестное уменьшаемое
Нужно найти уменьшаемое.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
5 + 4 = 9
Проверка вычитания
Если к разности прибавить вычитаемое, получится уменьшаемое.
Именно эта связь между разностью, уменьшаемым и вычитаемым используют для проверки вычитания.
Правильно ли произведено вычисление? Можно проверить так:
20 + 15 = 35, мы к разности прибавили вычитаемое и получили уменьшаемое. Значит, вычисление произведено верно и пример решен правильно.
Поделись с друзьями в социальных сетях:
Урок математики по теме «Уменьшаемое, вычитаемое, разность». 1-й класс
Класс: 1
Цели:
Ход урока
1. Мотивация к учебной деятельности
— Громко прозвенел звонок,
Он позвал вас на урок.
Мы будем примеры, задачи решать,
Выводы делать и рассуждать!
Ребята, сегодня у нас математики пройдет в нестандартной обстановке. На уроке вы должны быть внимательными, ответственными и активными. Покажите, как вы научились добывать знания и применять их.
2. Актуализация знаний и пробное учебное действие
1. «Потерялось число» (СЛАЙД 2)
— Что на слайде? (Числа)
— Как числа записаны? (По порядку при счете)
— Что заметили? (нет числа 7)
1 2 3 4 5 6 8 9 10
— Между какими числами стоит 7? (Между числами 6 и 8)
— За каким числом стоит число 7? (За числом 6)
— Перед каким числом стоит число 7? (Перед числом 8)
Оцените себя сигнальными карточками «+» и «-» Кто знал ответы на все вопросы поднимет карточку «+», а кто только на некоторые «-»
2. Самоопределение к деятельности. (СЛАЙД 3)
— Как рассказ называется? (задача)
— Сколько мотоциклов? (три) Маша, поставь на доску три треугольника.
— Сколько машинок? (четыре) Дима, поставь на доску четыре четырёхугольника.
— Какой вопрос будет у задачи? (сколько всего игрушек)
— Какое выражение выберем для решения задачи? (3+4=7)
— Прочитайте это выражение, используя знание компонентов действия сложения.
Оля: Первое слагаемое 4, второе слагаемое 3, значение суммы 7.
Миша: Сумма чисел 4 и 3 равна 7.
Оцените себя сигнальными карточками «+» и «-»
— Составьте задачу по рисунку: (СЛАЙД 4)
— Сколько всего шариков? (8) Рома, поставь на доску 8 кружочков.
— Что случилось? (шарик лопнул или улетел) Коля, убери один шарик.
— Какой вопрос будет у задачи? (сколько шариков осталось)
— Какое выражение выберем для решения задачи? (7-1=6)
— Как вы назовёте число 7? 1? 6?
Это выражение нельзя прочитать так, как первое.
3. Целеполагание и построение проекта выхода из затруднения
1. Целеполагание.
— Кто хочет узнать ответ на поставленный вопрос?
— Какая тема нашего урока?
Оля: Название компонентов действия вычитания.
— Это будет урок повторения или открытия новых знаний?
— А для чего нам нужны эти новые знания?
Саша: Чтобы грамотно говорить и хорошо считать.
— А в будущем, чтобы научиться решать уравнения и задачи. Значит, эти знания вам будут необходимы для дальнейшего обучения. Поэтому, какую цель поставим себе на уроке?
Влад: Запомнить названия чисел при вычитании.
Милена: Научиться по-новому читать выражения на вычитание.
— Верно, тема нашего урока название чисел при вычитании (СЛАЙД 5)
4. Выявление места и причины затруднения
— Почему не получилось? (Выявление причины затруднения.)
Миша: Мы не знаем, как называются числа при вычитании.
София: Мы не знаем компонентов действия вычитания.
— На какой вопрос нам предстоит ответить?
Саша: Мы должны узнать, как называются компоненты при вычитании.
1. Построение проекта выхода из проблемной ситуации.
(СЛАЙД 6)
— Перед вами пирожные. Сколько их? (7)
— Что произошло с количеством пирожных?
Катя: Оно уменьшилось.
— А что произошло с числом 7?
Саша: Оно тоже уменьшилось.
Работа в парах
— Как же мы будем называть это число при вычитании? У вас на партах лежат карточки с названием чисел (уменьшаемое, вычитаемое, разность, значение разности). Поработайте в паре друг с другом и выберите подходящий компонент для первого числа (проблемная ситуация).
— Не торопитесь, думайте, советуйтесь.
— Если выбрали, положите эту карточку перед ребёнком, сидящим на 1 варианте.
— Давайте вспомним, а что мы сделали с 1 пирожным?
Ярослав: Убрали.
Полина: Вычли.
София: Отняли.
— Подумайте, как можно назвать это число?
— Выберите, посовещавшись, карточку и положите её справа от первой.
— А теперь вы должны подумать и решить, как мы будем называть математическую запись со знаком «минус» и результат этого действия? Закончите выкладывать карточки по порядку.
— Работая в паре, вы сделали свои предположения. Как проверить их правильность?
Рита: Можно спросить у учителя или посмотреть в учебнике.
— Откройте учебник стр.29. Посмотрите в таблицу. Сравните со своей работой.
Проверка (СЛАЙД 7)
Оцените себя сигнальными карточками «+» и «-»
— Какое открытие мы с вами сделали?
Толя: Узнали компоненты действия вычитания.
— Попробуйте, опираясь на новые знания, прочитать выражение.
(СЛАЙД 8)
София: Уменьшаемое 7, вычитаемое 4, значение разности равно 6.
Захар: Разность чисел 7 и 1 равна 6.
Итак: В примере на вычитание, какое число из трёх самое большое? (Первое)
— Как вы думаете, почему?
(Дети выясняют, что это целое, из которого можно взять часть)
— Что происходит с первым самым большим числом при вычитании? (Оно уменьшается).
— Что происходит со вторым числом? (Его вычитают).
— А третье число (сообщает учитель) показывает разницу между первым числом и вторым.
— Вопрос “на сколько” задают при сравнении, чтобы найти разницу.
— Как же называется третье число? (Выясняется, что это РАЗНОСТЬ).
В ходе «открытия» нового знания на доске появляются названия чисел УМЕНЬШАЕМОЕ, ВЫЧИТАЕМОЕ, РАЗНОСТЬ, а также буквы –
У – В = Р
5. Физминутка
Для начала мы с тобой крутим только головой. (Вращение головой)
Корпусом вращаем тоже, это мы, конечно, сможем. (Повороты вправо и влево)
Напоследок потянулись, вверх и в стороны прогнулись. (Потягивания вверх и в стороны)
От разминки раскраснелись и за парты снова сели. (Сесть на место)
6. Первичное закрепление
— А сейчас нам предстоит научиться пользоваться новыми знаниями. Составьте задачу по иллюстрации. (СЛАЙД 9)
Оля: На ветке сидело 5 снегирей. 2 снегиря улетели. Сколько снегирей осталось?
— Когда снегири улетели, их осталось больше, чем было или меньше?
Паша: Их осталось меньше на 2.
— Что произошло с количеством снегирей на ветке?
Миша: Оно уменьшилось.
— Как узнать, сколько снегирей осталось?
Алина: Надо от 5 отнять 2 и получится 3.
— Прочитайте получившееся выражение.
Милена: Уменьшаемое 5, вычитаемое 2, значение разности равно 3.
Артём: Разность чисел 5 и 2 равна 3.
7. Включение в систему знаний и повторение. Самостоятельная работа
Учебник стр.29 № 1. (СЛАЙД 10)
Работа у доски: 9 – 4 = 5
Вероника: Уменьшаемое – это первое число, которое мы уменьшаем, поэтому мы записали 9. Вычитаемое – это число, которое мы вычитаем, значит, ставим знак минус и число 4. Мы вычислили результат – это 5. Значит значение разности равно 5.
Гимнастика для глаз.
Глазки вправо, глазки влево, и по кругу проведём.
Быстро – быстро поморгаем и немножечко потрём.
Посмотри на кончик носа и в «межбровье» посмотри.
Круг, квадрат и треугольник по три раза повтори.
Глазки закрываем, медленно вдыхаем.
А на выдохе опять глазки заставляй моргать.
А сейчас расслабились и на места отправились.
— Ребята, а сейчас вы будете работать самостоятельно. Работайте вдумчиво, не отвлекайтесь. Откроем рабочую тетрадь на странице 16 задание № 1. Прочитайте, что нужно сделать. На это странице 3 задания и после выполнения примеров каждый выберает себе задание которое может выполнить: либо задачу, либо геометрический материал.
Взаимопроверка (СЛАЙД 11)
Оцените себя сигнальными карточками «+» и «-».
8. Итог урока. Рефлексия
— Вот и подошёл к концу ещё один урок. Благодаря слаженной работе, взаимовыручке и поддержке друг друга, мы смогла повторить изученный материал и открыть новые знания.
— Какую задачу ставили?
— Какие новые знания получили на уроке?
— Что вам особенно понравилось?
— Что не совсем получилось, какие вы испытали трудности?
— У вас три волшебные буквы сегодняшнего урока. Прикрепите свою букву к моим на доске те, которые вам больше подходят
Уменьшаемое У (Удача Успех Умник Уяснил)
Вычитаемое В (Всезнайка Вдохновлён Всё понял Вдумчиво работал)
Разность Р (Рад помощи Растерялся )
Математика. 1 класс
Конспект урока
Математика, 1 класс
Урок № 35. Уменьшаемое. Вычитаемое. Разность. Использование этих терминов при чтении записей
Перечень вопросов, рассматриваемых в теме:
Вычитание – действие обратное сложению.
Уменьшаемое – число, из которого вычитают.
Вычитаемое – число, которое вычитают.
Разность – результат вычитания.
Слагаемое – число, которое складывают.
Сумма – результат сложения.
Обязательная литература и дополнительная литература:
Теоретический материал для самостоятельного изучения
Давайте решим задачу. В гараже стояли 5 машин. 2 машины уехали. Сколько машин осталось в гараже?
Для решения задачи выберем действие вычитание. Так как машины уехали, их стало меньше.
Ответ: 3 машины в гараже.
Как называются числа при вычитании?
Первое число 8 – число, из которого вычитают. Это уменьшаемое.
Второе число 5 – число, которое вычитают. Это вычитаемое.
Третье число 3 – результат вычитания. Это разность.
Выражение 8 – 5 тоже называется разность.
Равенство 8 – 5 = 3 можно прочитать так. Уменьшаемое – 8, вычитаемое – 5. Разность – 3. Или, разность восьми и пяти равна трем.
Назовем числа при вычитании.
6 – уменьшаемое, 2 – вычитаемое, 4 – разность. Выражение 6 – 2 тоже разность.
Соединим предложение с математической записью.
Уменьшаемое – 9, вычитаемое – 6. 8 – 3
Вычитаемое – 3, уменьшаемое – 8. 7 – 2
Разность чисел 7 и 2. 9 – 6
В коробке было 10 карандашей. Взяли 4 карандаша. Сколько карандашей осталось в коробке.
Для решения задачи выберем действие вычитание. Запишем разность чисел.
Ответ: 6 карандашей.
Ответим на вопросы, поставленные в начале урока.
Числа при вычитании называются уменьшаемое, вычитаемое, разность.
Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.
Выражение на вычитание можно читать по-разному. Например, 8 – 1 = 7
Уменьшаемое – 8, вычитаемое – 1, разность – 7. Или, разность чисел 8 и 1 равна 7.
Выполним несколько тренировочных заданий.
а) Вычитаемое – 3. Уменьшаемое – 5.
б) Разность чисел 7 и 2.
в) Сумма чисел 5 и 4.
Как найти разность чисел в математике
Содержание:
Само слово «разность» мы часто употребляем в нашей повседневной речи, объясняя им различие чего либо. Например, говоря о различии разных мнений и взглядов можно сказать о «разности» в них. Часто этот термин употребляется в науках, им обозначают разные количественные показатели, скажем разность электрических потенциалов, атмосферного давления или количества сахара в крови человека. Но прежде всего «разность» – это математический термин и об этой его ипостаси мы поговорим в нашей статье.
Арифметические действия с числами
Все основные арифметические действия с числами делятся на четыре большие группы:
Результат каждого из этих действий в свою очередь имеет свое уникальное название:
Роль в математике
Исходя из выше написанного, несложно дать определение того, что такое разность чисел, причем это понятие можно обозначить сразу несколькими способами:
Все эти определение разности являются правильными.
Как найти разность величин
Разность – это результат вычитания одного числа из другого. Первое из этих чисел, с которого делается вычитание, называют уменьшаемым, а второе число называется вычитаемым, его как раз вычитают из первого числа. Итак, чтобы найти значение разности чисел нужно просто от уменьшаемого отнять вычитаемое.
Тут все предельно просто, но при этом у нас появилось еще два дополнительных термина, которые также надо знать:
Итого, для того, чтобы найти разность необходимо знать значение уменьшаемого и вычитаемого, они должны быть известны.
Порой необходимо решить задачу обратную, при известной разности найти уменьшаемое или вычитаемое число. Сделать это тоже просто:
Примеры нахождения
Пример 1. Найти разницу двух величин.
Дано: 20 — уменьшаемое, 15 — вычитаемое.
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.
Пример 2. Найти уменьшаемое.
Дано: 48 — разность, 32 — вычитаемое значение.
Решение: 32 + 48 = 80
Ответ: 80.
Пример 3. Найти вычитаемое значение.
Дано: 7 — разность, 17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: 10.
И немного более сложных примеров, ведь в математике зачастую высчитывают разность с использованием не только двух, но и гораздо большего количества компонентов, в которых могут быть к тому же не только лишь целые числа, но и дробные, рациональные, иррациональные числа.
Пример 4. Найти разницу трех значений.
Даны целые значения: 56, 12, 4.
56 — уменьшаемое значение, 12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2) 44 — 4 = 40.
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми);
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
2) 56 — 16 = 40.
Ответ: 40 — разница трех значений.
Пример 5. Найти разницу величин 7 и 18.
Дано: 7 — уменьшаемое значение, 18 — вычитаемое.
Вроде все просто, но ведь вычитаемое у нас больше уменьшаемого, как быть в таком случае? В таком случае действует следующее правило: если вычитаемое больше уменьшаемого, то разность окажется отрицательной или другими словами, она будет числом со знаком минус.
Решение: 7 — 18 = —11
Ответ: —11 — отрицательное число со знаком минус.
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
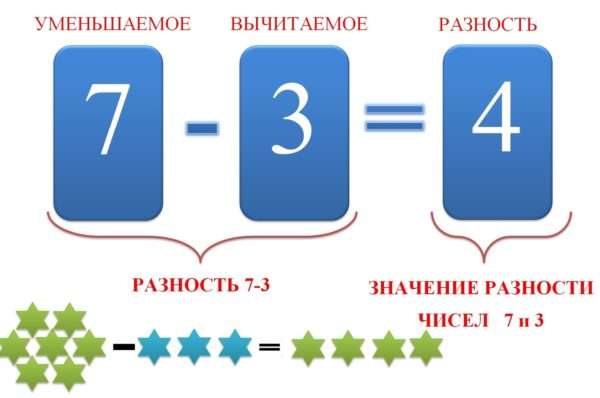
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.