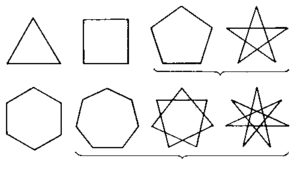
Какая фигура называется многоугольником что такое вершины стороны диагонали периметр

Математика. 5 класс

Конспект урока

Перечень рассматриваемых вопросов:

— наглядные представления о фигурах на плоскости;

— изображение геометрических фигур.

Многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Периметр многоугольника – это сумма всех его сторон.

Диагональ многоугольника – это отрезок, соединяющий две несмежные вершины многоугольника.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Мы уже знаем, из каких элементов состоят некоторые геометрические фигуры и как их изобразить на плоскости. Сегодня мы рассмотрим многоугольник.

Ломаная линия лежит в основе построения многоугольника.

Построим ломаную. Для этого отметим на плоскости несколько точек – например, пять. Соединим их так, чтобы никакие два из отрезков, имеющих общие точки, не лежали на одной прямой. Полученная фигура и будет ломаной, которую обозначают A, B, C, D, E.

Отрезки АВ, ВС, СD,DE называются звеньями ломаной. У ломаной, которую мы изобразили, четыре звена.

Если измерить длину каждого звена и найти их сумму, то получится длина ломаной.

Измерим длину ломаной.

Сумма длин всех звеньев равна:

АВ + ВС + СD + DЕ = 14 см – длина ломаной

Теперь нарисуем ломаную таким образом, чтобы её конец совпадал с началом. Получается замкнутая ломаная A, B, C, D, E, А.

Фигуру, образованную таким образом, называют многоугольником. То есть многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Стоит помнить, что многоугольником является как замкнутая линия, так и эта линия вместе с плоскостью внутри неё.

Такие звенья называются сторонами многоугольника. В нашем случае это стороны АВ, ВС, СD,DE, ЕА.

Углы, образованные двумя соседними сторонами, называют углами многоугольника, а их вершины – вершинами многоугольника.

∠А, ∠В, ∠С, ∠D, ∠E – углы многоугольника

Точки А, В, С, D, E – вершины многоугольника

Кроме того, у многоугольника есть ещё и диагонали.

Диагональ – это отрезок, соединяющий две несмежные вершины многоугольника. АС, СЕ – диагонали.

Сумма всех сторон многоугольника составляет периметр многоугольника.

P = АВ + ВС + СD + DЕ + ЕА

Рассмотрим разновидности многоугольников.

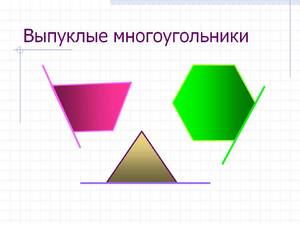
Многоугольник называется выпуклым, если он расположен по одну сторону от каждой прямой, содержащей его сторону.

Например, многоугольник ABCDE – выпуклый. А многоугольник MNKLO – нет.

По числу сторон многоугольники делятся на треугольники, пятиугольники и так далее.

Кроме того, многоугольники, у которых все стороны и все углы равны, называют правильными. Например, квадрат.

Многоугольники можно сравнить путём наложения. Если они полностью накладываются друг на друга, то считаются равными. При этом стоит помнить, они имеют одинаковые площади.

Для определения площади многоугольника надо выяснить, сколько раз выбранная единица измерения содержится в этой фигуре.

Не только человек может рисовать многоугольники. Природа тоже создаёт многоугольники в большом разнообразии. Рассмотрим, где они встречаются. Например, шестиугольники можно увидеть в сотах пчёл и – под микроскопом – в строении глаза мухи или некоторых других насекомых.

Панцирь черепахи тоже изобилует большим количеством многоугольников. Как и кожа змеи: она буквально покрыта многоугольниками. В общем, природа постаралась и разнообразила мир геометрическими фигурами.

№ 1. Чему равен периметр правильного шестиугольника со стороной 4 см?

Решение: для решения этой задачи достаточно вспомнить, что в правильных фигурах все стороны равны, следовательно, все стороны шестиугольника равны 4 см. Вычислим периметр шестиугольника, это сумма всех его сторон.

Р = 4 см + 4 см + 4 см + 4 см + 4 см + 4 см = 24 см

№ 2. Из листа железа размером 10 × 14 см вырезали два квадрата со стороной 4 см и три прямоугольника со сторонами 2см и 6см. Определите площадь остатка.

Решение: сначала найдём площадь листа:

S = 10 cм · 14 см = 140 см 2

Далее вычислим площадь квадратов со сторонами 4см:

S = 4 cм · 4 см = 16 см 2

Тогда площадь двух квадратов равна:

16 см 2 · 2 = 32 см 2

Найдём площадь прямоугольника:

S = 2 cм · 6 см = 12 см 2

Тогда площадь трёх прямоугольников равна:

12 см 2 · 3 = 36 см 2

Определим площади всех квадратов и прямоугольников, вырезанных из листа:

32 см 2 + 36 см 2 = 68 см 2

А теперь найдём площадь остатка: 140 см 2 – 68 см 2 = 72 см 2

Источник

Многоугольники

Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :

В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.

Выпуклые и вогнутые

Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:

Периметр

Сумма длин всех сторон многоугольника называется его периметром.

Периметр многоугольника ABCDE равен:

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

где t — это количество треугольников, а n — количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.

Источник

Геометрическая фигура многоугольник

Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.

Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.

Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.

Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.

Основные понятия

Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:

Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:

Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.

Виды фигур

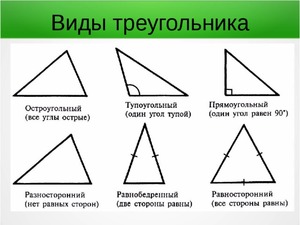
Треугольник

Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.

Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.

По соотношениям между сторонами все треугольники можно подразделять на несколько видов:

Кроме того, принято различать следующие треугольники:

Четырехугольник

Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.

На одной прямой не может находиться сразу три вершины четырехугольника.

Видео

Дополнительную информацию о многоугольниках вы найдете в этом видео.

» width=»560″ height=»314″ allowfullscreen=»allowfullscreen»>

Источник

Многоугольники

Ломаная — это геометрическая фигура, которая состоит из точек,
соединенных отрезками. Отрезки называются звеньями ломаной,
а точки называются вершинами ломаной. Сумма длин всех
звеньев называется длиной ломаной.

Замкнутая ломаная — это ломаная, у которой конец последнего
звена совпадает с началом первого звена.

Простая ломаная — это ломаная, у которой нет пересечений.

Многоугольник — это геометрическая фигура с множеством
углов и сторон, или по другому это простая замкнутая ломаная,
у которой соседние звенья не лежат на одной прямой.

Как и у любой другой геометрической фигуры, у многоугольника
есть стороны и углы. Звенья ломаной называют сторонами
многоугольника, а вершины ломаной называют углами
многоугольника. Периметр многоугольника равен сумме
длин всех сторон многоугольника, или по другому длине ломаной.

Соседние вершины многоугольника — это два угла
многоугольника,принадлежащие одной стороне.

Диагональ многоугольника — это отрезок, соединяющий
две любые не соседних угла.

Произвольный многоугольник разделяет плоскость на две части.
Одна из частей называется внутренней областью, а другая внешней
областью многоугольника. Углы, которые находятся во внутренней
области называются внутренними, соответственно углы, которые
находятся во внешней области называются внешними.

Источник

Мерзляк 5 класс — § 13. Многоугольники. Равные фигуры

Вопросы к параграфу

1. Какая фигура ограничивает многоугольник? — Замкнутая ломаная, звенья которой не пересекаются.

2. Могут ли звенья ломаной, ограничивающей многоугольник, пересекаться? — Нет, не могут.

3. Какие элементы многоугольника вы знаете? — Вершина, сторона, углы многоугольника.

4. Как называют и обозначают многоугольник? — Многоугольники называют и обозначают по его вершинам. Чтобы записать название многоугольника, надо последовательно записать все его вершины.

5. Что называют периметром многоугольника? — Периметр многоугольника — это сумма длин все его сторон.

6. Какие многоугольники называют равными? — Многоугольники называют равными, если они совпадают при наложении.

7. Какие фигуры называют равными? — Фигуры называют равными, если они совпадают при наложении.

Решаем устно

1. Сумму чисел 24 и 18 уменьшите на 33.

(24 + 18) — 33 = 42 — 33 = 9

2. Разность чисел 30 и 14 увеличьте в 3 раза.

3. Произведение чисел 12 и 5 увеличьте на 19.

(12 • 5) + 19 = 60 + 19 = 79

4. Частное чисел 189 и 9 уменьшите в 7 раз.

(189 : 9) : 7 = 21 : 7 = 3

5. Укажите среди данных отрезков равные, если:

Ответ: АВ = TQ и EF = MN.

Упражнения

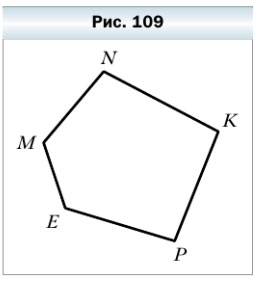
321. Назовите вершины и стороны пятиугольника, изображённого на рисунке 109.

323. Вычислите периметр пятиугольника, стороны которого равны 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.

Периметр многоугольника равен сумме длин его сторон.

2 см + 4 см + 5 см 5 мм + 6 см + 7 см = 24 см 5 мм — периметр данного пятиугольника.

324. Вычислите периметр шестиугольника, три стороны которого равны по 8 см, а три другие — по 10 см.

Периметр многоугольника равен сумме длин его сторон.

8 • 3 + 10 • 3 = 24 + 30 = 54 (см) — периметр данного шестиугольника.

325. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 110.

326. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 111.

327. Одна из сторон четырёхугольника равна 8 см, вторая сторона в 3 раза больше первой, а третья — на 7 см меньше второй и на 9 см больше четвёртой. Вычислите периметр четырёхугольника.

1) 8 • 3 = 24 (см) — длина второй стороны четырёхугольника.

2) 24 — 7 = 17 (см) — длина третьей стороны четырёхугольника.

3) 17 — 9 = 8 (см) — длина четвёртой стороны четырёхугольника.

4) 8 + 24 + 17 + 8 = 57 (см) — периметр четырёхугольника.

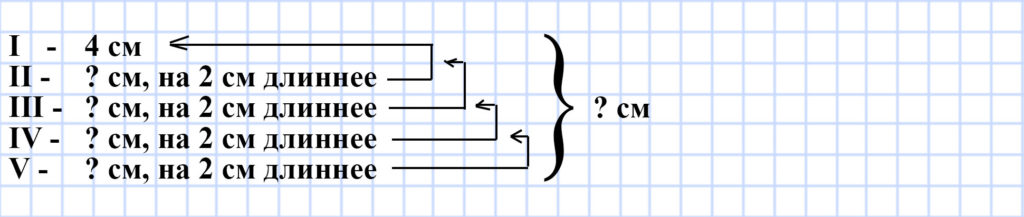
328. Стороны пятиугольника пронумеровали. Первая сторона равна 4 см, а каждая следующая сторона на 2 см длиннее предыдущей. Вычислите периметр пятиугольника.

1) 4 + 2 = 6 (см) — длина второй стороны пятиугольника.

2) 6 + 2 = 8 (см) — длина третьей стороны пятиугольника.

3) 8 + 2 = 10 (см) — длина четвёртой стороны пятиугольника.

4) 10 + 2 = 12 (см) — длина пятой стороны пятиугольника.

5) 4 + 6 + 8 + 10 + 12 = 40 (см) — периметр пятиугольника.

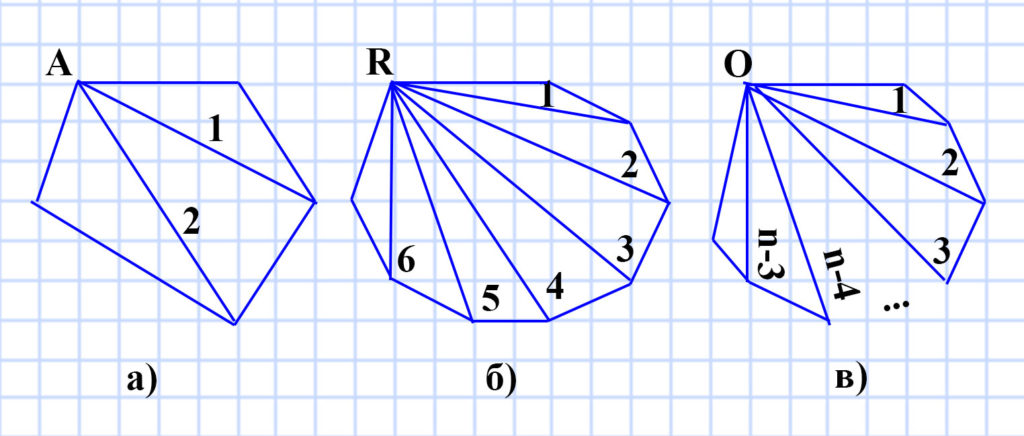
329. 1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) и-угольника, где п > 3?

а) Из одной вершины пятиугольника можно провести 2 диагонали.

б) Из одной вершины девятиугольника можно провести 6 диагоналей.

в) Из одной вершины n-угольника можно провести (n-3) диагоналей, так как:

2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике; в) в и-угольнике, где п > 3?

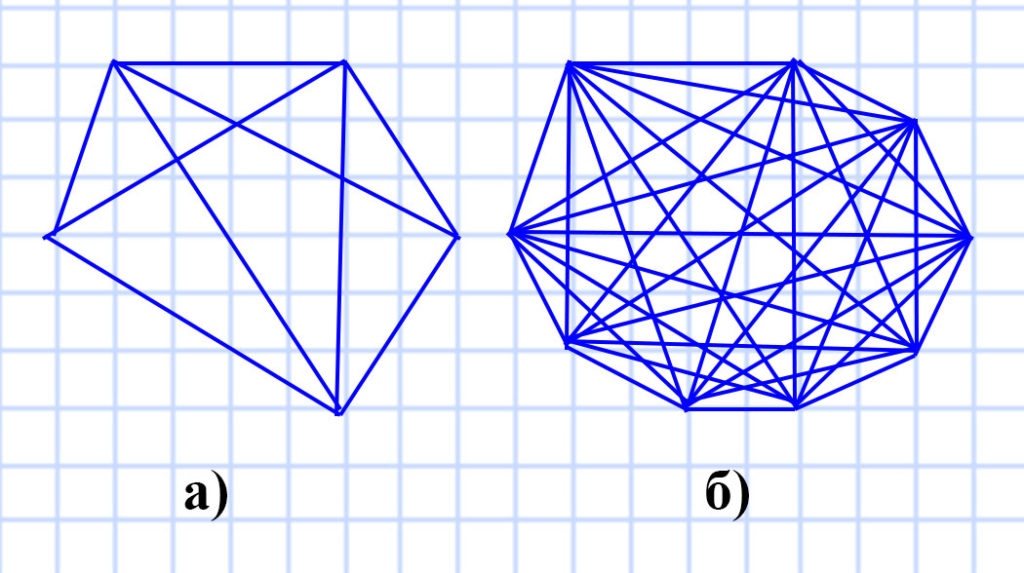
а) Мы знаем, что из одной вершины пятиугольника можно провести 2 диагонали (n-3), Значит из 5 вершин можно провести 5 • 2 = 10 диагоналей (n • (n-3)). Но если провести все 10 диагоналей, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в пятиугольнике можно провести 10 : 2 = 5 диагоналей ((n •(n-3) : 2). Рисунок подтверждает наш вывод.

б) Мы знаем, что из одной вершины девятиугольника можно провести 6 диагоналей (n-3 = 9 — 3 = 6), Значит из 9 вершин можно провести 9 • 6 = 54 диагонали (n • (n-3) = 9 • (9 — 3) = 9 • 6 = 54). Но если провести все 54 диагонали, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в девятиугольнике можно провести 54 : 2 = 27 диагоналей ((n • (n-3) : 2 = 9 • (9 — 3) : 2 = 9 • 6 : 2 = 54 : 2 = 27). Рисунок подтверждает наш вывод.

в) Исследуя предыдущие два задания мы вывели формулу, по которой можно посчитать количество возможных диагоналей в n-угольнике, при n > 3: n • (n-3) : 2. Это значит, у количество диагоналей:

Ответ: 5, 27, n • (n-3) : 2.

330. Как, используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2°?

Для того, чтобы используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2° надо:

331. Как построить угол, градусная мера которого 1°, используя шаблон угла, градусная мера которого равна:

а) 19°

Для того, чтобы используя шаблон угла, градусная мера которого 19°, построить угол, градусная мера которого равна 1° надо:

Для того, чтобы используя шаблон угла, градусная мера которого 7°, построить угол, градусная мера которого равна 1° надо:

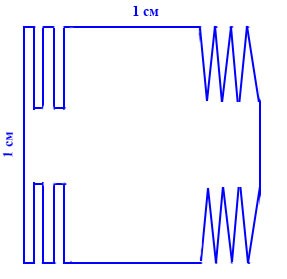
332. Существует ли многоугольник с периметром, равным 1 000 000 см, который можно целиком расположить в квадрате со стороной 1 см?

Да, теоретически такой многоугольник существует. Для этого надо из квадрата со стороной 1 см вырезать множество полосок либо треугольников, либо ещё каких-нибудь фигур вдоль нескольких сторон исходного квадрата. Точное количество таких вырезанных фигур будет зависеть от длины вырезаемых из квадрата сторон фигуры, а также от длины оставшихся от исходного квадрата сторон.

В реальности такую операцию способны выполнить только суперточные приборы, например лазерный принтер. Кроме того, необходимо провести очень точный расчёт вырезаемых фигур.

Упражнения для повторения

333. Сравните:

1) 3 986 г и 4 кг: 4 кг = 4000 г ⇒ 3 986 г

2) 6 м и 712 см: 6 м = 600 см ⇒ 600 см

3) 60 см и 602 мм: 60 см = 600 мм ⇒ 600 мм

4) 999 кг и 10 ц: 10 ц = 1000 кг ⇒ 999 кг

334. Выполните сложение, выбирая удобный порядок вычислений:

1) (636 + 927) + 364 = (636 + 364) + 927 = 1 000 + 927 = 1 927

2) (425 + 798) + 675 = (425 + 675) + 798 = 1 100 + 798 = 1 898

3) 212 + 493 + 788 + 807 = (212 + 788) + (493 + 807) = 1 000 + 1 300 = 2 300

4) 161 + 455 + 839 + 945 = (161 + 839) + (455 + 945) = 1 000 + 1 400 = 2 400

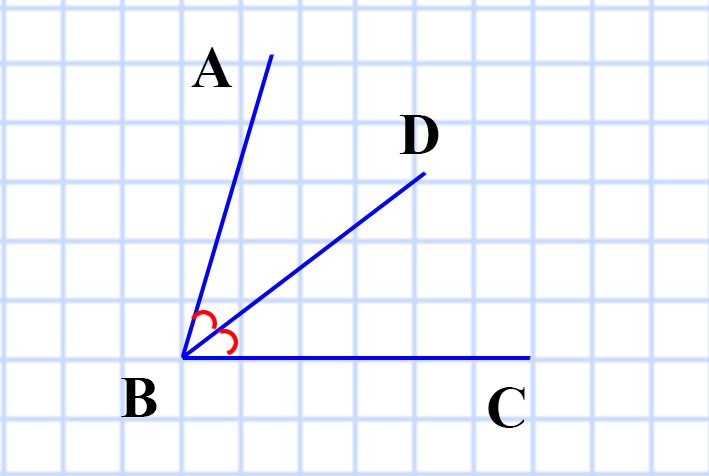
335. Известно, что ∠ABC = 74°, а луч BD — его биссектриса. Вычислите величину угла DBC.

Мы знаем, что биссектриса угла всегда делит угол пополам. Значит:

∠DBC = ∠ABC : 2 = 74° : 2 = 37°

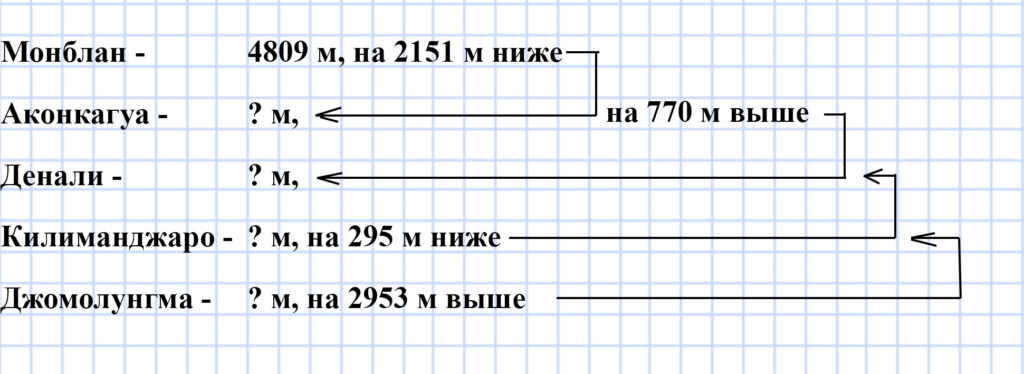
336. Высота самой высокой горы Западной Европы Монблан равна 4 809 м. Она на 2 151 м ниже самой высокой горы Южной Америки Аконкагуа, которая на 770 м выше самой высокой горы Северной Америки Денали. Какова высота самой высокой горы Африки Килиманджаро, если она на 295 м ниже горы Денали? Какова высота самой высокой горы мира Джомолунгмы (Эверест) (рис. 112), если она на 2 953 м выше горы Килиманджаро?

1) 4 809 + 2 151 = 6 960 (м) — высота горы Аконкагуа.

2) 6 960 — 770 = 6 190 (м) — высота горы Денали.

3) 6 190 — 295 = 5 895 (м) — высота горы Килиманджаро.

4) 5 895 + 2 953 = 8 848 (м) — высота горы Джомолунгма.

Ответ: 8 848 метров.

Задача от мудрой совы

337. Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?

Так как купили больше двух, но меньше семи лимонов, то количество купленных лимонов может быть либо 3, либо 4, либо 5, либо 6.

Масса каждого лимона — целое число, причём все лимоны одинаковые. Проверим, на какое из возможных чисел (3, 4, 5 или 6) общая масса покупки 850 г делится без остатка. Для этого применим метод подбора.

Под заданные условия подходит только число 5.

Источник