Касательная в геометрии что это
Окружность. Касательная к окружности.
Прямая (MN), имеющая с окружностью только одну общую точку (A), называется касательной к окружности.
Общая точка называется в этом случае точкой касания.
Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.
Теорема.
Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая — касательная.
Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B. Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.
Обратная теорема.
Если прямая касательная к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.
Следствие.
Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.
Теорема.
Касательная параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.
Пусть прямая AB касается окружности в точке M и параллельна хорде СD. Требуется доказать, что ∪CM= ∪MD.
Проведя через точку касания диаметр ME, получаем: EM ⊥ AB и следовательно, EM ⊥ СD. Поэтому СM=MD.
Через данную точку провести касательную к данной окружности.
Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.
Рассмотрим тот случай, когда точка дана вне круга.
Пусть требуется провести к окружности с центром O касательную через точку A. Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.
Следствие.
Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.
Так AD=AE и ∠OAD = ∠OAE потому, что прямоугольные треугольники AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны. Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.
Что такое касательная к окружности
Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.
Вот парочка примеров:
Окружность с центром O касается прямой l в точке A 
Из любой точки M за пределами окружности можно провести ровно две касательных 
Различие между касательной l, секущей BC и прямой m, не имеющей общих точек с окружностью
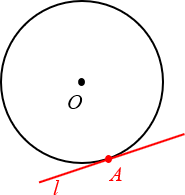
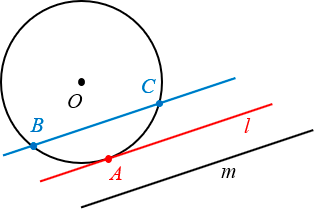
На этом можно было бы закончить, однако практика показывает, что недостаточно просто зазубрить определение — нужно научиться видеть касательные на чертежах, знать их свойства и вдобавок как следует попрактиковаться в применении этих свойств, решая реальные задачи. Всем этим всем мы сегодня и займёмся.
Основные свойства касательных
Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.
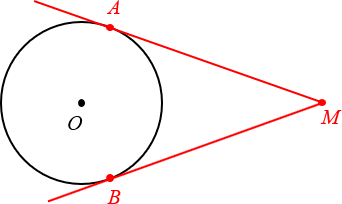
1. Отрезки касательных, проведённых из одной точки, равны
Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:
Отрезки касательных к окружности, проведённых из одной точки, равны.
Отрезки AM и BM равны
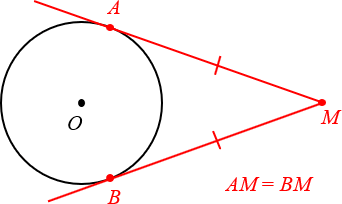
2. Касательная перпендикулярна радиусу, проведённому в точку касания
Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы OAMи OBM — прямые.
Радиус, проведённый в точку касания, перпендикулярен касательной.
Этот факт можно использовать без доказательства в любой задаче:
Радиусы, проведённые в точку касания, перпендикулярны касательным
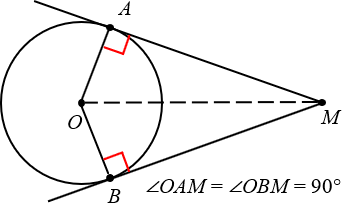
Кстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.
3. Соотношение между касательной и секущей
А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).
Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной
Соотношение между секущей и касательной
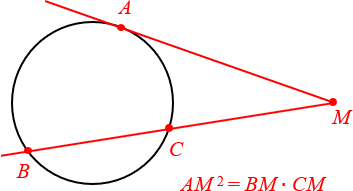
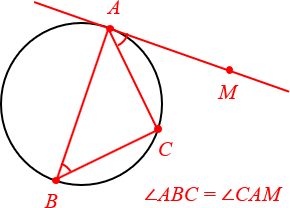
4. Угол между касательной и хордой
Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.
Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.
Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.
Иногда всё-таки касается 🙂
Касательная (геометрия)
Было бы неправильно, как это иногда делается, определить касательную как прямую, которая «касается кривой, но не пересекает ее», поскольку
Аналогом понятия касательной к поверхностям является понятие касательной плоскости. Его можно определить, рассматривая набор кривых, нарисованных на поверхности и проходящих через заданную точку, и рассматривая набор полученных касательных. Затем мы можем обобщить на объекты размерности больше 2.
Резюме
Геометрическое определение касательной
Касательная к кривой C в точке A абсциссы a является предельным положением, если оно существует, секущей линии (AB), когда точка B кривой стремится к точке A.
Пример: касательная к окружности
Угол между двумя кривыми
Рассмотрим две кривые C и C ‘, проходящие через одну и ту же точку M; предполагается, что в этой точке у них обоих есть касательные.
Расчет касательной
Касательная к числовому функциональному графу
По касательной к параметрической дуге
Связь с дифференциальным исчислением
Если f допускает последовательность нулевых производных по a, то первая ненулевая производная, идущая к порядку p
тогда идет касательная, направленная по первой ненулевой производной. В такой точке мы говорим, что существует контакт порядка p между кривой и ее касательной (в то время как в регулярной точке контакт имеет только порядок 1).
Половина касательных
Мы говорим, что имеется полукасательная вправо, когда существует следующий предел
Мы говорим, что есть полукасательная слева, когда существует следующий предел (обратите внимание на порядок)
Если есть полукасательные, мы используем следующий словарь:
График функции абсолютного значения дает пример угловой точки
В случае дельтовидной мышцы мы видим три бугорка.
Кривая в полярных координатах
Касательная для неявной кривой
Рассмотрим кривую декартовой уравнения Р (х, у) = C в евклидовой плоскости, для функции F из класса на открытой одной плоскости. ПРОТИВ 1 <\ Displaystyle <\ mathcal 
Положение относительно касательной
Выпуклость
График дифференцируемой числовой функции выпуклый тогда и только тогда, когда кривая всегда находится выше своих касательных. Она вогнута тогда и только тогда, когда кривая находится ниже своих касательных.
В тех случаях, которые встречаются на практике, кривая попеременно вогнута или выпукла на различных интервалах, разделенных точками перегиба (для которых касательная пересекает кривую).
Использование дифференциального исчисления для замечательных точек
В этом кадре дуга принимает вид ( X ( t ), Y ( t )). Затем мы выполняем ограниченное разложение функций X и Y :
Распространение на поверхности и за их пределы
Касательная в художественном рисовании
В рисовании и анимации художники стараются избегать касания двух кривых. Действительно, касание рискует нарушить эффект перспективы, поскольку мы не знаем, какая поверхность находится перед другой, с одной стороны; и, с другой стороны, прямые линии, касательные к двум кривым, образуют крест, который притягивает взгляд и не позволяет ему перемещаться по рисунку.
Касательная к окружности
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
